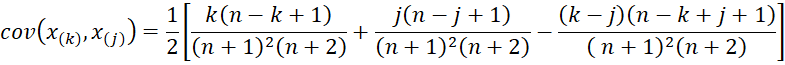Order Statistics for a Uniform Population

Basic Properties

The following properties are Properties 3 and 4 from Order Statistics from a Continuous Population.

Property 1: If the population follows the uniform distribution on the interval (0,1), the kth order statistic has a beta distribution Bet(k, n-k+1).

Property 2: If the population follows the uniform distribution on the interval (0,1), the mean and variance of the kth order statistic are

Mean and variance

E.g. the mean of the 3rd order statistic from a sample of size 10 is 3/11 = .2727. We get the same value when using the formula =ORDER_MEAN(3,10,,”uniform”,0,1). See Order Statistics from a Continuous Population.

Observation: For a sample of size n from a population with a uniform distribution on (0,1), the distribution of the kth order statistic can be expressed in Excel by

fk(x) = BETA.DIST(x,k,n-k+1,FALSE)

Fk(x) = BETA.DIST(x,k,n-k+1,TRUE)

For any continuous distribution, the cdf F(x) is an increasing function on the interval (0,1). Thus, if x1, …, xn is a sample from this distribution in increasing order, then F(x1), …, F(xn) is a sample from the uniform distribution on (0,1) and the kth order statistic from the uniform distribution is F(x(k)).

Generalization

Property 3: For any distribution with cdf F(x)

Fk(x) = BETA.DIST(F(x),k,n-k+1,TRUE)

Proof: F(x) has a uniform distribution on (0,1) and so

F(x)∼ Bet(k, n-k+1)

and the result follows from Property 1.

Observation: For example, the kth order statistic for the gamma distribution Gamma(α, β) could be calculated in Excel by the formula

Fk(x) = BETA.DIST(GAMMA.DIST(x,α,β,TRUE),k,n-k+1,TRUE)

Joint Distribution

Property 4: For a uniform distribution on (0,1) where x < y

Joint order statistic uniform

Proof: By Property 3 of Joint and Range Order Statistics from a Continuous Population

f_j,k(x,y)

Proof 1

Property 5: For a uniform distribution on (0,1)

Proof 2

Proof: Click here for the proof using calculus.

Observation: Note that the distribution of x(k) – x(j) only depends on the difference k – j. Thus, for example, the distribution of x(5) – x(2) is the same as the distribution of x(7) – x(4).

Based on Property 5, we see that the mean and variance of x(k) – x(j) are

Mean of range

Variance of range

Variance continued

Also, note that

Variance of difference

Thus

Proof 2

Solving for cov(x(k),x(j)), we get the covariance between two order statistics.

Covariance two order statistics

References

Border, K. C. (2016) Lecture 15: Order statistics; conditional expectation. Caltech
https://healy.econ.ohio-state.edu/kcb/Ma103/Notes/Lecture15.pdf

Ma D. (2010) The distribution of the order statistics. A Blog on probability and statistics
https://probabilityandstats.wordpress.com/2010/02/20/the-distributions-of-the-order-statistics/

Ma, D. (2010) The order statistics and the uniform distribution. A Blog on probability and statistics
https://probabilityandstats.wordpress.com/2010/02/21/the-order-statistics-and-the-uniform-distribution/

Leave a Comment