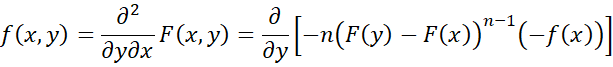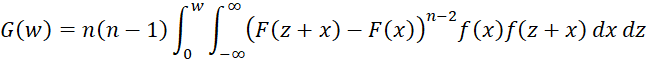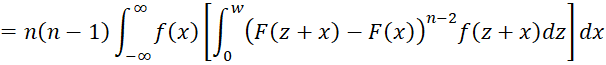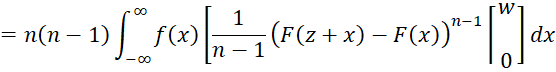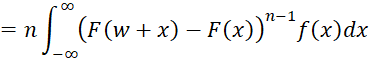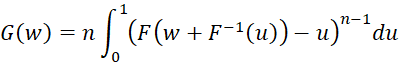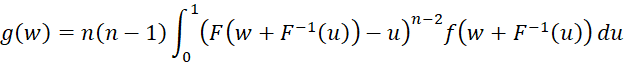Order Statistics Proofs

Order statistics from a continuous population

Property 3 of Order statistics from continuous population: The pdf of the kth order statistic is

Continuous uniform distribution pdf

Proof: We use the fact that the pdf is the derivative of the cdf.

By Property 1 of Order statistics from continuous population, the cdf of the kth order statistic is

Continuous uniform distribution cdf

Now

f(x)

We now claim that the two sums in the last expression cancel each other out, leaving only the first expression, which is the desired result. To see that the difference between the last two sums is zero, make a change of variables in the last sum by replacing i by j-1. In this way the last sum becomes

Joint order statistics from a continuous population

Property 2 from Joint Order Statistics from a Continuous Population

Let f1,n(x,y) be the joint pdf function for the first and last order statistic for a sample of size n taken from a population with cdf F(x) and pdf f(x). Then

f_1,n(x,y)

if x < y. Otherwise, f1,n(x,y) = 0.

Proof:

Property 4 proof 1

Proof part 2

Range statistics from a continuous population

Property 7 from Range Statistics from a Continuous Population

The cdf of w = x(n) – x(1) is equal to

Cdf of range statistic

Proof: By Property 5 of Range Statistics from a Continuous Population

Proof 1

Proof 2

Proof 3

Proof 4

Using the substitution u = F(x), we see that  x = F-1(u) and du = f(x)dx, and so

Change of variables

Property 6 from Range Statistics from a Continuous Population

The same change in variables for Property 5 of Range Statistics from a Continuous Population yields

Pdf change of variables

Order statistics from a uniform distribution

Property 5 from Order Statistics from a Uniform Distribution

For a uniform distribution on (0,1)

Proof 2

Proof: Assume that 0 < x < y < 1 and w = y-x. Thus, 0 < x < w+x < 1. Using the fact that y = w+x, by Property 4 of Order Statistics from a Uniform Distribution and Property 5 from Range Statistics from a Continuous Population, we see that the pdf g(w) of x(k) – x(j) is

Proof 1

Property 2

We now use the substitution x = z(1-w) and so dx = (1-w)dz and z = 1 when x = 1-w

Proof 3

Proof 4

Proof 5

Thus

Proof 6

But

Proof 7

Hence

Proof 8

Proof 9

Proof 10

Proof 11

which is the pdf of Bet(k-j, n-(k-j)+1).

References

David, H. A. and Nagaraja, H. N. (2003) Order statistics. Wiley
https://books.google.it/books/about/Order_Statistics.html?id=3Ts1yDLWXmQC&redir_esc=y

Omondi, O. C. (2016) Order statistics of uniform, logistic and exponential distributions
http://erepository.uonbi.ac.ke/bitstream/handle/11295/97307/MSc_Project2016.pdf?sequence=1&isAllowed=y

Arnold, B. C., Balakrishnan, N., Nagaraja, H. N. (2003) A First course in order statistics. Society for Industrial and Applied Mathematics
https://books.google.it/books/about/A_First_Course_in_Order_Statistics.html?id=gUD-S8USlDwC&redir_esc=y

Ma D. (2010) The distribution of the order statistics. A Blog on probability and statistics
https://probabilityandstats.wordpress.com/2010/02/20/the-distributions-of-the-order-statistics/

Border, K. C. (2016) Lecture 15: Order statistics; conditional expectation. Caltech
https://healy.econ.ohio-state.edu/kcb/Ma103/Notes/Lecture15.pdf

Rundel, C. (2012) Lecture 15: order statistics. Duke University
No longer available online

Leave a Comment