Objective
Order statistics are used for many purposes, including reliability, outlier detection, quality control, disaster planning, and goodness-of-fit testing. We present three examples on this webpage.
Reliability
Example 1: The time to failure for a sophisticated component follows a Weibull distribution with α = 800 and β = .7. What is the probability that the component will last more than 1,000 hours?
The probability is 31.066% using the formula
=1-WEIBULL.DIST(1000,.7,800,TRUE)
Suppose that a system that you are building uses 5 of these components. If any one of these fails, then the system will fail. The probability that the first order statistic is less than or equal to 1,000 is .9971065, as calculated by
=ORDER_DIST(1000,1,5,,”weibull”,.7,800)
This is the probability that the smallest time to failure of the 5 components is less than or equal to 2000. Thus, the probability that the system will last more than 1,000 hours is .28935%, which of course is (31.066%)5.
The engineering team modified the system so that the system would still function provided no more than 1 component fails. What is the probability that the system will last more than 1,000 hours? The probability is
=1-ORDER_DIST(1000,2,5,,”weibull”,.7,800)
which is 3.4996%.
In the above, we have assumed that the failure of any one component is independent of the others.
Outliers Detection
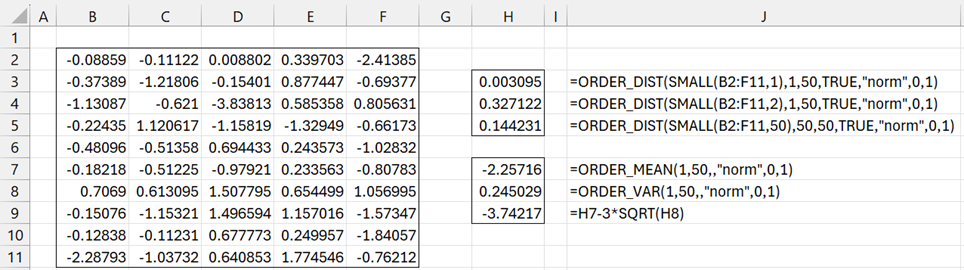
Example 2: Which of the elements from the sample of size 50 from a standard normal distribution shown in Figure 1 is likely to be an outlier?
Figure 1 – Outlier Detection
We see that the probability that the smallest element in a sample of size 50 is less than or equal to the actual smallest element in the sample, namely -3.83813 is 0.3095% (cell H4), which seems pretty unlikely. Thus this evidence that -3.83813 is an outlier
Note too that the mean for the smallest element in a sample of size 50 is –2.25716 (cell H7), and in fact a mean 3 standard deviations below the expected value is -374217 (cell H9) is still higher than -3.83813, further confirming that this is an outlier.
The probability that the second smallest element in a sample of size 50 is less than or equal to the actual second smallest element in the sample, namely -2.28793 is 32.7122% (cell H5). Thus, -2.28793 is not an outlier.
The probability that the largest element in a sample of size 50 is greater than or equal to the actual largest element in the sample, namely 1.774546 is 14.4231% (cell H6). Thus, 1.774546 is not an outlier.
Quality Control
Example 3: A company making candies suspected there was a quality control problem. The weight of each candy is supposed to be 5 grams with a standard deviation of .01. They decided to take the weights of a sample of 25 candies. Based on the data shown in Figure 2, determine whether there is a quality problem.
Figure 2 – Quality Control
The range of the sample is .090893 (cell I4). The probability of a range this high or higher is 1.6667% (cell I6). The quality control engineer decided to investigate the production line.
Also note that the expected range is .045143, as calculated by
=ORDER_MEAN(50,50,,”norm”,5,0.01)-ORDER_MEAN(1,50,,”norm”,5,0.01)
This about half of the observed value.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Arnold, B. C., Balakrishnan, N., Nakaraja, H. N. (2008) A first course in order statistics. Siam
https://books.google.it/books?id=dVP-RTea5wcC&printsec=frontcover#v=onepage&q&f=false