If we take a sample of size n from a continuous population, the kth order statistic is the kth smallest element in the sample. If we assume that the order of the elements in the sample is x1 ≤ x2 ≤ … ≤ xn, then the kth order statistic, denoted x(k) is xk. Just as the mean can be treated as a random variable, we will also use the notation x(k) to represent a random variable.
CDF of the kth order statistic
Suppose that the population has a continuous distribution with cdf F(u). We describe the (cumulative) distribution Fk(x) of the kth order statistic in a sample of size n taken from the population.
Property 1: The cdf of the kth order statistic in the sample is
Proof:
The probability that i elements in the sample are less than or equal to x is equivalent to tossing a coin n times and getting i heads where the probability of heads on any toss is F(x). Using the binomial distribution this is C(n,i)F(x)n[1-F(x)]n-i, which completes the proof.
Special cases
If n is odd so that n = 2k+1, the cdf of the kth order statistic (the median) in the sample is
The cdf of the nth-order statistic is
Alternatively,
Similarly, the cdf of the first-order statistic
Using algebra, we see that the inverse functions for the first- and last-order statistics are:
Beta distribution characterization
We can express the cdf of the kth order statistic more simply based on the following property. This property is explained in Order Statistics for a Uniform Distribution.
Property 2: For any distribution with cdf F(x)
F(x)∼ Bet(k, n-k+1)
and so
Fk(x) = BETA.DIST(F(x),k,n-k+1,TRUE)
For example, the kth order statistic for the gamma distribution Gamma(α, β) could be calculated in Excel by the formula
Fk(x) = BETA.DIST(GAMMA.DIST(x,α,β,TRUE),k,n-k+1,TRUE)
Inverse of the CDF
Since
F(x)∼ Bet(k, n-k+1)
Now suppose
Fk(x) = p
Thus
G-1(p) = F(x)
where G(x) is the cdf for the beta distribution Bet(k, n-k+1). It now follows that
x = F-1(G-1(p))
As we noted above, the kth order statistic for the gamma distribution Gamma(α, β) can be calculated in Excel by the formula
Fk(x) = BETA.DIST(GAMMA.DIST(x,α,β,TRUE),k,n-k+1,TRUE)
Thus, the inverse can be calculated in Excel by the formula
Fk-1(p) = GAMMA.INV(BETA.DIST(p,n-k+1),α,β)
The same is true for any distribution, not just the gamma distribution.
PDF of the kth order statistic
Suppose that the population has a continuous distribution with pdf f(u) and cdf F(u). We describe the probability density function fk(x) of the kth order statistic in a sample of size n taken from the population.
Property 3: The pdf of the kth order statistic is
Proof: Click here for the proof.
Special cases
Suppose n is an odd number where n = 2k – 1 then the pdf of the median can be expressed as
Mean and variance of the kth order statistic
Property 4: The mean μk of the kth order statistic for a sample of size n can be expressed as
Here Area0≤x≤1h(x) is the area under curve y = h(x) bounded by x = 0, x = 1 and the x axis. For those of you familiar with calculus, this can be expressed as
Property 5: The variance of the kth order statistic for a sample of size n can be expressed as
where
or using calculus
Approximate Values
The mean μk and variance of the kth order statistic for a sample of size n from a distribution with pdf f(x) and cdf F(x) can be estimated by
where p = k/(n+1).
The accuracy of these estimates varies widely. The estimates are exact for a uniform distribution.
Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack supports the following worksheet functions. These functions refer to a distribution dist (“uniform”, “normal”, etc.) with the specified parameters as described for the MEAN_DIST and VAR_DIST functions (see Distribution Property Functions).
ORDER_DIST(x, k, n, cum, dist, param1, param2, param3) = the pdf f(x) for the kth order statistic from a sample of size n for the specified distribution if cum = FALSE and the corresponding cdf F(x) if cum = TRUE.
ORDER_INV(p, k, n, dist, param1, param2, param3) = the inverse at p for the kth order statistic from a sample of size n for the specified distribution; i.e. the value x such that F(x) = p.
ORDER_MEAN(k, n, iter, dist, param1, param2, param3) = the expected value of the kth order statistic from a sample of size n for the specified distribution.
ORDER_VAR(k, n, iter, dist, param1, param2, param3) = the variance of the kth order statistic from a sample of size n for the specified distribution.
iter = # of intervals used to calculate the integral (default 1000).
Examples
For example, =ORDER_DIST(7,5,11,TRUE,”laplace”,10,5) takes the value .1576. Thus for a random sample of size 11 taken from the Laplace distribution with mu = 10 and beta = 5, the cdf F5(7) = .157588 for the 5th order statistic. This means that the probability that the 5th order statistic from a sample of size 11 from the specified Laplace distribution is less than or equal to 7 is 15.7588%.
Thus, =ORDER_INV(.157588,5,11,”laplace”,10,5) takes the value 7. Note, however, that =ORDER_INV(.1576,5,11,”laplace”,10,5) takes the value 7.000117.
The value of =ORDER_MEAN(6,11,,”laplace”,10,5) is 10. This means that the expected value for the median, i.e. the 6th order statistic, of the Laplace distribution with μ = 10 and β = 5 is 10. This is as expected since in general μ is the median of a Laplace distribution.
Simulation
We simulate a sample of size 1,000 from the 6th order statistic from a sample of size 11 for a Laplace distribution with mu = 10 and beta = 5. We do this by inserting the formula =ORDER_INV(RAND(), 6, 11,”laplace”, 10, 5) in cell A1, highlight range A1:J100, and press Ctrl-R and Ctrl-D. The first 8 rows are shown on the left side of Figure 1.
Figure 1 – Simulation Mean and Variance
The mean of this sample is 9.968 as shown in cell M2 and the variance is 3.449 as shown in cell M5. These simulated values are pretty close to the values calculated by the ORDER_MEAN and ORDER_VAR formulas shown in cells M3 and M6.
Normal Distribution
An estimate for the mean of the kth order statistic for a sample of size n from a normal distribution is given by
where α = π/8. In Excel, we have
μk = μ+σ*NORM.S.INV((k-Pi()/8)/(n-Pi()/4+1))
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Chen, P-N (2008) Basic theories on order statistics
Reference no longer available
Omondi, O. C. (2016) Order statistics of uniform, logistic and exponential distributions
http://erepository.uonbi.ac.ke/bitstream/handle/11295/97307/MSc_Project2016.pdf?sequence=1&isAllowed=y
Ma D. (2010) The distribution of the order statistics. A Blog on probability and statistics
https://probabilityandstats.wordpress.com/2010/02/20/the-distributions-of-the-order-statistics/
Border, K. C. (2016) Lecture 15: Order statistics; conditional expectation. Caltech
https://healy.econ.ohio-state.edu/kcb/Ma103/Notes/Lecture15.pdf
Stack Exchange (2015) Approximate order statistics for normal random variables
https://stats.stackexchange.com/questions/9001/approximate-order-statistics-for-normal-random-variables
Royston, J. P. (1982) Expected normal order statistics (exact and approximate)
https://gwern.net/doc/statistics/order/1982-royston.pdf
Baglivo, J. O. (2004) Mathematica laboratories for mathematical statistics. ASA-SIAM
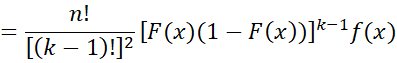
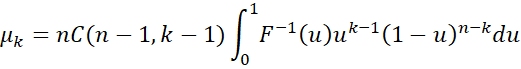
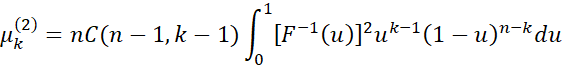
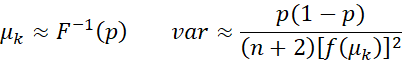

Thank you Chares. Both your site and personal insight have always been extremely valuable.
Hi Charles, your treatment of order statistics was quite revealing compared to other sites, so I was wondering if you could show the formula for the variance of the kth order statistic for n samples from a normal parent distribution? This is important when estimating the error of a percentile value PV where I = 0.025*N+0.5 and PV = Sorted Value(I) from a Monte Carlo simulation. When P is an integer, its variance is the variance of the Order Statistic I.
Thanks.
Hi Bruce,
Is the following article helpful for your purposes?
https://stats.stackexchange.com/questions/394960/variance-of-normal-order-statistics
Charles