Basic Concepts
We now describe repeated-measures ANOVA with one within-subjects factor and no between-subjects factors. Examples of this type of analysis are:
- A study is made of 10 subjects each of whom is asked to take a test on reading comprehension, mathematical ability and knowledge of history
- Research is conducted of 10 married couples, and the husband’s IQ is compared with his wife’s
- A study is made of 10 monkeys, each of whom is given training once a week for 5 weeks with their score recorded each week
The important characteristic of each of these examples is that the treatments are not independent of each other. The most common of these analyses is to compare the results of a treatment given over a period of time to each of the participants (as for the last example above).
Excel implementation
For the version of ANOVA with repeated measures with one within-subjects factor, we can use Excel’s Two Factor ANOVA without Replication data analysis tool. Essentially the following meanings are given to the terms in Definition 2 of Two Factor ANOVA without Replication: MSRow = MSA and MSCol = MSB and similarly for df and SS. The column terms (representing the within-subjects factor) are the ones that are of interest. The row terms represent the subjects.
Since the same subject is involved, the different treatments are not independent of each other. This results in an additional assumption called sphericity, which is described in Sphericity.
Example
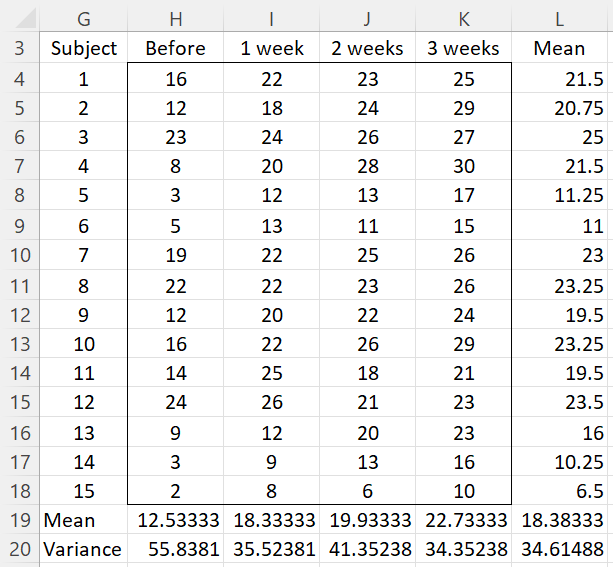
Example 1: A program has been developed to reduce the levels of stress for working women. In order to determine whether the program is successful a sample of 15 women was selected and their level of stress was measured (low scores indicate higher levels of stress) before the program, as well as 1, 2 and 3 weeks after the beginning of the program. Based on the data in Figure 1 (range G3:K18) determine whether the program is effective in reducing stress.
Figure 1 – Data for Example 1
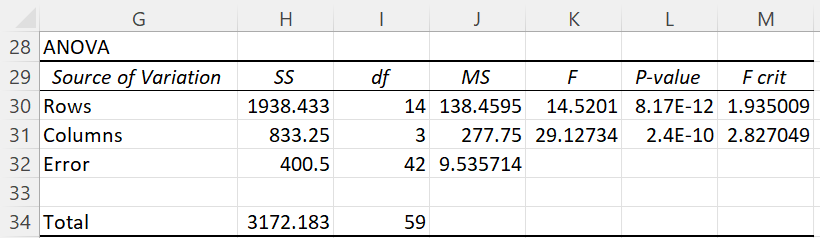
We use Excel’s Anova: Two-Factor Without Replication data analysis tool (Figure 2) to carry out the analysis.
Figure 2 – Output from Anova: Two Factor Without Replication
For this example, we aren’t interested in the analysis of the rows, only the columns, which correspond to variations by time. Since the test statistic F = 29.13 > 2.83 = F-crit (or p-value = 2.4E-10 < .05 = α), we reject the null hypothesis, and conclude there are significant difference between the means.
As usual, we can do further analysis to discover where the differences are, and so in this way determine whether the program is effective. These correspond to the planned and unplanned comparison tests for one-way ANOVA.
Contrasts
Example 2: Compare treatment means before and after the program for the data in Example 1. Determine whether the program is effective and determine the effect size.
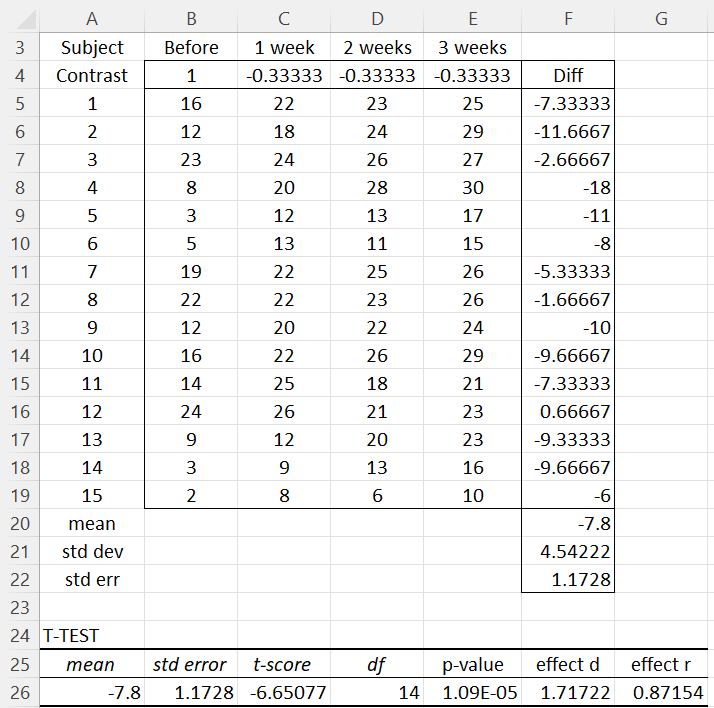
We use an approach similar to that used with independent treatments using the contrast weights (1, -1/3, -1/3, -1/3). This time, though, we calculate the standard deviation in a fashion similar to that employed for paired data as described in Paired Sample t-Test. We use the contrast weights to compute the equivalent of the differences between the paired data, and then compute the mean and standard deviation of these differences. The standard error of the means is then the standard deviation divided by . This analysis is presented in Figure 3.
Figure 3 – t-test on contrast for Example 2
Since p < .05, we conclude that there is a significant difference between stress before and after the program, and so the program appears to be effective.
Some representative formulas in Figure 3 are given in Figure 4.
Figure 4 – Representative formulas for Figure 3
If you conduct multiple contrast analyses, you need to adjust the alpha value, e.g. by using a Bonferroni or Dunn-Sidák correction as described in Planned Comparisons for ANOVA.
Standard Error for Contrasts
We could have used the MSE value from cell J32 of Figure 1 to calculate the standard error. This approach provides more power when the sphericity requirement is met and the contrast involves all the treatment levels.
Since the sphericity requirement is not met for Example 2 (see Sphericity for details), we decided to use the approach described above instead.
If we had used MSE to calculate the standard error, we would have inserted the formula =SQRT(SUMSQ(B4:E4)*MSWF(B5:E19,1)) in cell F21. The standard error would now be 0.90662 and the result would still be significant.
Effect Size
The (Cohen’s) effect size d for this contrast (cell F26 in Figure 3) is
The effect size r for this contrast is
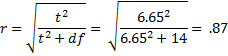
Writing up the results
We can summarize the results of this analysis as follows:
To investigate the effects of a stress reduction program therapy for working women, the stress levels of 15 participants were taken before the program and then 1, 2 and 3 weeks after the start of the program. The overall variance for repeated measures showed a significant difference between weeks (F(3, 42) = 29.13, p < .05). The mean level of stress before the program was 12.53, which increased to a mean of 22.73 three weeks after the start of the program (higher measures indicate lower levels of stress), a difference of 10.20.
A contrast on this difference was significant (t(14) = -6.65, p < .05). Using the standard deviation of contrast differences for each participant yielded an effect size of d = 1.17, showing the importance of the program in treating stress.
Post-hoc testing
For pairwise unplanned tests, contrasts can be used adjusting the alpha value using a Bonferroni or Dunn-Sidák correction if necessary. The Tukey’s HSD (for pairwise comparisons) or Scheffé test (for compound comparisons) can also be used.
For Tukey’s HSD, we use the test statistic
where s.e. is the pairwise standard error (as was done for Example 2) and not . The critical value of the studentized range q is based on the values of α, a (the number of treatments) and df = n – 1 .
For the Scheffé test, we again don’t use MSE to compute the standard error and instead of using dfB * F.INV(α, dfB, dfW) as the critical value, we use (a – 1) * F.INV(α, a – 1, n – 1).
See Repeated Measures ANOVA Tool for more details about follow-up tests after a significant Repeated Measures ANOVA.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Howell, D. C. (2010) Statistical methods for psychology (7th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf

Hello,
I’m not sure if I should use a one-way ANOVA with repeated measures for my data. I want to know if there’s a significant difference of weight between four people, let’s call them P1, P2, P3, and P4. I measured their weight over time (Day 1, Day 2, Day 3. etc).
In your first example (levels of stress for working women), the “subject” corresponds to the rows, and the week corresponds to the column, which is what you want to analyze. However, with my data, I want to analyze the four subjects (P1, P2, P3 and P4), so should I do the opposite of what you did, and place the subject for the columns and time/days for the rows ?
Did I select the right type of ANOVA, meaning one-way ANOVA with repeated measures or two factor ANOVA without replication ?
Thanks
Hello Faye,
Does your sample consist of only the 4 subjects P1, P2, P3, P4? Thus there is only one row.
What does significant difference mean in this case?
Charles
Yes, I only have 4 subjects. Why would I have only one row ?
When I said significant difference, I meant the average weight of one person over the whole sampling period (30 days). I want to see if the mean of P1 is equal to the mean of P2, P3, and P4. All four people have a measure for the 30 days (30 measures per person).
Faye,
Since you are only comparing the means for four people P1, P2, P3, P4, no statistical analysis is necessary. Just calculate the mean for each of the 4 people over the 30 days and compare the numbers. E.g. suppose the means for P1, P2, P3, P4 are 34, 26, 37, 32. Then P3 would have the highest mean and P2 the lowest. Clearly the means are different. There is no concept of “significant” difference.
Charles
Hello Charles,
Regarding the calculation of effect r under the planned comparisons test; as you have explained on the website uses the t-statistic and the degrees of freedom, yet the Real Statistics Data Analysis tool, uses the mean to calculate effect r. For instance using the above example r=sqrt(6.65^2/(6.65^2+14)) but on the Real Stats Analysis tool, effect r is calculated using -7.8. Could this be an error?
Once again thank you for creating this website. It’s an amazing learning tool.
Betty.
Hello Betty,
Yes, there is an error in the Real Statistics software. The value for r should be .87 as shown on the website. I am planning to issue a big release this weekend, Rel 8.6.3. I plan to correct this error in that release.
Thank you very much for identifying this error.
Charles
Hi Charles,
I am done with my project and I need to consult you regards my data analysis.
I have 40 participants divided to 2 groups and two balance devices were used and two outcome measures (OLST & SEBT). The OLST was tested pre-test and post-test for two (eyes opened and eyes closed, and the SEBT was tested for three reaches (ant, posteriolat, and posteriomed). The participants assigned for the balance device randomly by throwing a coin so each participants practiced a balance -training program for 6 weeks/ twice per week on one of the balance devices.
MY null hypothesis was no difference exist between pre-test and post-test for the OLST & SEBT.
research hypothesis difference exist.
Q1:Is my study design will be a repeated measures design?
Q2: Are both “two way ANOVA & repeated measures ANOVA” correct for analyzing the data?
Huda,
It depends on what you mean by “My null hypothesis was no difference exist between pre-test and post-test for the OLST & SEBT.” If you mean that (1) there is no difference between pre-test and post-test for the OLST” and (2) there is no difference between pre-test and post-test for the SEBT”, then you can perform a simple repeated measures ANOVA for (1) and another repeated measures ANOVA for (2). Alternatively, you can performed a repeated measures MANOVA (actually Hotelling’s T-Square) combining both (1) and (2)
If you are interested in comparing the differences pre- and post- for OLST with the differences pre- and post- for SEBT, then you need to perform a t test between differences for OLST with those for SEBT.
If you want to perform both of these analyses together then you can perform a repeated measures ANOVA with one within subjects factor (Time: pre- and post-) and one between subjects factor (OLST and SEBT).
I don’t understand how ant, posteriolat and posteriomed for SEBT maps into pre- and post- though.
Charles
Dear Charles
Greatly appreciate your help.
So after the application of same, I found my results to be statistically significant. But to find the possibility of any error, I applied sphericity over my data (as I had 6 column or level of data). My resultant variances were: 41.80098684, 50.53685238, 24.58650288, 66.58100329, 90.07658306, 74.15424548, 78.00806949, 87.49126234 171.9032689, 73.87541118, 48.35757607, 72.4452611, 116.5992496, 109.8337274, 68.70528372.
Can you please tell me as to what to infer from it.
Thanks
Neha,
Doesn’t seem too bad, although the 24.5865 value is a little different from the others. In any case, I would simply apply the GG epsilon and HF epsilon corrections as described on the website to see how it affects the p-value.
Charles
Dear Charles
Thank you for your reply. So as per your suggestion, I can use two factor ANOVA without replication within excel to do Single factor Repeated Measures ANOVA (as written in the aforementioned article).
Yes
Dear Charles
The link you provided still provides results for pre and post training.
Please consider that my data has no such distinction. If we were to consider in terms of factors, I have only one factor i.e. channel-set (classifier type cannot be considered as a factor) having 6 levels. So please tell me which ANOVA would fit best.
Thanks
Neha,
If you have only one factor, Single Factor ANOVA could be a good choice if the channel-sets have distinct subjects, while Single Factor Repeated Measures ANOVA could be a good choice if each subject experiences all 6 channels.
Charles
Dear Charles
let me paraphrase…I have accuracy results from 6 channel sets using 3 different classifiers. So if we consider channel set as a factor, it has 6 different levels or combinations. Similarly for the type of classifier, it has 3 levels (SVm, kNN and QDA). Each level has a resultant in the form of a numeric value for each subject (20).
What I am asking is that should I take all channel sets per classifier (20*6) or all classifiers per channel set (20*3) as a single entity for p-value calculation using ‘2-factor ANOVA without replication’ or not??
Hope its clear now.
Neha,
From your various comments, I understand that you have 20 subjects and each subject has 18 measurements, one for each of 3 classifiers and one for each of 6 channel sets. Perhaps you can analyze your data as described at https://real-statistics.com/anova-repeated-measures/two-within-subjects-factors/
Charles
Dear Charles
What about the first part. Kindly help.
Neha,
I am probably quite slow, but I still don’t understand it.
Charles
Dear Charles
Please consider channel set (a combination of channels) in place of channels wherever I have mentioned in my previous reply.
Relating to that, my null hypotheses assume that accuracy achieved from each channel set is random and highest average accuracy achieved has no statistical significance.
I want to use ANOVA to counter this argument.
Also I have another question (unrelated to aforementioned)…..will the p-value change if we change the order of the columns, say in your example of stress analysis?
Neha,
The p-value shouldn’t probably change if the order of the columns change, but this may depend on the test you are using.
Charles
Hello Charles
1. is correct.
2. 3 classifiers and 6 channels are separate so I have a total of 18 combinations i.e. applying each classifier to each of the channel combination.
3. Yes, each subject experience each one of these. The score is in the form of accuracy meaning what is the accuracy for each channel when used with each classifier ( a numeric value)
4. I want to test that the average results achieved citing the accuracy of one channel is better than all others is statistically significant or not….
Neha,
Thanks for your clarifications. Unfortunately, I don’t understand your null hypothesis (item 4).
Charles
Hello again
Let me try to explain again. I have results from 6 different channel combinations, out of which I was claiming one to be most optimal. I have done the same i.e. created these 6 channel combinations from 3 different classifiers (to identify whether the results are classifier dependent or not). The results were not classifier dependent as optimal results were obtained from the same channel set for the case of all 3 classifiers.
Now I want to analyse whether my results are statistically significant or not. As per my understanding, I should apply ANOVA to results obtained for 6 channel combination (20*6 as 20 is the number of participants) using one classifier at a time. In that way, I’ll have to apply ANOVA thrice to ensure that the results are significant for all 3 classifiers or not.
Hope you understand my problem now. If so, please confirm whether I am thinking in the correct direction.
Thanks in advance
Neha,
Sorry, but I still don’t really understand the situation. I understand the following:
1. You have 20 subjects (participants)
2. There are 3 classifiers, each of which can be subcategorized in some way into 6 channels (for a total of 18 channels? or are the same 6 channels used for each of the 3 classifiers’)
3. I presume that each subject experiences each of the 18? classifier/channels, and some score is given for each. Is this correct? Is the score a numeric value or a categorical value (if so, how many categories are there? are they ordered?)
4. What hypotheses do you want to test?
Charles
Hello Charles
I want to test whether there is any significant difference in classification accuracy within channel sets. So can I use all the channel sets as columns for my ANOVA while N subjects being the rows for ANOVA??????
Neha,
I don’t understand the scenario that you are describing, and so I am unable to answer your question.
Charles
Hello there!
I have N subject set with two independent factors as channel set and type of classifier. I want to know if I can use both the factors within a single repeated measure ANOVA (as group is same for each condition) or do I need to separately analyse them??
Neha,
This depends on what hypotheses you are trying to test by using repeated measures ANOVA.
Charles
Dear Charles
I want to use repeated measure ANOVA for a statistical measure of the classification accuracies(CA) achieved from different classifiers and channel set for the same subject set (group). Kindly explain, should I use all within a single go (CA as a column vector for each classifier and channel set) or should I do it with two columns at a time??
Neha,
I don’t have enough information to be able to answer your question.
Charles
Hello there
Please tell me what does ‘3’, ’42’ and ’14’ mean within the term F(3, 42) and t(14) respectively….
Neha,
These values are called “degrees of freedom.” They are parameters in the F and t distributions.
Charles
Thanks for your reply Mr Charles
‘3’ and ’14’ are somewhat understandable. But what is the statistical meaning of ’42’.
Why would a simple product of degrees of freedom of row and column will define degree of freedom??
Neha,
It is just the way the mathematics works. See
https://real-statistics.com/two-way-anova/two-factor-anova-without-replication/
Charles
Dear Charles
Thank you so much for making me understand the basic concepts.
I feel obliged. 🙂
Dear Charles,
I have 7 groups of different sizes (5-8), and measurements taken at baseline and four other time points. I want to see 1) if different groups respond differently at a particular time point and 2) if the response within a group differs over time. I am not sure whether I should use two-way ANOVA (time v.s. group) or repeated measures one-way ANOVA for statistical comparisons. What would you recommend? Thanks a lot!
Tiffany
Tiffany,
If the measurements at the baseline and 4 different times are taken on the same subject, then you should use repeated measures ANOVA. Since your subjects are divided into 7 different groups, you need the two-way version, what I have also called repeated measures ANOVA with one within subjects factor and one between subjects factor.
Charles
Hi Charles
I have 3 groups with unequal size assessed at baseline and after 3 months (same subjects assessed at 2 time points). There’s a clear difference for one group at the second time point (I want to show that the subjects react differently at the second time point). if I run a 2-way ANOVA with subjects as repeated measure (or not) the time is significant but the interaction is not so I can’t compare all cells?! If i run a 1 way ANOVA at baseline there’s nothing significant but 1 way ANOVA at the second time is significant due to one group. If I run paired 2-test it’s also significant for one group. If the 3 groups are similar at baseline (1 way ANOVA) then can I just run paired t-test or shall I use another statistics?
Thanks
Teddy,
When you say that you “want to show that the subjects react differently at the second time point”, do you want to show this (1) for each of the three groups or (2) for all the groups together. If (2), then simply run a one-way repeated measures ANOVA and if there is a significant result, use one of the follow up tests described on the website. You can run three separate paired t-tests, but this will increase your experiment-wise error from .05 to (1-.05)^3 = .14 (which is not great, or alternatively, you will need to reduce your alpha value to .017 with the loss of statistical power).
If (1), then you should use the testing approach described on the referenced webpage.
Hello!
I have a question. Say we are determining the number of plate cells affected by certain antibiotic dose i.e. Dose escalation. We are running 5 different antibiotic dosages (5 numerically set dosages, all inserted into plates at the same time, 90 minutes later, all cells affected will be recorded). The experiment is run 3 times, providing 3 count results per dosage.
1. I would like to first compare the difference between the results of dosages i.e. Significanct difference between dosages. Would I just use a randomized complete block ANOVA test?
2. Secondly I would like determine standard error/or error involved in reproducibility of each run at a single dose (meaning at dose 0.1, I would like to compare the number of cells affected from the runs called count 1, 2, and 3). Which equations would you recommend?
3. Lastly, let’s assume this experiment is run ANOTHER two times (each time involving the same 5 standard dosages, run 3 times as previous) . Should I calculate the mean of cells affected at each dosage? Meaning in exp1 at dosage 0.1, should I calculate the cell response mean (mean of count 1,2,3 at dosage 0.1), and in exp 2 with dosage 0.1 also find the mean of cell response (count 1,2,3) and similarly for experiment 3? And then compare the means Exp1Mean0.1, Exp2Mean0.1, Exp3Mean0.1 in order to determine the variability between the three, if a overall confidence interval per dosage, the final cumulative error value associate per dose? Should I use FOLLOW UP ANAYSIS Two Factor ANOVA. Or the simple effect of Single ANOVA?
Getting a bit confused, and could really use your help!
Thank you sir!
-NR
NB,
Sorry for the delay in responding to you.
1. I can’t tell from the information that you have provided whether a randomized complete block design is necessary or whether a randomized complete design would suffice. Are there 5 plates, one for each dosage, or is there some other configuration?
See the following webpages for more information:
https://real-statistics.com/design-of-experiments/completely-randomized-design/
https://real-statistics.com/design-of-experiments/completely-randomized-design/randomized-complete-block-design/
2 and 3. I don’t understand the scenario that you are describing well enough to be able to respond.
Charles
Dear Sir, I like your website so much.
My question is …
I want to test the image quality database.
I have images name I1, I2, I3,….I20 and it quality is varying along the three levels 0 to 10 variation mixed [for example, low (near 1, say), fair and good (towards 10, say) ]
The number of subject who is rating all the images in the scale of 1 to 10 is 50. so my data size is 20×50 (images x subject). All this data is in continuous.
My question is whether can I use ANOVA with Repeated Measures Within Subjects? If yes, then how? if No then which measure I should use?
Please explain me the steps.
Thanks
Jay,
You might be able to use ANOVA with Repeated Measures, but which test to use really depends on what you are trying to accomplish. What is your objective? What hypothesis are you trying to prove or gain eveidence for (or against)? Are you trying to get a measure of agreement between the raters?
Charles
Thank you so much for the reply sir.
Yes sir, I want to get a measure of agreement between the raters? or the association between the raters.
2) I have mean of the observation and I want to check the relation between each rater and the mean of the observation of all the rater.
Thanks in advanced.
Hi Charles
I love your website and your software!
For the Scheffe calculation, what are “a” and “n” in:
(a – 1) * FINV(α, a – 1, n – 1)?
Is a = number of groups? If so, would a – 1 = 0 in a one-way repeated measures contrast?
Is n the total sample size or a group sample size?
Nick,
Glad you like the website and software.
I don’t know where you see the formula (a – 1) * FINV(α, a – 1, n – 1), but in any case, please look at the following webpage:
Unplanned Comparisons
Charles
Hello,
I want to analyze the relationship between air pollutant levels between the inital week where no plants were introduced to the first, second, third, and fourth week where plants were introduced. I measured the data three times during the day, one a week. So my data was inputted as the columns being: the initial, week 1, week 2, week 3, and week 4 and then my rows being: 8am, 11am, and 2pm. I then conducted an Anova: Two-Factor Without Replication test on the data. Would both the rows and column data be important in this study or just the columns?
Thank you in advance.
Sri,
I have a few questions for you to help address your question:
1. Are all the air pollution measurements taken at the same place?
2. Do you care about differences in air pollution levels at different times of the day?
3. Do you care about differences in air pollution levels after one, two, three and four weeks after the plants were introduced?
Charles
Dear Charles,
First of all, thank you very much for your precious website and excel tools!
I am performing a repeated measures analysis in which I want to test the efficacy of a clinical treatment on a group of patients. So all the subjects are measured two times, before and after receiving the treatment.
As I read in your tutorial, sphericity is not an issue when only two groups of measures are involved.
Anyway, I verified that the variance of measurements perfomed on the sample in the pre-treatment condition is much higher than the variance of measurements in the post-treatment conditions. In effect, if I would check homogeneity of variances between the two groups with Levene’s test (I know this is not correct in this case, it’s just to make an example), the result would be a strong heteroscedasciticity.
My question is: how should I consider this large difference in variances? Does it affects in some way the results of my repeated measures test?
Thank you very much for your help!
Best Regards
Piero
Piero,
Levene’s test is valid also in the case where there are only two groups of measurements, but generally with two paired groups (before vs. after), you are interested in the paired differences, and so there is only one variance (of the differences) and not two.
With only two pairs, you can use the paired t test and don’t even need to bother with a repeated measures ANOVA.
Charles
Hi Charles,
Thanks so much for all the advice. Can you tell me how you arrived at the alpha value for the contrasts tests (it appears just above the p-value label in the contrasts tests table). I modified your contrast table to generate output for multiple planned contrasts, but I’m not confident I made the right choice when I compared all of the contrasts to that alpha value. Is it already adjusted for the number of measures? Do you recommend I change the weight to reflect the number of planned contrasts? I currently have 3 within subjects levels, and I’m running the following contrasts
1 -1 0
-1 0 1
0 1 -1
Thanks in advance for your help!
Anna,
In general, you should divide the alpha value (say .05) by the number of contrasts that you run (this is the Bonferroni correction). In the data analysis tool, this defaults to the number of groups plus one. Thus, with 3 groups, the value list for alpha should be .05/4 = .0125. Actually there is a programming error and I should actually be using the number of groups minus one. The reason for this is that I want to use as the default the number of orthogonal contrasts.
In any case, you can override the default value of alpha to whatever value you desire. If you have 3 contrasts you should use alpha = .05/3 = .01666.
Thanks for having me look at this so that I could find the error in the default value. I will change this in the next software release.
Charles
There is a little mistake in the Cohen d calculation. You switched the digits. It should say 1.71
Thomas,
Thanks for finding this error. I have now changed the website with the correct value. I appreciate your help in improving the website.
Charles
Spelling error just before the equation in Example 2 under the second “Observation” above…Turkey should be Tukey! Darn spell checker!
Gary,
Thanks for catching this. Turkey is clearly not the same as Tukey. I just corrected the webpage. Thanks for catching this error.
Charles
The following data represent the typical results from a delayed discounting study. The participants are asked how much they would take today instead of waiting for a specific delay period to receive $1000. Each participant responds to all 5 of the delay periods. Use a repeated-measures ANOVA with α = .01 to determine whether there are significant differences among the 5 delay periods for the following data:
participant 1 month 6months 1 year 2 years 5 years
A 950 850 800 700 550
B 800 800 750 700 600
C 850 750 650 600 500
D 750 700 700 650 550
E 950 900 850 800 650
F 900 900 850 750 650
HOW TO DO THIS EXCEL?
Surabhi,
Your problem is very similar to Example 1 of the referenced webpage, and so you can follow the approach shown for that example. Since you need to take sphericity into account, for completeness, see also Example 2 of the Sphericity webpage. To make things similar, you can use the Real Statistics One Factor Repeated Measures Anova data analysis tool, as described on the Sphericity webpage.
Charles
Hello,
We measured blood pressure to some subjects at 3 time points (before they took a drug, during effect and later on). I carried out a 1-way repeated-measures Anova (using the two factors without replication tool, as suggested), tested sphericity (GG epsilon = 0.77, HF epsilon = 0.99). Which post hoc test should I carry out? Just paired t-tests reducing my alpha with bonferroni or sidak corrections?
Thank you in advance.
Hello Stefano,
Which tests to use depends as always on what you are trying to prove. If you are only interested in comparing “before” with “after” you can simply perform a t-test with paired samples. If you want to compare all three combinations you can either use a Bonferroni or Sidak correction or perform Tukey HSD test. If you are interested in more complicated comparisons you may choose to use Contrasts. These options are described in Example 2 of the referenced webpage and the observations which follow the example.
Charles