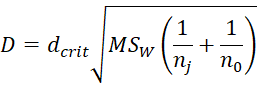Basic Concepts
Dunnett’s Test has the advantage that since fewer comparisons are made, there is less need to reduce the significance level to take experiment-wise error into account. Hsu’s Multiple Comparisons with the Best (MCB) also limits the number of comparisons made, this time instead of only considering comparisons with the Control, all comparisons are made to the group with either the highest mean or lowest mean (“the best”). Note that the highest or lowest sample group mean isn’t necessarily the highest or lowest population group mean.
Whether to use the highest mean or lowest mean needs to be decided in advance, before the analyses are started and ideally before any data is collected.
We first define
where dcrit is the critical value in the one-tailed Dunnett’s table at the given values of α, k (# of groups), and df (i.e. dfE).
For each group i, we define an interval [Li, Ui] as follows in the case where best means highest mean.
If, instead, best means lowest mean, then we use
We can also define a center value Ci where
Alternatively, we can define Ci by
Here, the first equation is used when best = highest mean and the second equation is used when best = lowest mean.
Note that when the group sizes are different, we can define the D-statistic as follows.
Since the values of dcrit are based on equal group sizes, the above formula is only accurate if the group sizes are not too different.
Worksheet Function
Real Statistics Function: The following function is provided in the Real Statistics Resource Pack:
DCRIT1(k, df, alpha, interp) = the critical value dcrit for k groups, the given degrees of freedom df, and the value of alpha. If interp = TRUE (default) the recommended interpolation is used; otherwise, linear interpolation is used.
Example
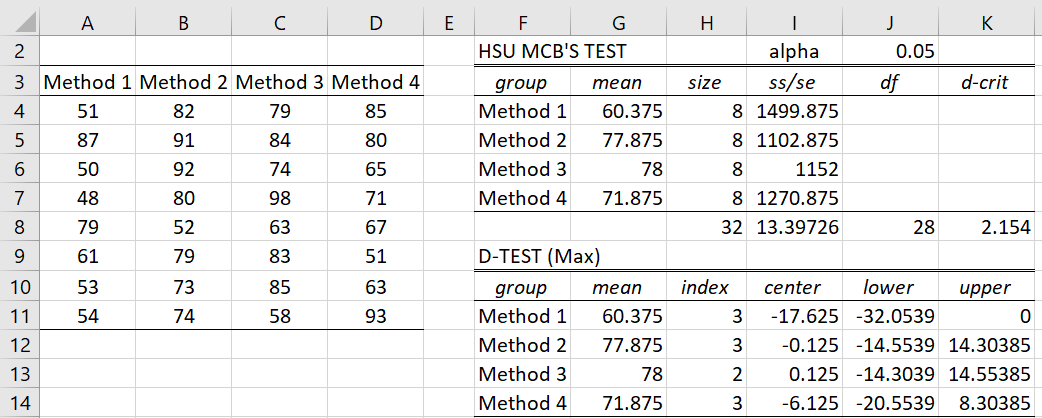
Example 1: Use Hsu’s MCB to determine, based on the data in Example 2 of ANOVA Basic Concepts, which groups are the best and which are significantly worse than the best. Here “best” means has the highest mean value.
We see from the analysis shown in Figure 1, that Method 1 is significantly worse than the best (since upper = 0) and there is no significant difference between the other methods and the best method (since zero is contained in these confidence intervals).
Figure 1 – Hsu’s MCB
| Cell | Value | Formula |
| G4 | Mean for Method 1 | =AVERAGE(A4:A11) |
| H4 | Method 1 group size | =COUNT(A4:A11) |
| I4 | SS for Method 1 group | =DEVSQ(A4:A11) |
| H8 | Sample size | =SUM(H4:H7) |
| I8 | Standard error | =SQRT(SUM(I4:I7)/J8) |
| J8 | dfE | =H8-COUNTA(F4:F7) |
| K8 | dcrit | =DCRIT1(COUNT(H4:H7),J8,J2) |
| H11 | k≠1: x̄k > x̄j for all j≠1 | =INDEX_MAX(G$11:G$14,G11) |
| I11 | C1 | =G11-INDEX(G$11:G$14,H11) |
| J11 | L1 | =MIN(0,G11-INDEX(G$11:G$14,H11)-I$8*K$8*SQRT(1/H4+1/INDEX(H$4:H$7,H11))) |
| K11 | U1 | =MAX(0,G11-INDEX(G$11:G$14,H11)+ I$8*K$8*SQRT(1/H4+1/INDEX(H$4:H$7,H11))) |
Figure 2 – Formulas from Figure 1
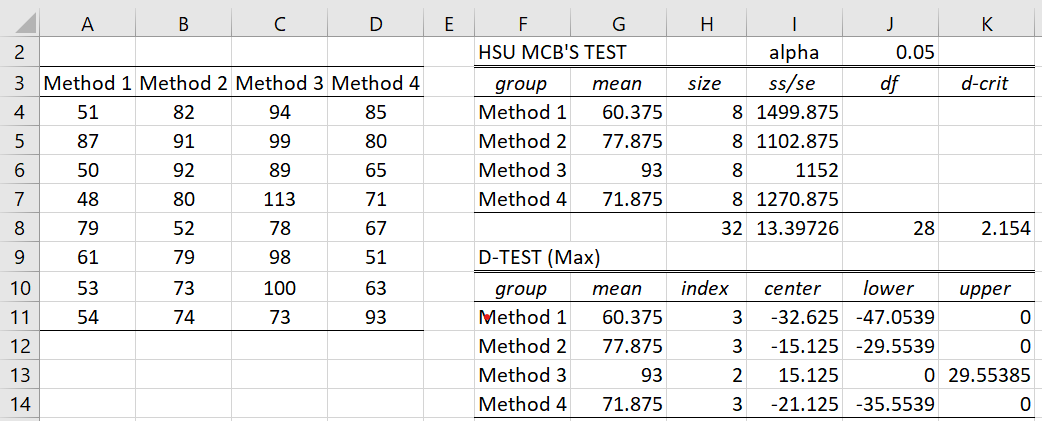
Observation: If all the values in Method 3 are increased by 15, we would get the results shown in Figure 3. In this case, Method 3 is significantly better than the other methods (since Method 3 is the only one with a positive upper-bound).
Figure 3 – Revised Hsu’s MCB
The analysis is similar when “best” means “the smallest mean”. Figure 4 summarizes how to interpret the results.
| Highest is best | Smallest is best | |
| lower < 0 < upper | no difference from best | no difference from best |
| lower = 0, upper > 0 | better than other groups | worse than best |
| lower < 0, upper = 0 | worse than best | better than other groups |
Figure 4 – Interpretation of Hsu’s MCB
Data Analysis Tool
Real Statistics Data Analysis Tool: We use the Single Factor ANOVA tool to perform Hsu’s MCB post-hoc test. When the dialog box shown in Figure 1 of One-Factor ANOVA Analysis Tool appears, fill in the Input Range with A3:D11, make sure that the Column headings included with data is checked and choose the Hsu MCB (Max) option. After clicking on the OK button, the output shown on the right side of Figure 1 is displayed.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Hsu, J. C. (1996) Multiple comparisons, theory and methods. Chapman & Hall/CRC
https://books.google.it/books?id=8AK8PUbw3lsC&pg=PA81&source=gbs_toc_r&cad=4#v=onepage&q&f=false
Minitab (2019) What is Hsu’s multiple comparisons with the best (MCB)?
https://support.minitab.com/en-us/minitab-express/1/help-and-how-to/modeling-statistics/anova/supporting-topics/multiple-comparisons/what-is-hsu-s-mcb/