Basic Concepts
A better alternative to Tukey-Kramer, when group variances are unequal, is the Games-Howell test. Here the standard error becomes
Thus we use different pooled variances for each pair instead of the same pooled variance MSW. We employ the following test
where the standard error is as above and q′crit is the critical value of the Studentized range statistic but with the degrees of freedom given by df′ as defined in Two Sample t-Test with Unequal Variances, namely
In this way, we also take care of the case where the variances are unequal in exactly the same manner as in Property 1 of Two Sample t-Test with Unequal Variances, except that we now use the q-statistic instead of the t-statistic. Note that the supplemental function DF_POOLED can be used to calculate df′.
Example
Example 1: Repeat Example 1 of Tukey-Kramer Test using the Games-Howell test.
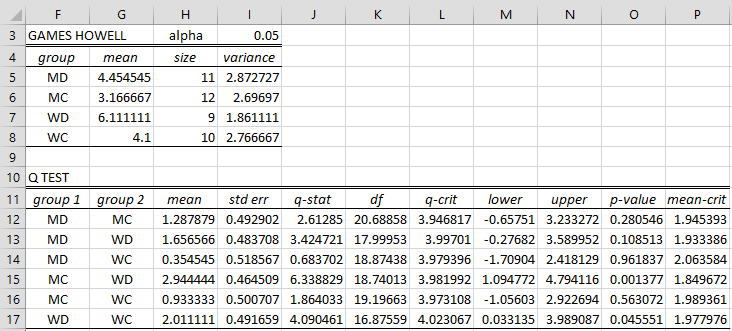
We repeat the same steps as we used in Example 1 of Tukey-Kramer except that we choose the Games-Howell option. The output of the test is shown in Figure 1.
Figure 1 – Games-Howell Data Analysis
Note that the group variances are fairly similar, and so we shouldn’t expect much of a difference between the results from the Games-Howell and Tukey-Kramer tests.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Howell, D. C. (2010) Statistical methods for psychology (7th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf
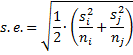
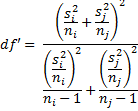
Hi Charles, I have a data set of 6 treatments, each run in biological triplicate and 2 conditions, for a total of 36 independent unpaired samples and equal sample size. The normality assumption was met, but I have to deal with heterogeneous variances, with no chance of finding a good data transformation. So, I performed anyway Two-Way ANOVA (any suggestion on how much variance deviation in the different groups is acceptable to consider them as similar and not diverse?), followed by the Games-Howell post-hoc test. Some results gave a negative p-value. I doubt that a a negative p-value is possible.. Maybe I misapproach?
Hi Niurka,
What do you mean by biological triplicate?
ANOVA may be able to tolerate differences in variances as much as the variance of one group 4 times another.
You shouldn’t get a negative p-value. If you get a value such as -1.7E-07 then despite the number being negative you should view it as zero.
Charles
Hi Charles, thank you for your reply. With biological triplicate, I mean that I have 3 independent replicates for each treatment. In this way, I have 6 treatments, each one with 3 replicates, performed in 2 different conditions (2 time points, with unpaired data). After unsuccessful data transformations for the need for homogeneous variances, I performed the Two-Way ANOVA followed by the Games-Howell post-hoc test and I got some negative p-values, such as the following: -0.0000125242.
So, I’m confused about how to represent it in a table chart with the significance level.
Hi Niurka,
I can’t say for sure without seeing your data and test results, but negative results near zero can be caused by round off error. In this case, I would just treat -0.0000125242 as zero. Usually, though the negative result is a bit closer to zero: e.g. -1.3E-8.
Charles