Outliers in ANOVA

Testing for outliers

We have the following ways of identifying the presence of outliers:

  • Side by side plotting of the raw data (histograms and box plots)
  • Examination of residuals

Residuals are defined as for Levene’s test, namely:

Residuals Levene's test

The residual is a measure of how far away an observation is from its group mean value (our best guess of the value). If an observation has a large residual, we consider it a potential outlier. To determine how large a residual must be to be classified as an outlier we use the fact that if the population is normally distributed, then the residuals are also normally distributed with distribution

eij ∼ N(0, MSW)

Thus approximately 4.56% of the observations should be more than 2 standard deviations away from its group mean, 1.24% should be more than 2.5 standard deviations away, 0.26% should be more than 3 standard deviations away, etc. Any deviations from these norms can be viewed as indicating the presence of potential outliers.

Example

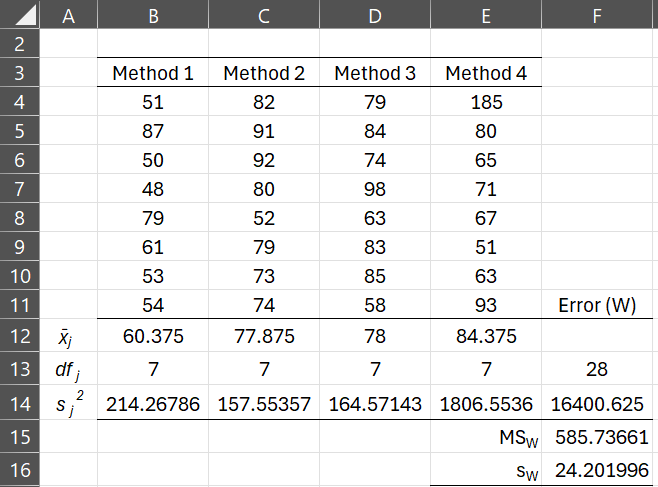
Example 1: Determine whether there are any outliers for the data in Example 2 of Basic Concepts for ANOVA if we change the first sample for Method 4 to 185 (instead of 85).

MSW calculation one-way ANOVA

Figure 1 – Identifying outliers (part 1)

In Figure 1, we calculate MSW as we did in Example 3 of Basic Concepts for ANOVA. From this we calculate the standard error sW = SQRT(MSW) = 24.2.

Since residuals are presumed to be normally distributed with mean 0 and standard deviation sW, we can standardize the residuals to obtain the results in range B21:E28. For example, cell B21 contains the formula =(B4-B$12)/$F$16.

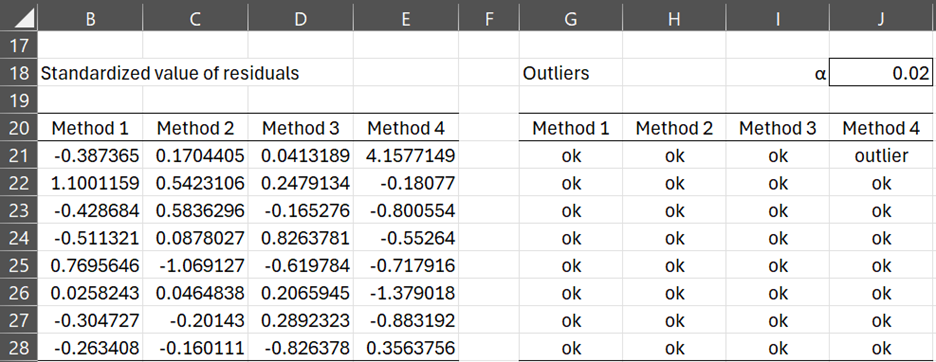
Residuals and outliers

Figure 2 – Identifying outliers (part 2)

We define an outlier based on an alpha value. Here we choose α = .02, and so we label any of the original data items as an outlier if its standardized residual has normal value in the critical range defined by alpha.

E.g. we see that the first sample element for Method 4 is labeled an outlier (in cell J21) since NORM.S.DIST(ABS(E21),TRUE) = NORM.S.DIST(4.16, TRUE) > .99 = 1 – α/2.

Dealing with outliers

Once a potential outlier has been identified, first check the data to make sure the outlier is not a data entry or data coding error. If not you can conduct a sensitivity analysis as follows to see how much the outlying observations affect your results.

  • Run ANOVA on the entire data.
  • Remove outlier(s) and rerun the ANOVA.
  • If the results are the same then you can report the analysis on the full data and report that the outliers did not influence the results.
  • If the results are different, try running a non-parametric test (e.g. Kruskal-Wallis) or simply report your analysis with and without the outlier.

Two other approaches for dealing with outliers are to use trimmed means or Winsorized samples (as described in Outliers and Robustness) or to use a transformation. In particular, a reciprocal transformation f(x) = 1/x can be useful.

For example, if in measuring response times for a rat in maze, suppose the following times were recorded:

20, 21, 24, 26, 30, 31, 33, 95, 230

It is quite possible that two of the rats simply got bored or got distracted and so the results are quite distorted. In this case, the use of a reciprocal transformation tends to reduce the effect of long times. Effectively you are transforming time into speed. The transformed data are:

.0500, .0476, .0417, .0385, .0333, .0323, .0303, .0105, .0043

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Halldestam, M. (2016) ANOVA – the effect of outliers
http://www.diva-portal.se/smash/get/diva2:935253/FULLTEXT01.pdf

Howell, D. C. (2010) Statistical methods for psychology (7th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf

15 thoughts on “Outliers in ANOVA”

  1. I should be grateful if someone could provide an explanation to the following situation:

    The outcome of a statistical analysis of a bioequivalence study ( 2 arms of generic product-population 38) is for me a difficult to understand

    one subject, in one arm of the study, showed a very limited absorption of the tested drug. the statistical analysis showed by including the data of that one individual/one arm, bioequivalence failed with very wide Confidence Interval

    By removing the data of that one individual, Confidence Interval value has narrowed significantly and test/reference products showed bioequivalnce

    Is that possible? data from 1/38, one leg, alters dramatically the value of CI?

    I should be grateful for any assistance

    Yours

    Riad Ayech
    ayechc@aol.com

    Reply

    • Hello Riad,
      Theoretically, this is possible. Outliers can distort the analysis. Whether this is true in the case that you are referring to, I can’t comment on since I am unfamiliar with the details.
      Charles

      Reply

      • Thanks Charles;
        It is unusual situation whereas the results of one volunteer/ only one leg of the study out of 40 changed the value of CI from success to failure ,

        1- Extremely wide range of mean values for both Cmax and AUC.
        Test Reference
        Cmax

        Thanks Charles

        As you see from the summary of the results below, the measurements of one volunteer/one leg out of 40 volunteers have distorted the value of CI from success to failure. You will see how the range was wide for the two concerned parameters. Is there any statistical way to deal with this situation? Best Regards Riad

        Cmax ( range) : 0.658-129.3 11.9-105.7
        AUC (range): 1.29-1901.7 314.2-1807.2

        – As a result, an extremely wide values of the calculated ratio (Test/reference) were calculated
        • Cmax: 3.43-145.8
        • AUC: 0.36-147.0
        Thanks Charles

        Reply

        • Riad,
          Assuming all the calculations are correct, you shouldn’t try to change the results of the analysis. They are what they are.
          If one specific observation is a suspected outlier, you might want to understand the nature of this observation. Do you suspect that it is truly an unusual event and so is distorting the analysis? (e.g. perhaps the measurement was done poorly or there was something non-random about the observation). If so, then you might consider reporting the results with and without this observation.
          Charles

          Reply

  3. Hi Charles
    First my objective is :
    * take data without outlier and analyze the data
    * put outlier in the data (one on each operator and one on all)
    *analyze the data with outlier
    *identify outlier in the data and handle the outlier
    * find a best method that is identify and handle the outliers
    * my data contains 30 measurements (3 operators 5 parts 2 replications)
    My question is :is there any method can identify and handle outlier in Nested ANOVA
    The webpage you mentioned above is not appeared
    Thanks

    Reply

    • Hi
      I have a Nested design it is for Gage R&R
      How can I detect outliers in this Nested design which is based on ANOVA .Is it the same way that you mentioned above or there are different way and what software could help me to detect outliers in Nested Gage R&R and which ways can deal with this outliers?

      Reply

Leave a Comment