Nominal-Ordinal Chi-square Test

In Independence Testing, we describe how to perform testing for contingency tables where both factors are nominal. In Ordered Chi-square Testing for Independence, we describe how to perform similar testing when both factors are ordinal. On this webpage, we consider the case where one factor is nominal and the other is ordinal.

Example

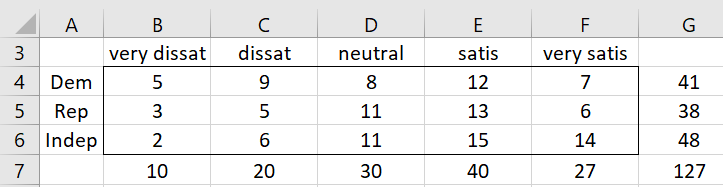
Example 1: 127 people who attended a training course were asked to rate their satisfaction with the economy as very dissatisfied, dissatisfied, neutral, satisfied and very satisfied. We would like to know whether their level of satisfaction is independent of their political party category (Democrat, Republican, Independent) based on the contingency table shown in Figure 1.

Figure 1 – Nominal-ordinal contingency table

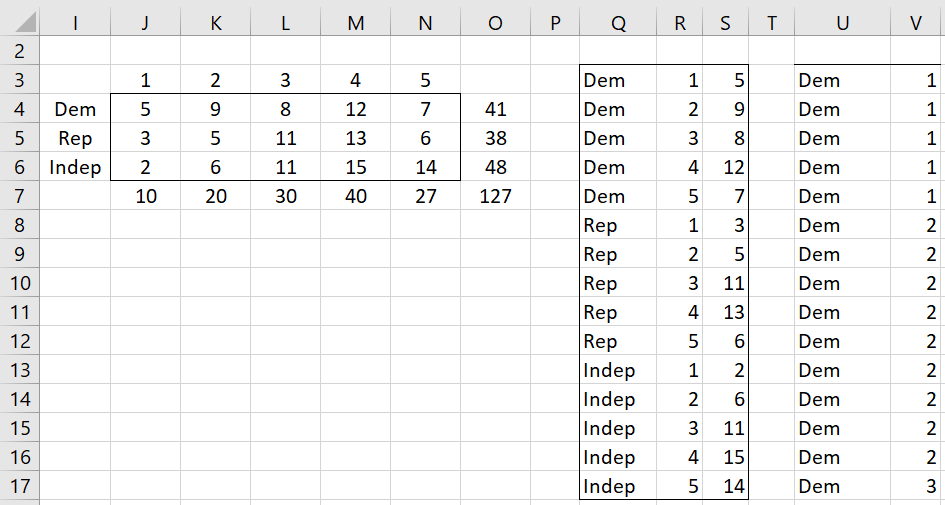
Here, the row factor is nominal and the column factor is ordinal. If we also assume that the column factor has a Likert scale, then the contingency table can be represented as shown on the left side of Figure 2.

Figure 2 – Reformatting for Kruskal-Wallis

We can use Kruskal-Wallis to test whether the median satisfaction values of the three political parties are significantly different. To do this, we must first reorganize the data.

We first insert the array formula =Anova2Std(I3:N6) in range Q3:S17 and then the array formula =FREQ2RAW(Q3:S17) in range U3:V114 (only the first 15 of 127 rows are displayed). This latter range represents the data in standard format required for the Kruskal-Wallis test. Using the One-Factor ANOVA data analysis tool, we obtain the results of the Kruskal-Wallis test as shown in Figure 3.

Figure 3 – Kruskal-Wallis Test

Columns X, Y and Z show the data in U and V reformatted Excel format for ANOVA. We see that p-value = .145, and so there is no statistical difference between the parties regarding their satisfaction with the economy. If a significant result had been detected, then follow-up testing could be done using the One-Factor ANOVA data analysis tool.

Real Statistics Support

Click here for Real Statistics Support for Nominal-Ordinal Independence Test.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Howell, D. C. (2001) Chi-square with ordinal data
https://www.uvm.edu/~statdhtx/StatPages/More_Stuff/OrdinalChisq/OrdinalChiSq.html

Agresti, A. (1996) An introduction to categorical data analysis. New York: Wiley.

Agresti, A. (1981) Measures of nominal-ordinal association
https://users.stat.ufl.edu/~aa/articles/agresti_1981.pdf

Beh, E. J. (2008) Simple correspondence analysis of nominal-ordinal contingency tables
https://www.researchgate.net/publication/26501604_Simple_Correspondence_Analysis_of_Nominal-Ordinal_Contingency_Tables

Starkweather, J. (2020) Nominal and ordinal variable analysis
http://bayes.acs.unt.edu:8083/BayesContent/class/Jon/ISSS_SC/Module011/isss_m11_nomord/