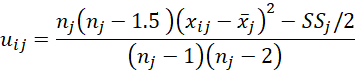O’Brien’s Test

Basic Concepts

As in Levene’s test, for O’Brien’s test of the homogeneity of group variances, we perform ANOVA on a transformation of the group data. For this test, we use the following transformed data uij where xij is the score of the ith element in the jth group,

Transformed data

SSj is the sum of the squared deviations from the jth group mean, and

Sum squared group deviations

nj is the number of elements in the jth group.

Example

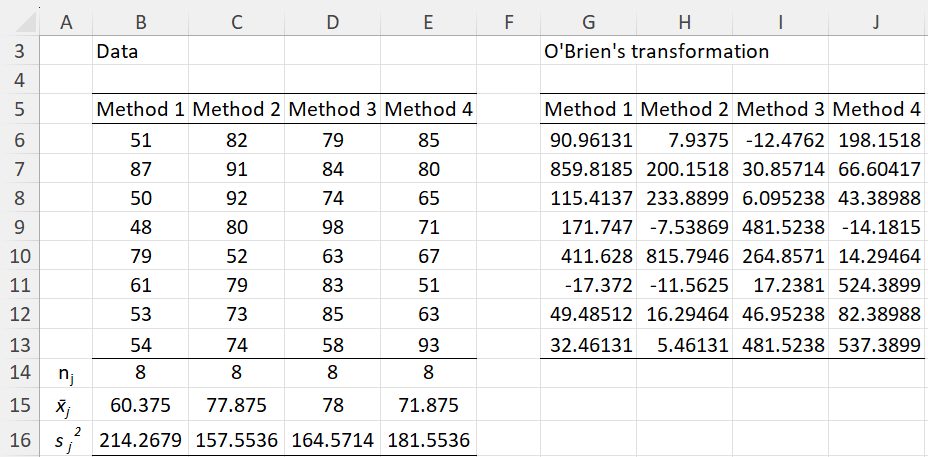
Example 1: Repeat Example 1 of Levene’s Test (the data is repeated on the left side of Figure 1).

The transformation of the data is shown on the right side of Figure 1.

Transformation of the data

Figure 1 – O’Brien’s transformation

For example, cell G6 contains the formula

=IF(ISNUMBER(B6),B$14*(B$14-1.5)*(B6-B$15)^2/((B$14-1)*(B$14-2))-B$16/(2*(B$14-2)),””)

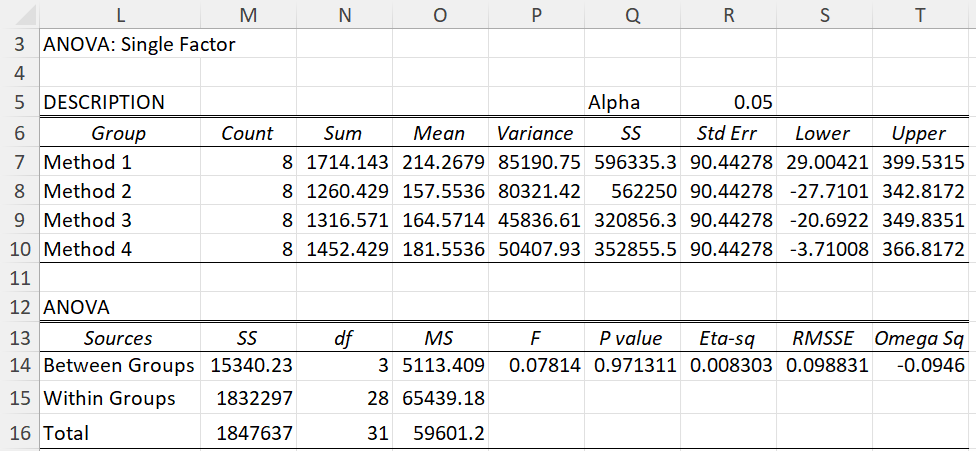
We can now perform ANOVA on the transformed data using the Real Statistics One Factor Anova data analysis tool (see Confidence Interval for ANOVA) as shown in Figure 2.

O'Brien's test example

Figure 2 – O’Brien’s test

Since p-value = .971311 (cell Q14), we can’t reject the null hypothesis that the group variances are equal. In fact, we conclude that the homogeneity of variances assumption is quite likely to hold.

Worksheet Function

Real Statistics Function: The Real Statistics Resource Pack provides the following worksheet function:

OBrienTest(R1) = p-value of O’Brien’s test for the data in R1

This function ignores blank entries in R1.

For Example 1, the output from the formula =OBrienTest(B6:E13) is .971311.

Ramsey’s Conditional Test

Ramsey noted that when the group kurtosis < 0 then O’Brien’s test tends to be best, while if the group kurtosis ≥ 0 then the Brown-Forsythe test (i.e. Levene’s test using deviations from the median) tends to be best.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Abdi, H. (2007) O’Brien test for homogeneity of variance
https://www.utdallas.edu/~herve/Abdi-OBrien2007-pretty.pdf

Ramsey, P. H. (1994) Testing variances in psychological and educational research
https://psycnet.apa.org/record/1994-28101-001

Wang, Y. et al. (2016) Comparing the performance of approaches for testing the homogeneity of variance assumption in one-factor ANOVA models
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5965542/#bibr32-0013164416645162