Basic Concepts
For Levene’s test of the homogeneity of group variances, the residuals eij of the group means from the cell means are calculated as follows:
An ANOVA is then conducted on the absolute value of the residuals. If the group variances are equal, then the average size of the residual should be the same across all groups.
Example
Example 1: Use Levene’s test to determine whether the 4 samples in Example 2 of Basic Concepts for ANOVA have significantly different population variances.
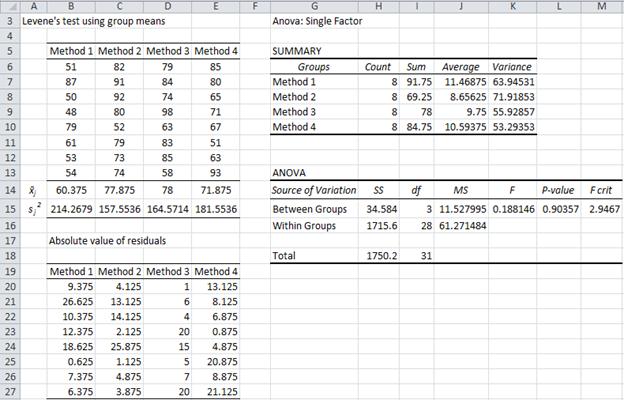
Figure 1 – Levene’s test for Example 1
Since p-value = .90357 > .05 = α (Figure 1), we cannot reject the null hypothesis and conclude there is no significant difference between the 4 group means. Consequently, the ANOVA test conducted previously for Example 2 of Basic Concepts for ANOVA satisfies the homogeneity of variances assumption.
Versions of the test
There are three versions of Levene’s test:
- Use the mean (as in the explanation above)
- Use the median (replace mean by median above)
- 10% trimmed mean (replace mean by 10% trimmed mean above)
The three choices determine the robustness and power of Levene’s test. By robustness, we mean the ability of the test to not falsely detect unequal variances when the underlying data are not normally distributed and the variables are in fact equal. By power, we mean the ability of the test to detect unequal variances when the variances are in fact unequal.
Levene’s original paper only proposed using the mean. Brown and Forsythe extended Levene’s test to use either the median or the trimmed mean. They performed Monte Carlo studies that indicated that using the trimmed mean performed best when the underlying data had a heavy-tailed distribution and the median performed best when the underlying data had a skewed distribution. Using the mean provided the best power for symmetric, moderate-tailed, distributions.
Although the optimal choice depends on the underlying distribution, the definition based on the median is recommended as the choice that provides good robustness against many types of non-normal data while retaining good power. Another choice may be better based on knowledge of the underlying distribution of the data.
Caution
You need to assume that the absolute values of the residuals satisfy the assumptions of ANOVA. Also, a more liberal cut-off value when testing homogeneity of variances is often used due to the poor power of these tests.
Worksheet Function
Real Statistics Function: The following supplemental functions contained in the Real Statistics Resource Pack compute the p-value for Levene’s test.
LEVENE(R1, type) = p-value for Levene’s test for the data in range R1. If type = 0 then group means are used; if type > 0 then group medians are used; when type < 0 then 10% trimmed group means are used. If the second argument is omitted it defaults to 0.
This function ignores any empty or non-numeric cells.
For example, for the data in Example 1, LEVENE(B6:E13) = LEVENE(B6:E13, 0) = 0.90357 (referring to Figure 1). Note that, for the same data, LEVENE(B6:E13, 1) = 0.97971 and LEVENE(B6:E13, -1) = 0.90357.
Data Analysis Tool
Real Statistics Data Analysis Tool: A Levene’s Test option is included in the Single Factor Anova data analysis tool. This option displays the results of all three versions of Levene’s test.
To use this tool for Example 1, enter Ctrl-m and select Single Factor Anova from the Anova tab (or from the main menu when using the original user interface). A dialog box similar to that shown in Figure 1 of Confidence Interval for ANOVA appears. Enter B5:E13 in the Input Range, check Column headings included with data, select the Levene’s Test option and click on the OK button.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Wikipedia (2015) Levene’s test
https://en.wikipedia.org/wiki/Levene%27s_test
Field, A. (2009) Discovering statistics using SPSS. 3rd Ed. SAGE.
Aloha. I appreciate your teachings.
It seems that under Levene’s Test, classic ANOVA is applied to the absolute value of residuals. Isn’t it possible (or more precise) to apply Welch’s ANOVA to the absolute value of residuals?
Good day.
Aloha Seth,
It is certainly possible to do this and it seems to make sense, but I don’t know how good this test would be for determining the homogeneity of variances (presumably when there isn’t normality).
Charles
Thanks.
That sounds reasonable.
You are super.
Many thanks for this website and free resources, I am finding them very helpful.
However, I’m having trouble with the Levene’s test. The “median” result seems fine, but the generated p values for “means” and “trimmed means” are peculiar: “7.13765E-10”, “6.99842E-10” “3.39378E-07”, “3.17442E-07”.
I know I must be doing something wrong. Do you have any idea what that might be?
Thank you!
Hi Rachel,
These are reasonable values, which you should interpret as very close to zero. The values are written in scientific notation. E.g. 3.39378E-07 is equivalent to .000000339378.
Charles
When using the Single factor ANOVA in from the Real Stats package, why does the test always exclude to first point of the selected arrays?
Hello Jorge,
This depends on whether or not you choose the Column headings are included with data option is selected. If you use column headings then you don’t want these to be considered to be data and so the first row is excluded; otherwise you don’t want the first row to be excluded.
Charles
Hi Charles, in the paper https://sciendo.com/article/10.1515/cttr-2017-0014, the author proposed to use a L0 Levene’s Test instead of Cochrane to analyze standard deviation outliers in ISO 5725-2. In the case of odd number of replicates, the central data represent the median, so the difference between median and central data = 0. In the paper this difference was omitted from ANOVA test. I followed your indications and the results (p) of ANOVA is equal to LEVENE test (using Median in Real Statistic), but only if the central data (=0) of all samples are considered (not excluded). If I exclude the central differences (=0) results are different.
I would like to know your opinion about the different approach.
Many thanks
Hello Dino,
Sorry, but I am not familiar with this approach.
Charles
Hi, thanks for all your posts I really appreciate it. I do however have a question. I’m trying to perform a 2 way ANOVA, and the data has unequal variance… that is, I’m getting a p value of <0.05 on the Levene's test. What options do I have to analyse the data? I understand that doing a 1 way ANOVA with Welch and Games Howell tests is an option, but as I mentioned I'm trying to assess the potential interaction between two independent variables and the way they influence the Dependent variable? Thanks in advance for any advice.
Hi Sam,
You can use a non-parametric test instead of two-way ANOVA. Two approaches are described on the Real Statistics website:
https://www.real-statistics.com/two-way-anova/scheirer-ray-hare-test/
https://www.real-statistics.com/two-way-anova/aligned-rank-transform-art-anova/
In addition, you can use resampling. The approach for one-way ANOVA is described at:
https://www.real-statistics.com/one-way-analysis-of-variance-anova/resampling-anova/
The two-way version of resampling is similar, although I have not yet implemented it in the Real Statistics software.
Charles
Thanks so much for your quick response really appreciate it
Dear Chales,
I needed to analyse 4 independent columns of data (1 control group, 3 treatment groups) in order to:
1. see if there is a significant difference between the control group and each of the 3 groups?
2. compare the 3 treated groups with each other to see which of the 3 groups has more different data in comparison with the control group?
(all data are numeric and there are 16 numbers for each group resulted from 16 times repeating the test)
Which statistical tests would you recommend?
Best regards,
Nafis
Hello,
Assuming that you have 16 samples elements for each group, then
1. This seems like a fit for one-way ANOVA (assuming the assumptions for the test are met) with Dunnett’s post-hoc test.
2. I don’t understand what you mean by “has more different data”. If you want to compare each of the treatments with the control, then Dunnett’s test is a reasonable approach. If you want to compare the three treatments with each other, then a post-hoc test like Tukey’s HSD may be best. In this case, you probably don’t want to use Dunnett’s test as well.
Charles
In my study, i am using independent samples t test (to compare gain scores of experimental and control group). Do i need to apply levene’s test before using t test.
You can use Levene’s test to see whether the sample variances are significantly different. Generally, you can avoid this by just looking at the variances. If they are fairly similar you can use the t test with equal variances; otherwise, you can use the t test with unequal variances.
Charles
Hello,
I have a simple inquiry, please…
my data is not normally distributed and in the Levene test showed my data is homogenous (no significant difference when I use center=median), although the visual inspection revealed not symmetrical distribution.
I have tried with transformation methods won’t help.
I am confused about which version of the Levene’s test I should follow:
if I do the mean or trimmed mean = it gave me not homogenous data but with the median = homogenous? (I have zeros in my data)
however, I am trying to make a Kruskal test to compare the differences in the number of the isolated pathogen between 3 groups (total of 60 samples).
I appreciated your suggestion.
thank you,
Mohammed.
Hello Mohammed,
I believe that the median version of Levene’s test is the one that is most commonly used. If the other versions of Levene’s test are not too significant then you are probably ok proceeding with Kruskal’s test.
Charles
Hi, I am running a 2-way ANOVA test.
However, the levene’s test is significant – variances are not equal.
What should i do in order to continue ?
Hello Krixie,
The usual approach is to use Welch’s ANOVA, but see the advice on
https://real-statistics.com/one-way-analysis-of-variance-anova/homogeneity-variances/dealing-with-heterogeneous-variances/
Charles
Hi Charles,
When using the Levenes real stats function on some of my own data a got just plain 0 for the p value. Does that mean that there was an error or is there just a lot of difference in regards to the variances of my samples.
Thanks for everything,
Ian Moffit
Hello Ian,
It is certainly possible for p-value to be equal to zero, in which case the homogeneity of variance assumption would not be met.
Charles
Hi,
I have problems to perform ANOVA. My data is mostly normally distributed but when I do Levene’s test, I will get very different results whether it is based on mean (usually shown unequal) or median (usually shows equal). Also the subsequent results of Tukey’s and Games-Howell tests are very different. Which result to follow in Levene’s test: based on mean or median?
Kathy,
It is not so strange to get get different results from different versions of the Levene’s test. You need to use your judgement as to what to do in this case, although generally the median version of the test is the one that is used. Remember that Levene’s test is not to test for normality. With unequal variances, Games Howell is preferred over Tukey’s HSD.
Charles
Dr Zaiontz,
Thank you for providing the realstats package! Your site is a very helpful teaching tool for the non-quantitative mind. I have run a single factor ANOVA, Levene’s, and a Tukey-Kramer test to compare habitat quality across several sites with unequal numbers of samples.
My question is about interpreting the Levene’s test: my p-value for all 3 types is .03, does this mean that the variance of my data is unequal and thus not fit to use the ANOVA and Tukey’s test?
Thank you,
Alissa
Alissa,
Yes, since p = .03 < .05 = alpha. If the sample sizes were equal, I would probably use ANOVA, but since the sample sizes are unequal I would be more cautious and probably elect to use Welch's ANOVA and Games-Howell. Charles
Charles, thank you for your response. I have tried the Games-Howell instead of Tukey’s as you suggested and have two further questions. With Games-Howell how to I decipher which groups are found to be similar or not? Is that somehow expressed in column “c”? Also, I am experiencing some errors that I have been unable to resolve. Below are my Games-Howell results, do you have any insight as to what I have done wrong?
GAMES HOWELL Alpha 0.05
Groups c mean n variance c^2*var/n
A 0.68 43 0.01 0
B 0.83 32 0.00 0
C 0.50 53 0.04 0
D 0.79 34 0.01 0
E 0.83 34 0.00 0
F 0.89 34 0.00 0
G 0.82 35 0.01 0
0 0 265 0
Q TEST
std err q-stat df q-crit lower upper p-value x-crit
0 the rest (q-stat to x-crit) all come out as errors
Oh dang, the results got re-formatted once the comment was posted. Ok I’ll have to explain more. Column “c” was empty except for the very bottom row = 0. The bottom row of variance was blank. The rest of the rows are in order just squished.
Q Test. Only std err had a result = 0. q-stat and df were “divide by 0 error” and the rest were “error in value.”
Hope this makes sense, sorry for the confusion.
Alissa,
See my previous response. I don-t know why the rows are squished. If this problem remains, you can send me an Excel file with your data and test results and I will try to figure out what is happening.
Charles
Alissa,
To compare two groups you need to place +1 in the c column corresponding to that group and -1 in the c column corresponding to the other group. All the errors should then go away. You can make multiple pairwise comparisons by changing which cells contain the +1 and -1.
Charles
Charles,
I see! I did not understand before that I had to manually add the 1/-1 to make this work. Thank you so much for your time.
Alissa
Hi Charles
Hope you are well.
I am running a t test between a sample group and norm group (want to see if the norm group we are using for an ability test is appropriate for our sample of supervisors). In order to run the levene test, the real stats function requires having the data for the norm group also. What if I only have the mean and sd and cohen’s d? How would I check for homogeneity of variance? Thanks.
Demos
Demos,
Instead of using Levene’s test, you should consider the one-sample variance test using the chi-square distribution, as described at
https://real-statistics.com/chi-square-and-f-distributions/one-sample-hypothesis-testing-variance/
Charles
Hi, if I have to compare means about tu groups n1=n2=15, do I have to use levene first to check if variances are equal?
Thanks
Nayiv Assaf
Nayiv,
Whether you use Levene’s test or not depends on whether homogeneity of variance is a requirement for some other statistical test. E.g. with only two samples, you generally wouldn’t use Levene’s test before using a t test since you could use a correction factor even if homogeneity of variances is violated.
ok, yes, I understant. Thank you very much
Need email of any statistician. i have 4 0r 5 questions that i need to ask. Need help
Muhammad,
You can ask one of your questions here.
Charles
Hi Charles,
I am in my undergraduate thesis. I am going to test the relationship between age factor and brand awareness. I ran Levene Test and got the result below. However, i find that my first table “Test of Homogeneity of Variances” is different from yours, so i wonder if my result has any errors. And i also find out that the coefficient of Sig. is over 0.05 but the coefficient of Sig. in the second table is below 0.05. There are any problems with my Levene’s Test.
Thanks and regards,
Courtney
Test of Homogeneity of Variances
Levene Statistic df1 df2 Sig.
2,418 3 152 ,069
ANOVA
Sum of Squares df Mean Square F Sig.
Between Groups 6,158 3 2,053 38,659 ,000
Within Groups 8,071 152 ,053
Total 14,228 155
Courntey,
Remember that there are three versions of Levene’s test (mean, median, 95% trimmed mean). You need to make sure that you are using the same version.
Charles
Hi Charles,
So just to clarify, we can obtain the results for the LEVENE’s test by EITHER,
1) Use the Real Statistics Data Analysis Tool and select ‘Levene’s test’ etc.
OR
2) Calculate a regular ANOVA on the residuals of the 1) mean, 2) median and 3) Tmean and refer to the p-value in output of the data table
Or are we calculating the ANOVA on the residuals to satisfy another assumption of the LEVENE’s test…?
Many thanks,
Alli
Alli,
What other assumption are you referring to?
Charles
I suppose this was where my confusion was – if the two tests for LEVENE (using the Analysis tool, which brings up the same results as calculating an Anova on the residuals for each the mean, median and Tmean) were simply two ways of calculating Levene’s test, or if the ANOVA on the residuals (in your example) was a test for something else I wasn’t aware of (i.e. perhaps an assumption I wasn’t aware of). Hope that makes sense. Thanks so much for your help. I’m so thankful to have found this webpage . I find it much easier than writing the code for these analyses in R!
Hi,
I have carried out a 2 by 2 between ANOVA, and the levene’s test is significant, how do I transform the data?
Thanks,
Ellie.
Ellie,
I couldn’t tell you a priori what a suitable transformation could be.
Charles
hello Charles,
what does it mean if my Kruskal-Wallis significants and Levene Significant contradicts one another? KW = 0.154 LS = 0.000
is it possible for you to clarify this for me.
thank you
Chantal
You are comparing apples with oranges. Levene’s test tests whether the variances are equal, while Kruskal-Wallis tests whether means are equal. With a significant Levene’s test, generally you are better off using Welch’s ANOVA rather than Kruskal-Wallis.
Charles
Hello Charles,
I’m trying to compare 3 groups (different administration routes for medicines) which I need to know if there are differences in the means between them and in pairwise comparisons. The groups sizes are unequal (16, 5 and 10) and variances too (23,58; 4,30 and 5,16). Shapiro-Wilk tests for each group demonstrate normality (p-value > alpha) and Levene’s tests are significant too (p-value for means, medians and trimmed > alpha), so demonstrating homogeneity in variances. My question is: should I use ANOVA or Welch’s test to analyse it? After the first test (for the 3 groups) how analyse it in pairwise comparisons? Two sample t test for unequal variances or Games-Howell’s test?
Thank you so much!
Renan,
Given variances 23,58; 4,30 and 5,16, I am surprised that you didn’t get a significant result for Levene’s test. In any case, if the normality assumption is met but the homogeneity of variances assumption is not met (esp. with unequal sample sizes), then Welch’s test is probably best. Games-Howell is probably the right post-hoc test.
Charles
I have a data set containing concentration values from 2 substrate types and 4 different habitats, so far the Levene Test is showing that the variances are different. Is there a way to tell exactly where these differences are, like a post hoc test?
Kristen,
Since Levene’s test is actually a version of ANOVA, I guess so, but why would you want to do this?
Charles
Charles,
I am interested in determining where the variances between my different variables are statistically different from one another. So, I have a 2 by 4 factorial setup and need to know where the variances are statistically different between each combination, similar to like a post hoc test would for means.
Is this possible and how do I obtain these values?
Thank you,
Kristen
Kristen,
Levene’s test is a form of ANOVA as shown in the following webpage
https://real-statistics.com/one-way-analysis-of-variance-anova/homogeneity-variances/levenes-test/
If you need to follow-up perhaps you can use Tukey HSD or contrasts
Charles
Hi Charles,
I want to use the Levene Test as a verification of homo- or heterogeneity of the variance for the T-Test. Do I simply say if the p-value of the Levene is >alpha=0,05 the variance is heterogenic? Or have I missed the point?
Thank you so much! Your tutorials are super helpful.
Jule,
Glad to see that the tutorials have been helpful.
You can use Levene’s test in this case. If p-value > alpha then you retain the hypothesis that the populations have the same variance (i.e. homogeneity).
Note that you really don’t need to use Levene’s test in this case, since you can always use the t test with unequal variances.
Charles
Hello Charles,
Thank you for your help!
I have one further question then. But I do need to know, if the variance is homoscedastic or heteroscedastic for the implementation of the t-test in excel right? Or is there a difference between the homogeneity of the variance and homoscedastic?
Jule,
They are different terms for the same thing.
Charles
Hi Charles.
i need some help about transformations. at many places i have studied that if
some values in a sample are 0, these can be added with a constant, most appropriately with 0.5 and then be transformed for log transformations mostly, but in my case i have one whole group of the sample, out of 5, which has values 0, equal to control. now if i try square root transformation data still doesnt meet the requirement of homosedasiticity as p value is significant for Levene’s test. and if i add 0.5 to all the values of group of that sample, its mean will be a positive digit, which i think should be zero as the raw data values are all zero for that group. please suggest me if it is fine to add 0.5 to all the values and and get a non zero mean in this situation.
Thanks!
Asad,
If the assumptions for the test you are trying to use are met, then this transformation is fine.
Charles
Hi Charles,
Thanks for your help, yes the assumptions were met for the one way ANOVA after log transformation.
Now i have a kind of similar population, but for that assumptions are not met for homogeneity,even after transformations, while the data is normal. As i studied articles here i can go with Welche’s Anova or kruskal-wallis. But to my understanding these both are used on more than one independent variables whereas i have data comprising of one independant variable with 5 levels (more than 2). Please guide which non parametric test i can use to analyze data in this situation.
Greetings from China.
Hello Asad in China,
Welch’s ANOVA is the better choice compared to Kruskal-Wallis when the homogeneity of variance assumption is not met. Welch’s ANOVA is used with one independent variable (i.e. factor) with 2 or more levels.
Charles
hi
i need help this “LEVENE”, because no see in my excel!! 🙁
Sorry, but I don’t understand your question.
Charles
Hello. I need some help. How can we decide the sig. level for levene test is .01 or .05?
Is there any condition required for both of sig.level?
I don’t know of any hard and fast rule here. I typically use a sig. level of .05 for Levene’s test, but I also take other things into consideration. E.g. is the largest variance more than 3 or 4 times the smallest variance, in which case I am more careful. I am even more careful with unbalanced designs, especially if the smaller group has the larger variance.
Charles
Hello Charles,
I’d just like to say thank you so much for these tutorials. They have helped me very much in my application of statistics, since this is verse area.
I have conducted a Levene’s test and my mean (0.14), median (0.44) and trimmed mean (0.14) results are >0.05. Just to clarify, are these results showing that the homogeneity of the group variances (four groups) assumption has been satisfied (variances are not significantly different from each other) and that Kruskal-Wallis can be used?
The null hypothesis is that the variances are homogeneous, and so p > .05 means that we cannot reject this hypothesis. This indicates that you can use ANOVA. By the way, if the variances were not homogeneous, you should usually look to Welch’s ANOVA rather than Kruskal-Wallis.
Charles
Dear Charles,
To my understanding, t-test and ANOVA required data to be normal distributed and homogeneity of variance.
However, what about paired samples t-test? (151 cases for both group, equal sample size)
Do the paired samples t-test analysis also requires an equal variances as independent samples t-test did?
Vincent,
No. The paired t test is essentially a one sample t test where the single sample consists of the differences between the pairs. Thus there is really only one sample and so no equal variances is needed (or even possible).
Charles
Hi Charles,
I’ve got data that represents forecasts of score under two conditions. I’ve calculated the Forecast Error as the (Forecast-Actual) so I’m left with positive numbers, negative numbers, and a handful of zeros. I’d like to compare the variance under the two conditions and was planning on using the non-parametric Levene’s test. (My data fail the Shapiro-Wilk test for normality.) Are the negative numbers going to cause me a problem? If so, can I transform the Forecast Errors into all positive values and then use the Levene’s test?
Thanks,
Preston
You should be able to use Levene’s test even with data that contains negative and zero values.
Charles
Hello Charles,
Thanks for your pointers after I’d left a comment on your homepage – it’s a massive help.
I have performed a Levene’s test using the Real Statistics Data Analysis Tools, and have found that for the mean test I have a p-value of 0.015146, for the trimmed mean I have a p-value of 0.015146, but for the median test I have a p-value of 0.225464!
So the mean and trimmed test suggest that the null hypothesis is rejected and the homogenity of variances assumption is not satisfied (leading to me using Welch’s test), but the median suggests the opposite? I’m still a little unclear as to which one to use – looking at a histogram plot of all the data in my seven groups indicates it is skewed to the right sort of, so the median p-value is probably the one to use if I’ve understood correctly?
The thing is, my 7 groups are equal in size and the highest variance is about somewhere between 3 and 4 times larger than the group with the lowest variance, so perhaps the single factor ANOVA is ok to use, though I do also have non-normal distribution! The reason I was looking into non-parametric testing in the fist place is that I’d originally just performed an ANOVA in Matlab, which showed significance, but when I followed up with Tukey’s test there was no significance shown between group comparisons, hence I’ve looked deeper into things like variance and distribution, ANOVA robustness and applicable alternatives! It’s been a baptism of fire!
Chris,
It seems surprising to to me that the results from the median test is so much different. This is usually an indication of outliers, which, if so, needs to be dealt with irrespective of which version of Levene’s test you use.
If you send me an Excel file with your data I can check to see what is going on. See Contact Us for the email address.
Charles
Apologies – just seen your reply. I have sent my Excel file to your email – hopefully it will make sense to you.
Best,
Chris
Hi Charles,
One help! Considering-if we are not using the Levene´s test just for satisfying the assumptions for ANOVA, and rather to test the variance behaviour between the samples. Is there any approach similar to post-hoc tests if the Levenes test show any significant difference (p<0.05) between the samples.
If the homogeneity of variances assumption is not met, the usual approach is to use a transformation or Welch’s test.
See the webpage Dealing with heterogeneous Variances.
Charles
Thanks a lot for the response.
So as far as I understand (and please correct me if I am wrong), when the samples(>2) show significant difference in variance, i.e. non-homogeneity between the samples, the dataset must undergo one of the following:
1. some other statistical tests (like Kruskal-Wallis, Welch’s test, etc)
or
2. a transformation for the homogeneity of variances?!
Thanks in advance.!
-Burhan
That is correct, but Welch’s test is better than Kruskal-Wallis for non-homogeneous variances.
Charles
Hi Charles,
in my undergraduate thesis I am investigating 4 groups of which I need to know if there are differences in their variances, and what is the group with the highest variance. The data is not normally distributed, so perhaps it might be best to make the Levene test. But my question is, would it be better to make the Bartlett test transforming my data to a normal distribution??
greeting from Chile!
I would tend to use a test that doesn’t require a transformation, and so I would elect to use Levene’s test. I can’t tell you, however, that there won’t be situations where Bartlett’s test on transformed data wouldn’t give a more accurate result. Greetings to you and others from Chile!
Charles
Hi Charles, is Levenes test still valid for 2 factor ANOVA?
Jon
Jon,
Yes, but this time all the groups must have the same variance. If factor A has m levels and factor B has n levels, then there are m x n groups to consider.
You need to reformat the data to use the LEVENE formula in the Real Statistics Resource Pack. I will make this easier for you in the next release, but for now, you need to use the format for the one-way ANOVA test.
Charles
Hi, is it ok to set the alpha level to something other than .05? I would like to set it to .01
Hi Anj,
Yes you can set alpha to any value between 0 and .5, including .01.
Charles
Chales,
Is same spread (passing Levene test) one of the assumption of ANOVA? If yes, dose this mean an endless loop that to use Levene (which adopts ANOVA), we need firstly prove residual groups are equal in spreads which again needs Levene?
pls forgive me about such junior question…
Thank you,
Daniel,
Yes, a key assumption for ANOVA is that the variances of the different groups are not significantly different. The test is somewhat forgiving, however, since even if the the variance of the group with the highest variance is 3 or 4 times the group with the lowest variance the test should still work ok assuming that the groups are all equal in size. If the groups are not equal in size, then the group with the largest variance should be larger than the group with the smallest variance. The more the situation departs from these constraints the less reliable is the test.
Many statisticians are also discomforted by the fact that to test whether ANOVA is suitable to use yet another ANOVA is required (in the Levene’s test). So your is not such a junior question after all. No infinite loop is required though since probably no one performs another ANOVA to check on the variances in the Levene’s Test.
I suggest that you use Levene’s test, but that you also simply check whether there is a large difference between the variances of the original groups and create box plots to see whether the variances look different. Statistical testing is partially an “art form”.
Charles
hi Chales,
the number “2” in “LEVENE(B6:E13, 2) = 0.90357.” might be a typo? because 2 and 1 generate the same result in this case.
Thanks,
Daniel,
Yes, you are correct. The 2 should actually be -1, since I wanted to use the trimmed mean version of the test. In any case the value of Levene’s test is still the same as for mean version of the test.
Thanks for identifying this problem. I have now changed the website, replacing 2 by -1.
Charles