We present four ways of dealing with models where the variances are not sufficiently homogeneous:
- Non-parametric test: Kruskal-Wallis
- Modified tests: Brown-Forsythe and Welch’s ANOVA test
- Transformations (see below)
On the rest of this webpage, we will look at transformations that can address homogeneity of variance. In particular, we look at the square root and log transformations. For transformations that address normality Transformations to Create Symmetry.
Log transformation for homogeneity of variances
A log transformation can be effective when the standard deviations of the group samples are proportional to the group means. Here a log to any base can be used, although log base 10 and the natural log (i.e. log base e) are the common choices. Since you can’t take the log of a negative number, it may be necessary to use the transformation f(x) = log(x+a) where a is a constant sufficiently large to make sure that all the x + a are positive.
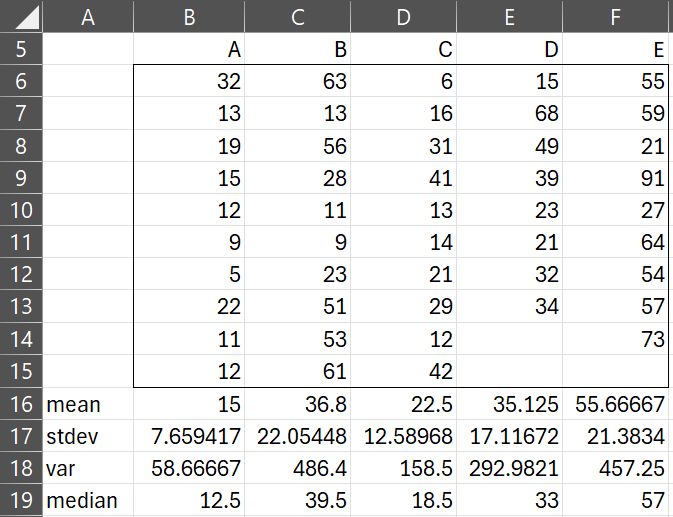
Example 1: In an experiment, the data in Figure 1 were collected. Check that the variances are homogeneous before proceeding with other tests.
Figure 1 – Data for Example 1
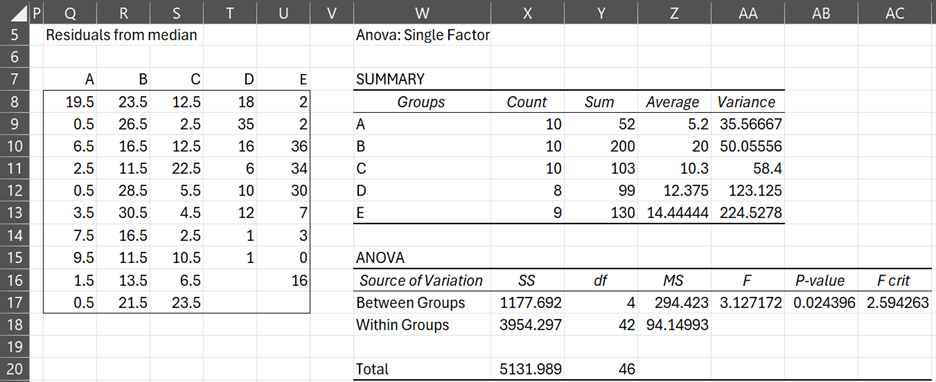
The sample variances in Figure 1 seem quite different. When we perform Levene’s test (Figure 2), we confirm that there is a significant difference between the variances (p-value = 0.024 < .05 = α).
Figure 2 – Levene’s test for data in Example 1
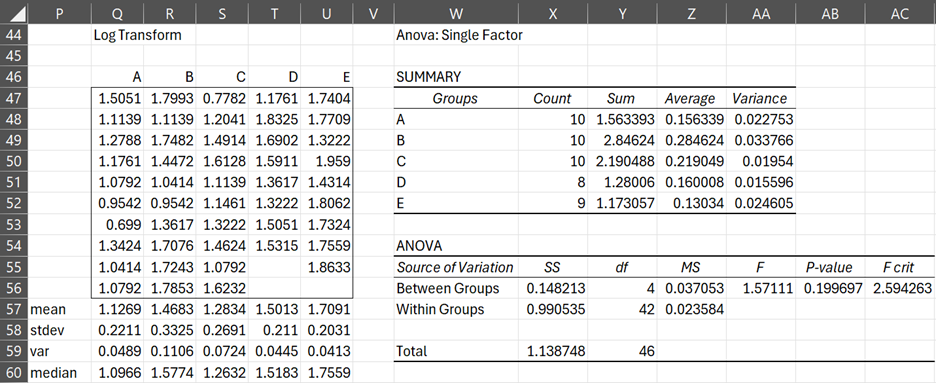
We note there is a correlation between the group means and group standard deviations (r = .88), which leads us to try making a log transformation (here we use base 10) to try to achieve homogeneity of variances (table on the left of Figure 3).
We can see that the variances in the transformed data are more similar. This time Levene’s test (the table on the right of Figure 3) shows that there is no significant difference between the variances (p-value =.20 > .05).
Figure 3 – Log transform and Levene’s test
Square root transformation for homogeneity of variances
When the group means are proportional to the group variances, often a square root transformation is useful. Since you can’t take the square root of a negative number, it may be necessary to use a transformation of form
. Here a is a constant chosen to make sure that all values of x + a are positive. If the values of x are small (e.g. |x| < 10), it might be better to use the transformation
or
+
.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Pelagic Lab (2018) Assessing variance homogeneity
http://www.pelagicos.net/BIOL4090_6090/lectures/Biol4090_6090_Fa18_Lecture13.pdf
Hi Charles, I can’t find evidence of the Levene test in Fig. 2 and 3, only ANOVA Single Factor. Where am I wrong?
Hi Niurka,
Excellent question.
Levene’s test can be performed using the ANOVA Single Factor test on the residuals as described at
Levene’s Test
Cells AB17 in Figure 2 and AB56 in Figure 3 show the results of Levene’s test.
Charles
Hey Charles,
my data are not normally distributed but I have 96 observations, so I was told that over 30 obs. I should not worry about non-normality. However, they are not homogeneous either (p = 0,0009, Levene’s test), so I used the command y1<- log(y + 0.1) to log transform them. After the transformation I get homogeneity (p=0.06683, Levene's test) (but still no normality) and then I perform anova (p=0,000222). These are the results of my Tukey test
$led
diff lwr upr p adj
blue2-blue1 -0.1594835 -2.04058905 1.7216220 0.9961567
blue3-blue1 1.6682217 -0.21288387 3.5493272 0.1011399
control-blue1 -1.6429885 -3.52409401 0.2381171 0.1093253
blue3-blue2 1.8277052 -0.05340036 3.7088107 0.0601372
control-blue2 -1.4835050 -3.36461050 0.3976006 0.1736728
control-blue3 -3.3112101 -5.19231568 -1.4301046 0.0000694
However, before I log transform my data I did Welch's anova (p-value = 8.338e-05) and Kruskal-Wallis (p-value = 0.0002018) and I got the following:
Welch's anova:
$led
diff lwr upr p adj
blue2-blue1 0.8078231 -14.982667 16.598313 0.9991454
blue3-blue1 19.0277778 3.237287 34.818268 0.0113818
control-blue1 -10.2380952 -26.028586 5.552395 0.3329478
blue3-blue2 18.2199546 2.429464 34.010445 0.0168532
control-blue2 -11.0459184 -26.836409 4.744572 0.2671212
control-blue3 -29.2658730 -45.056363 -13.475383 0.0000260
And Kruskal-Wallis:
Comparison Z P.unadj P.adj
1 blue1 – blue2 0.09696247 9.227562e-01 9.227562e-01
2 blue1 – blue3 -2.42637042 1.525070e-02 3.050139e-02
3 blue2 – blue3 -2.52333289 1.162483e-02 3.487449e-02
4 blue1 – control 1.98773067 4.684149e-02 7.026223e-02
5 blue2 – control 1.89076820 5.865529e-02 7.038635e-02
6 blue3 – control 4.41410109 1.014306e-05 6.085834e-05
I get more groups with sign. differences in the non parametric tests and I don't know which test I should trust.
And another thing, after the log transformation my variances look like that:
[1] 3.000720 -2.302585 -2.302585 3.914021 3.691376 -2.302585 -2.302585 2.819393 -2.302585 -2.302585 -2.302585 3.691376
[13] -2.302585 3.691376 -2.302585 -2.302585 -2.302585 3.222868 3.000720 4.201204 -2.302585 -2.302585 2.666236 -2.302585
[25] -2.302585 3.914021 -2.302585 -2.302585 -2.302585 -2.302585 -2.302585 -2.302585 3.914021 -2.302585 -2.302585 -2.302585
[37] -2.302585 -2.302585 -2.302585 2.819393 -2.302585 4.383276 3.000720 3.222868 -2.302585 -2.302585 -2.302585 3.222868
[49] -2.302585 -2.302585 -2.302585 -2.302585 -2.302585 -2.302585 3.914021 -2.302585 3.222868 -2.302585 -2.302585 3.509553
[61] -2.302585 -2.302585 -2.302585 -2.302585 -2.302585 -2.302585 -2.302585 2.819393 4.096010 -2.302585 -2.302585 3.509553
[73] 3.914021 3.914021 3.222868 3.000720 -2.302585 -2.302585 3.222868 -2.302585 3.914021 3.000720 -2.302585 -2.302585
[85] 4.318821 -2.302585 -2.302585 -2.302585 4.606170 4.606170 3.509553 4.096010 -2.302585 -2.302585 -2.302585 -2.302585
[97] 3.222868 2.819393 -2.302585 3.509553 -2.302585 3.222868 3.222868 4.096010 3.796487 3.000720 3.914021 4.606170
[109] 2.819393 -2.302585 -2.302585 -2.302585
Does the fact that I have negative values mean that my transformation is wrong?
Thanks
Hello Maria,
1. From the central limit theorem, generally large samples will be normally distributed. But there is no guarantee that such a sample is indeed normally distributed, and so you should check this in any case.
2. Since it looks like you have 4 groups, if the groups are of the same size, each sample has 96/4 = 24 elements. Note that you need to check that each group is normally distributed.
3. If the homogeneity of variances assumption is violated, ANOVA is probably not the right choice. Kruskal-Wallis is also not a good choice. If the data are normally distributed (or not too far away from normality), then Welch’s ANOVA could be a good choice (even without a log transformation).
4. If the data after transformation is reasonably normally distributed, then ANOVA might be appropriate (since you say that the homogeneity of variance assumption is met). Remember too that ANOVA is pretty robust to violations of normality. If, however, the data of one or more of the groups is quite skewed (and so the normality assumption is strongly violated), then Kruskal-Wallis could be a good choice.
5. The various approaches all work even with negative data.
Charles
Thank you Sir for the detailed information you provide. I need guidance on this….
I have 2 treatment groups to compare with a control group, pretest-posttest. T1 vs Control, T2 vs Control and T1 vs T1, to determine any statistical significant differences.
I am confused whether to do ANCOVA or MANOVA…help me out with it please.
Homogeneity of variance and homogeneity if regression slopes is violated for ANCOVA, how do I correct that or what are the alternative tests to adopt? Thank you.
Nana,
If you satisfy the assumptions for ANOVA repeated measures with one between-subjects factor (treatment and control groups) and one within-subjects factor (pretest vs posttest) you can use that approach. If you satisfy the assumptions of MANOVA you can also use that approach. If you are only testing whether posttest minus pretest is significant you can use one-way ANOVA.
Since the equal slopes assumption is violated it appears that ANCOVA is not appropriate.
Charles
Hi Mr.
I have five experimental groups (all groups 24 subjects). I try many transformations and assumptions of normality and equal variances are not met.
Can I use Welch’s ANOVA or Kruskal-wallis test to compare the groups? other test?
thanks!
Welch’s ANOVA is probably the better choice since equal variances is much more important than non-normality. How far from normality is the data? How far from homogeneity of variances is the data?
Charles
Thanks Charles!. for four groups:
Levene´s test from means p (same): 5,10E-07
Levene´s test from medians p (same): 0,0001195
A B C D
N 24 24 24 24
S-W W 0,9119 0,7367 0,3929 0,4587
p(normal) 0,03875 3,21E-05 5,97E-09 2,29E-08
Hello Diego,
Yes, both assumptions are heavily violated. Which test to use is therefore less clear. You could use a resampling approach. Alternatively, see
https://scialert.net/fulltext/?doi=jas.2004.38.42
Charles
Thanks for your time!
I am comparing three experimental groups (Group 1 has 16 subjects, group 2 has 53 and group 3 has 2 subjects) using one-way ANOVA. However, assumptions of normality and equal variances are not met. Should I use Welch’s ANOVA or Kruskal-wallis test to compare the groups now?
Hello Sarah,
If normality is not violated too badly, then Welch’s ANOVA is likely to be the better choice since ANOVA is more robust to violations of normality than equal variances. Not so clear how good the result will be with only 2 subjects in group 3 though. I would put more trust in the follow-up test: Games-Howell is the likely choice. Another approach is to use bootstrapping.
Charles
Thank you so much for your quick response. I performed Welch ANOVA, and there was no significant difference among the groups.
Dear Mr.Zaiontz,
First Thanks a lot for you very useful website, great job.
I have 6 independent groups of data with equal sizes and I want to apply ANOVA test to see if there is any significant differences among these groups or not. I check the data for assumptions for ANOVA and because two groups were not normally distributed I used a log transformation to normality and accordingly I used the transformation for other 4 groups otherwise the scale of data would be so different, so all groups are now normally distributed. However homogeneity of variance test in ANOVA showed the variances are not sufficiently homogeneous even after transformation? I would be so grateful if you tell me what should I do now?
I tried to do Z-score transformation of course the data have all assumptions for ANOVA but there is no differences among group anymore.
Parisa,
Welch’s ANOVA test is probably the best option. See the following webpage:
Welch’s ANOVA
Charles
Thank you very much:))
hi charles i have seen your website and it remarkable and educative. i have one independent variable(treatment) which have 12 cases with in it and more than 5 dependent variables like plot cover , vigorsity ,number of pod per plant and other parameters. i would try to normalize my data and then after i have checked homogeinety of variance, but some of my data’s(dependent) are significant and other are not significant i.e; pvalue >0.05 what shall i do?
Shambel,
I don’t really have a complete picture of the scenario that you are investigating, but there isn’t anything wrong with having some significant results and some non-significant results. If these results relate to homogeneity of variances, then you may be able to perform some test for certain dependent variables, but not for others (or use a non-parametric test for these).
When you have multiple dependent variables, it usually better to perform MANOVA instead of separate ANOVA’s.
Charles
I am comparing the difference in structural attributes (i.e., snags, live trees, and coarse woody debris) among managed stands, natural (~140-yr-old) stands, and natural (~500-yr-old) stands.
For snags (stems, dbh, and height) and CWD(pieces and diameter) I was able to use one-way ANOVA (all assumptions were met). HOWEVER, for live trees (stems, dbh, and broken top count) I cannot meet the one-way ANOVA assumptions (i’ve tried transforming the data). I was thinking of using the Brown-Forsythe test with a post-hoc (still don’t know which one to use).
However, can I report some attributes with one-way ANOVA and some with Brown-Forsythe test? If I’m summarizing my statistical results in a table (mean, SE, 95%CI, F value and P-value), do i asterisk (*) the 3 tests that failed the homogeneity of variance assumption and therefore I had to use Forsythe-brown test?
Victoria,
If the one-way ANOVA is applicable for one hypothesis and Brown-Forsythe is applicable for a different hypothesis (or for a similar hypothesis using different data), then you can report the results from both tests.
In general Welch’s ANOVA is a better test than Brown-Forsythe when the homogeneity of variances assumption doesn’t hold.
Charles
Hi,
I am trying to analyze the interaction of two factors using two-factor mixed ANOVA (with repeated measures on one factor). However, since my data violates the assumption of homogeneity of variances (Levene’s test) , mixed-ANOVA seems to be not the best option.I tried to use transformations, but I’ve read a few papers about how transformations can sometimes yield misleading results. It seems like I need to run Scheirer Ray Hare analysis instead. However, is this analysis able to consider the fact that there was one within-subjects and one between-subjects factor?
Thanks!
Jason,
Scheirer Ray Hare assumes that both factors are not repeated measures.
Charles
Thank you Sir for your post. But I have a question. How to determine/calculate/analyze post hoc test after we use Scheirer-Ray-Hare Test? (I have red your “Scheirer-Ray-Hare Test” post, but I cant’t write my comment/answer on that post, so I write in here, hhe)
Thank you (I’m sorry if my english is bad)
Fauzi,
You can use any of the follow-up tests to Kruskal-Wallis provided the assumptions for that test are met. You can also use the Mann-Whitney test perhaps using a Bonferroni correction.
Charles
Thank’s Sir
Hi Sir,
My study is about comparing two sources of larvae (hatchery and wild) with survival as the dependent variable. I want to use 2 way ANOVA to see if there is any interaction between them, however, it does not satisfy the levene’s test requirement even after I log transformed my data. Should i just proceed with 2 way ANOVA?
My second question is not related to the above question. A friend told me that when Levene’s test failed in 1 way ANOVA, first transform it,if it is already homogenous proceed then to the 1 way ANOVA. However if it is still not homogenous, I must use kruskal -wallis test instead of 1 way ANOVA. Is this correct?
Thank you..
Jean,
1. There are other transformations that you can use besides the log transformation. I will soon add support for Box-Cox transformations. Another option is to use Scheirer-Ray-Hare ANOVA.
2. If homogeneity of variance test fails then you are probably better off using Welch’s ANOVA.
Charles
Dear Charles,
Thank you for your very insightful website.I was hoping you could provide me with some more specific advice. I am currently running a GLM with one factor (sex) and 4 covariates (three are constant, for the other one I have 8 alternatives I am interested in, so I am running 8 GLM’s) on a single DV. My sample size is 347(197 females; 150 males). Levene’s test indicates significant inhomogeneity of variance (p-values ranging from .033 – .048). The larger variance is in the smaller group (males), with the std. deviations being .81 for females and 1.00 for males. Transformations do not ameliorate the inhomogeneity of variance. I have read that GLM becomes too liberal when there is larger variance in the larger group, and since I do not find any significant effects with the current analysis, is it valid to report, based on this analysis, that there are no valid effects?
Thanks in advance,
Best,
Niels
Niels,
The case where the larger variance is in the smaller group is the one that is most troublesome. Levene’s test is somewhat borderline, especially the p-value = .048. When you say that Levene’s test is .033 – .048, are you running multiple versions of Levene’s test on the same data or tests on multiple collections of data?
If you really have a problem with heterogeneity of variances and you can’t find a suitable transformation, then you can either use a different test which doesn’t require homogeneity of variance (e.g. Welch’s ANOVA instead of the standard ANOVA) if such a test exists or you can report your results but make sure that you explain that there is a potential problem with homogeneity of variances.
Charles
Hi Dr Charles,
I have two variables by different variances and i want equalizing variances by transformation.
I use this method:
***In plain English, to transform a variable to have a desired mean and a desired standard deviation, simply take the Z-transform of the original variable, multiply it by the desired standard deviation, and then add the desired mean.***
But in paper “Experience with using Ellenberg’s R indicator values in Slovakia: oligotrophic and mesotrophic submontane broad-leaved forests” in Appendix 1. Rc(resc) variable (by equalizing variance transformation base on Re(2-8)) is different with my numbers that obtain by above method, (diffrent between numbers is most 0.15), Dr. please help me
Thanks
Hi Masoud,
This transformation will clearly create two new variable with equal variance, but depending on what you are trying to do with the data this may or may not be useful. What sort of hypothesis are you testing?
Charles
Sir, after using the log tranformation my data is homogenous so i want to use two way anova analysis. In that analysis, should i use the data that has been transformed or the original data? Thank you
You should use the transformed data since it satisfies the ANOVA assumption. Keep in mind that your conclusions related to the transformed data, and you need to determine how this maps into the original data (and the population from which is comes).
Charles
hi
sir
I have to employ factorial anova on my data where in I have two categorical independent variables and two continuous dependent variables. it would be a gain score (post-pretest) analysis. I checked homogeneity of variances for posttest scores and they are not homogenous. I thought to do log transformation
however I am confound if I can do log transformation on my posttest score or should I do it on a gain score? please tell me
Thanks in advance
When you say that the variances for the posttest scores are not homogeneous, does this mean that there are multiple posttest scores? If not, then I don’t know what this means.
In any case, you can apply a transformation on any of variable(s) that you choose. It sounds like your goal is to choose whichever variable(s) for the homogeneity of variances assumption. I would try both choices and see whether either one yields homogeneous variances.
Charles
Charles
many thanks for your precious response.
yeah, there are three levels of this independent variable. I did levenes test on post test scores of these three groups and these are not homogenous.
Hence, I had to say if I should transform data on posttest scores or on gain scores.
thanks in advance
I am not sure what you mean by gain scores. Are these each of the three posttest scores minus a baseline score (aka a pretest score)? If so I would try a transformation on both and see which one works better.
Charles
yeah. gain I mean is posttest -pretest.
Thanks a lot indeed for your response.
And for clarifying my query. 🙂