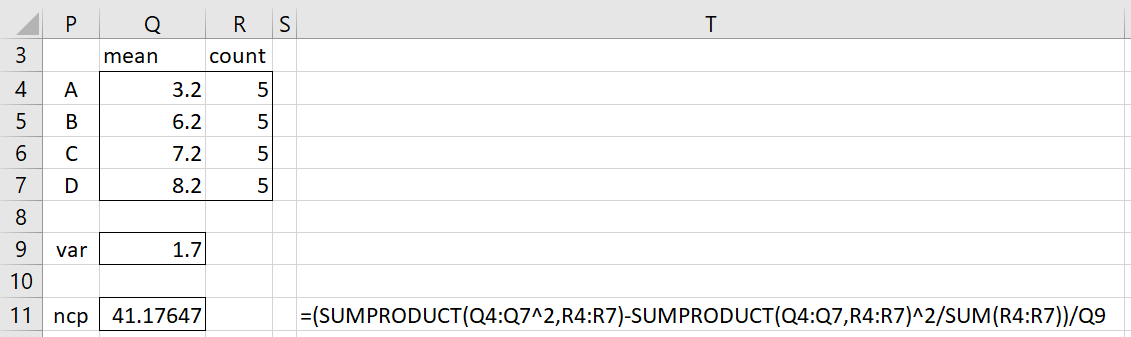
To calculate the non-centrality parameter, required for estimating the power of a one-way ANOVA, we need to estimate the means and the number of replications for each of the treatment groups and the variance for each group (assuming homogeneity of variances). This is demonstrated in Figure 1.
Figure 1– Estimating the noncentrality parameter
The estimated NCP is given in cell Q11. If instead, you needed to estimate Cohen’s f, you would divide this value by the sample size, 20 in this case, and then take the square root. For the example in Figure 1, this would result in f =1.43486.
Example
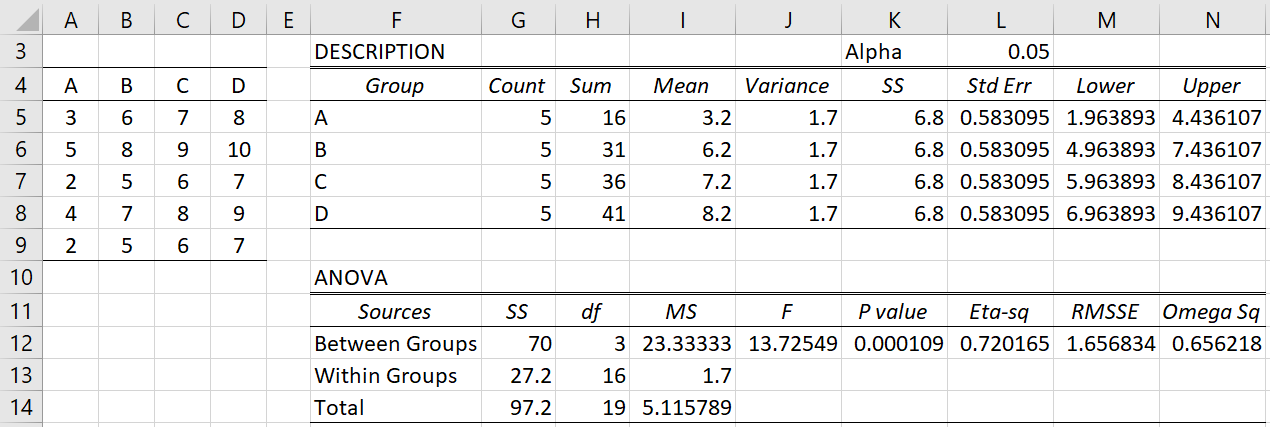
The one-way ANOVA model displayed in Figure 2 for the data in range A4:D9 has the characteristics shown in Figure 1.
Figure 2 – One-way ANOVA
Note that the non-centrality parameter can be calculated by the formula =G12/I13, i.e. by SSB/MSE = 70/1.7 = 41.17647, which is the same result we obtained in cell Q11 of Figure 1.
Worksheet Function
Real Statistics Function: The Real Statistics Pack provides the following function for calculating an estimate of the non-centrality parameter for one-way ANOVA.
NCP_ANOVA(R1, R2, v) = the non-centrality parameter of a one-way ANOVA for group means specified in the column array R1 where the number of replications for each group is specified in column array R2 and the variance for any of the groups is v.
Note that R2 can be replaced by a single positive integer value, in which case each of the groups is assumed to be replicated by this value.
The NCP estimate shown in Figure 1 can be calculated by placing the formula =NCP_ANOVA(Q4:Q7,R4:R7,Q9) or =NCP_ANOVA(Q4:Q7,R4,Q9) in cell Q11.
Observation
If each of the groups is replicated the same number of times and we only can estimate the maximum difference between any two group means, then we can estimate NCP by m*d^2/(2*v) where m = # of replications per group, v = the variance for each group and d = the biggest difference in the means between groups.
Essentially this assumes that means for the groups that are not farthest apart are halfway between these extreme group means. The NCP_ANOVA function can be used for this purpose where R1 and R2 are instead single values, i.e.
NCP_ANOVA(d, m, v) = the non-centrality parameter of a one-way ANOVA where d = the largest difference between group means, m = the number of replications for each group and v = the variance for any of the groups.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
O’Neill, M. & Thomson, P. (1998) Spreadsheet for calculating one-way ANOVA
https://www.stats.net.au/resources.htm