Truncated Normal Distribution

Basic Concepts

Definition 1: Let -∞ ≤ a < b ≤ ∞. Then the pdf of the truncated normal distribution with mean μ and variance σ2 constrained by a ≤ x ≤ b is

Truncated normal pdf

where φ is the pdf of the normal distribution and Φ is the cdf of the normal distribution.

We assume that if x < a or x = -∞ then φ(x, µ, σ) = 0 and Φ(x, µ, σ) = 0. If x > b or x = ∞ then φ(x, µ, σ) = 0 and Φ(x, µ, σ) = 1.

Thus, in Excel, if a and b are finite then

f(x) = NORM.DIST(x, µ, σ, FALSE)/(NORM.DIST(b, µ, σ) – NORM.DIST(a, µ, σ))

The cdf of this distribution is

Truncated norml cdf

The inverse distribution function is

Inverse truncated normal function

Properties

We now present some key statistical properties, but first we define

d_k

Here, we assume that if b = ∞ then Φ(b, µ, σ) = 1 and (b–µ)kφ(b, µ, σ) = 0. Similarly, if a = -∞ then Φ(a, µ, σ) = 0 and (a–µ)kφ(a, µ, σ) = 0.

Mean

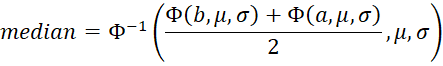
Median truncated normal

Mode

Variance

Skewness

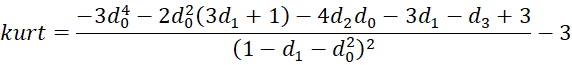
Kurtosis

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack provides the following functions.

TNORM_DIST(x, μ, σ, cum, a, b) = the probability density function value f(x) for the truncated normal distribution N(μ, σ2, a, b) when cum = FALSE and the corresponding cumulative distribution function F(x) when cum = TRUE.

TNORM_INV(p, μ, σ, a, b) = the value x such that TNORM_DIST(x, μ, σ, TRUE, a, b) = p, i.e. inverse of TNORM_DIST(x, μ, σ, TRUE, a, b).

TNORM_PARAM(μ, σ, a, b, lab): array function that returns a column array with the following parameters for the truncated normal distribution N(μ, σ2, a, b): mean, median, mode, variance, skewness, kurtosis.

If a is omitted then it defaults to -∞, while if b is omitted then it defaults to ∞. If lab = TRUE (default FALSE), then an extra column of labels is appended to the output.

Note that you can use the following Excel formula instead of  TNORM_INV(p,m,s).

=NORM.INV(p*(NORM.DIST(b,m,s)-NORM.DIST(a,m,s))+NORM.DIST(a,m,s),m,s)

References

NtRAND (2020) Truncated normal distribution
https://www.ntrand.com/truncated-normal-distribution/

Burkardt, J (2014) The truncated normal distribution. Florida State University
https://people.sc.fsu.edu/~jburkardt/presentations/truncated_normal.pdf

Cha, J (2015) Re-Establishing the theoretical foundations of a truncated normal distribution: standardization statistical inference, and convolution. Dissertation at Clemson University
https://tigerprints.clemson.edu/all_dissertations/1793

12 thoughts on “Truncated Normal Distribution”

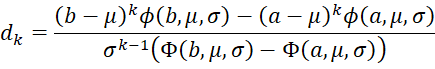
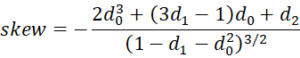
  1. IS THERE A POSSIBILITY TO IMPLEMENT THE GHK ALGORITHM TO ESTIMATE MULTIVARIATE PROBABILITIES OF A MULTIVARIATE NORMAL FUNCTION?

    Reply

Leave a Comment