Basic Concepts
Definition 1: A random variable x is log-normally distributed provided the natural log of x, ln x, is normally distributed. See Exponentials and Logs and Built-in Excel Functions for a description of the natural log. The probability density function (pdf) of the log-normal distribution is
Properties
Some key statistical properties are:
The coefficient of variation is
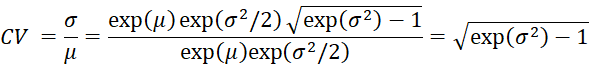
As described in Transformations, sometimes it is useful to use a transformation of the population being studied. In particular, since the normal distribution has very desirable properties, transforming a random variable into a variable that is normally distributed by taking the natural log can be useful.
Chart
Figure 1 shows a chart of the log-normal distribution with mean 0 and standard deviations 1, .5 and .25.
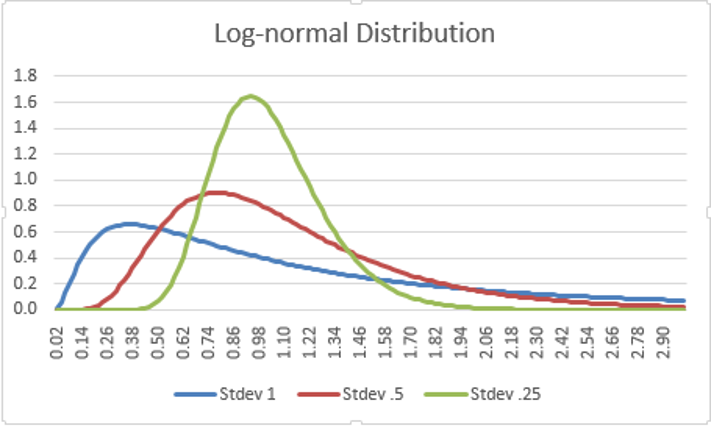
Figure 1 – Chart of Log-normal Distribution
Note that the log-normal distribution is not symmetric, but is skewed to the right. If you have data that is skewed to the right that fits the log-normal distribution, you may be able to access various tests described elsewhere on this website that require data to be normally distributed.
Worksheet Functions
Excel Functions: Excel provides the following two functions:
LOGNORM.DIST(x, μ, σ, cum) = the log-normal cumulative distribution function with mean μ and standard deviation σ at x if cum = TRUE and the probability density function of the log-normal distribution if cum = FALSE.
LOGNORM.INV(p, μ, σ) = the inverse of LOGNORM.DIST(x, μ, σ, TRUE)
Note that:
LOGNORM.DIST(x, μ, σ, TRUE) = NORM.DIST(LN(x), μ, σ, TRUE)
LOGNORM.DIST(x, μ, σ, FALSE) = NORM.DIST(LN(x), μ, σ, FALSE)/x
LOGNORM.INV(p, μ, σ) = EXP(NORM.INV(p, μ, σ))
These functions are not available in versions of Excel prior to Excel 2010. Instead, these versions of Excel use LOGNORMDIST(x, μ, σ), which is equivalent to LOGNORM.DIST(x, μ, σ, TRUE), and LOGINV(p, μ, σ), which is equivalent to LOGNORM.INV(p, μ, σ). For the pdf function, the formula equivalent to LOGNORM.DIST(x, μ, σ, FALSE) is NORMDIST(LN(x), μ, σ, FALSE)/x.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
Wikipedia (2013) Log-normal distribution
https://en.wikipedia.org/wiki/Log-normal_distribution
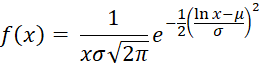
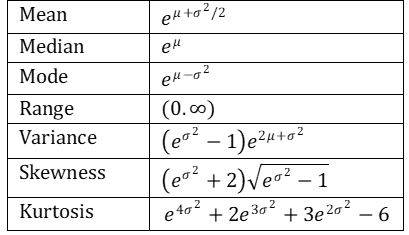
Simple, efficient and knowledgeable explanation, thanks for everything!
Greetings Charles !
Asim from Bihac, Bosnia, Sept. 2023
Hello Asim,
Glad I could help and greetings to people in Bosnia.
Charles
If I only have a single point on a lognormal curve – not the mean – but I know it’s probability, and I know the standard deviation of the curve, how can I find the median value?
Hello Evan,
1. Suppose that you know that a particular point (x, f(x)) lies on the lognormal curve and you know the value of sigma. You need to find the value of mu. Once you know the value of mu, you know from the table on the webpage that the median is exp(mu).
2. By way of illustration, suppose that the point on the curve is (3, .013253) and sigma = 5. You can use Excel’s Solver to estimate the value of mu. This can be done by placing the formula =LOGNORM.DIST(3,A1,5,FALSE) in cell A2 and some initial guess for mu in cell A1 (e.g. 4). Now on the Solver dialog box, insert A2 in the Set Objective field, choose the Value Of option and insert the value .013253 in the box next to this option. Finally, you need to insert A1 in the By Changing Variable Cells field.
When you click on the Solve button, you should get a value near 7 in cell A1, which means that mu = 7. If you insert the formula =EXP(A1) in cell A3, you should see the value of the median, namely 1096.633, in cell A3.
3. If instead of knowing the value of sigma, you know the value of the standard deviation of the distribution, then things are slightly more complicated, although you should still be able to use Solver. Let’s suppose that the standard deviation is 2.
This time you have two unknown values, mu and sigma, and a constraint. Let’s use B1 to hold sigma and B2 to hold the constraint. We can insert an initial value of say 5 in cell B1 and place the formula =SQRT(EXP(B1^2-1)*EXP(2*A1+B1^2)) in cell B2. This is the formula for the standard deviation as shown on the table on the webpage. Also, you need to change the formula in cell A2 to =LOGNORM.DIST(3,A1,B1,FALSE).
As before, on the Solver dialog box, insert A2 in the Set Objective field, choose the Value Of option and insert the value .013253 in the box next to this option. Now insert the range A1:B1 in the By Changing Variable Cells field. Next, click on the Add button in the Subject to Constraints part of the dialog box and insert the constraint B2 = 2. Finally, click on the Solve button.
I hope this works since I haven’t tried it out myself.
Charles
Charles,
If the distribution is a log-normal distribution, all of the values need to be >1. So, may I ask you do we have to transform all the variables before using the LOG.NORM functions in excel? Or can we use the historical observations NOT TRANSFORMING THEM and just simply input them into excel? Thank you, Jason
Hello Jason,
I am sorry, but I don’t understand your question.
First of all, all the values need to be positive and not >1.
Have you tried using the historical observations without transforming them?
Charles
Hi Charles,
I have a point on the CDF (age, cumul_pct) and the standard deviation, and I’m trying to use numerical methods to find the mean.
When I look at Wikipedia, there are two formulas:
The Phi equation: F(x) = cumul_pct = PHI((LN(age)-LN(mean))/LN(stand_dev))
The erf equation: F(x) = cumul_pct = 1/2*(1+ERF.PRECISE((ln(age) – ln(mean)) / (ln(std_dev) * sqrt(2))))
However, for the same mean, I’m getting different cumul_pct.
I’m not sure what I’m doing wrong.
Can you help?
There’s a third equation that seems to give me “good” results is:
The norm equation: F(x) = cumul_pct =NORM.DIST(LN(age),LN(mean),LN(std_dev),TRUE)
Why does this seem to give correct results but not the two others?
Andrew,
This version should give the correct results. I have not used the other versions but see my previous response.
Charles
HI Andrew,
If you email me an Excel file with your calculations, I will try to figure out what is going wrong.
Charles
Hi Charles,
I’m trying to analyze benchmark interest rates (1mo T-bill up to 30yr gov’t bond) to understand the probability of each x value in cumulative and non-cumulative terms. They seem to be generally lognormal but some of the x values are 0 (and may be negative depending on the country being analyzed). So, I keep getting the #NUM error when using excel and I have been searching for a workaround, but to no avail. I need the following:
1. Excel formula to calculate non-cumulative probability for each x value
2. Excel formula to calculate cumulative probability for each x value
It looks like you are quite knowledgeable here so wanted to ask given a few hours of searching has yielded no solutions. I’m semi-new to this and trying to understand how to work with interest rate data and probability.
Appreciate any help you may be able to offer.
Drew,
Putting aside the issue of x values that are not positive, the Excel function LOGNORM.DIST provides both the pdf (non-cumulative probability) and cdf (cumulative probability). Now, what to do with x <= 0? One approach is to add a fixed positive value to all the x values so that you can use LOGNORM.DIST. This is especially attractive if the smallest negative value is not so large in absolute value compared to the other x values. E.g. suppose that your smallest negative value is x = -.1, then you can add .11 (or any value larger than .1) to all the x values and then use the LOGNORM.DIST function. Charles
Thank you so much Charles. It seems so simple but never even thought about something like this. Appreciate the help.
Hi Sir,
I have a question.
Produce 10000 lognormal distributed random variables with parameter, (mu, sigma2) = (0,0.625). Compare analytical and simulated pdf
How to generate 10000 log normal RV?
Thanks
Mukesh
Hi Mukesh,
The following formula will generate one random value. =LOGNORM.INV(RAND(),mu,sigma)
You can enter this formula in cell A1, highlight range A1:A10000 and press Ctrl-D to get 10,000 such values.
Charles
sir, plz tell me that how to calculate mean, standard deviation and what is x here , in case of lognormal distribution
You don’t calculate x. x is the input value. You calculate the value of the pdf and cdf based on x.
If you know the values of the mu and sigma parameters, then using the formulas on this webpage you can calculate the mean and standard deviation.
Charles
Sorry, Charles. I meant the mode (0.57) not the median of a a lognormal distribution with known 5% (0.4) and 95% (0.8) quantiles to generate 100 lognormal random numbers.
Mike,
If you know the mu and sigma values of the lognormal distribution, you can generate 100 random values using the formula =LOGNORM.INV(RAND(),mu,sigma)
As can be seen on this webpage, the mode can be calculated by the formula =EXP(mu-sigma^2)
The 5% quantile can be calculated by =LOGNORM.INV(.05,mu, sigma) and the 95% quantile can be calculated by =LOGNORM.INV(.95,mu, sigma).
You have an overconstrained problem (two unknowns mu and sigma, but three equations).
You can use Solver to find the “best” estimates of mu and sigma. The answer will depend on how you define best. One approach is to minimize the sum of the squared errors.
I will email you a spreadsheet that carries out this approach.
Charles
Thanks a lot, Charles! I saw the spreadsheet and it makes perfect sense using Solver to get approximate values for mu and sigma given that I know the mode and quantiles.
Again, thanks for your swift reply and the worked example!
Hello, Charles.
I have the median (0.57) , 5% quantile (0.4) and 95% quantile (0.8) of a lognormal distribution. How can I generate 100 random lognormal numbers with that information?
Thanks!
Hello Charles
I have data for the tensile strength of a material. I was only given 4 values
The average= 3200 ,
the minimum = 2900,
5% fractile = 3000,
95% fractile =3900
If I assume a LogNormal distrubution how can i calculate the Cov and standard deviation.
Thanks you in advance
Hello Almo,
If you knew the mean and median, you could use the formulas on this webpage to calculate the mu and sigma values, and from these, you could calculate the variance (again using a formula on this webpage) and from this the standard deviation. I don’t know what you mean by the Cov.
Since you don’t have the median, I tried to use Solver to calculate the values of mu and sigma that produce the values for the mean (using the formula on the webpage) and the values for the 5% and 96% percentile (using the formulas =LOGNORM.INV(.05,mu,sigma) and =LOGNORM.INV(.95,mu,sigma). I found that Solver doesn’t converge to a solution, or even close to a solution, unless reasonable initial guesses are made for mu and sigma. The best values I found were mu = 8.11427690172921 and sigma = 0.0828114901083954. These produce values for the mean of 3353.32, 5% percentile of 2916.28 and 95% percentile of 3829.50. This also produces a standard deviation of 278.17.
Charles
Greetings Dr. Charles,
I have a question, if you don’t mind!
I am trying to calculate Sauter Mean using log-normally distributed data with the following parameters:
u = -2.22 um
σ = 0.43
Particle diameters range : 0.5 um – 300 um
So, my question is how to correctly substitute the values with the mean being negative?
The distribution is rather confusing, particularity when I learned that one is occasionally given either a “standard deviation” or “geometric standard deviation” without clear specification!
I am not familiar with the Sauter mean. Perhaps one of these webpages will be helpful:
https://www.researchgate.net/post/What_is_the_formula_to_relate_the_Sauter_mean_diameter_to_the_mean_or_median_and_standard_deviation_of_a_log_2_normal_weighted_distribution
https://en.wikipedia.org/wiki/Sauter_mean_diameter
Charles
I’m trying to model (via monte carlo simulation) returns on an options strategy that I know will follow a lognormal distribution. I also know that it is impossible to have a negative return on the strategy for a given week’s return, so all values must be possible. The mean and std deviation are generated on a running basis from live data (as I perform week to week), taking the ln of the returns and solving for the mean and std dev from that. The problem is that when I execute the LOGNORM.INV(RAND(), m, std) for the cells, I still get very negative numbers, and the distribution appears to be normal.
Any suggestions on how I can model the performance?
Thanks
Elliot,
Perhaps I am not understanding the situation properly, but I thought that LOGNORM.INV(p,m,s) is always non-negative and so I don’t see how you are getting negative values.
Charles
Hi ALL!
Im have a mean and a standard divuation for what i know to be a lognormal distribution. I need to find 2000 times different random variables for that distribution and I have two questions.
1)LOGNORM.INV(RAND(),MEAN,STANDARDDIV) – Im using thus formula to getenrate the random variable but it is giving me absurd high number 0f 300450 when my mean number is 20… do you know how to solve this?
2) How can I generate 2000 randome variables or make a forumla choose each time a different random variable? Manythanks
Hello Sofia,
If you know the mu and sigma parameters then, =LOGNORM.INV(RAND(),mu,sigma) is the correct way to generate a random value from this distribution and so 300450 could be a valid random number. The problem may be that mu and sigma are not the mean and standard deviations of the lognormal distribution. You can see this from the table of distribution properties on this webpage (the first Observation). To find the values of mu and sigma from the sample mean and standard deviation, see the following webpage:
Method of Moments: Lognormal Distribution
Charles
Hi, so i have this information that service time is distributed lognormally with the expression 3 + LOGN (23, 33.7). I’d like to generate random number for simulation but the numbers do not make sense. any idea how i should solve this?
Jennifer,
If the mu and sigma parameters are 23 and 33.7, then you should be able to generate random values by using the Excel formula =3+LOGNORM.INV(RAND(),23,33.7)
Charles
Hi Charles.
I have this set of values, min=.05,most likely=.06 and max=.12. We applied LN(x) for each number to get the mean and std. when used with this formula – lognorm(rand(),m,s) i am getting values that is higher than my supposed max value of .12. Is our calcualtion correct or are we still missing some computation steps? How do I limit the max values so that it does not exceed the .12 value? Thanks for this website, very informative by the way.
Best
Hi Poginier,
Glad that you are getting value from the website.
Since the log-normal distribution doesn’t have a maximum value, the only way I know of restricting values over .12 is to simply eliminate any value over .12.
Charles
Please how can I plot a log normal graph using excel 2007?
Figure 1 of https://real-statistics.com/normal-distribution/basic-characteristics-normal-distribution/ shows how to plot the normal distribution. The plot of the log normal distribution is done in the same way, except that you need to use the Excel function LOGNORMDIST instead of NORMDIST.
Charles
Hey Charles,
I have a Monte Carlo Situation of fitting the interest data of mortgage loan over five years that I have collected. I tried the fitting distribution method of assessing the data as normalised, but the chi-test failed. I’m assuming the data is lognormalised, like most of the interest data tend to be. Is there a method for proving my hypothesis of the data being lognormal and a random number generator that generates random values considering it is a lognormal distribution.
Rohit,
1. Assuming that you data is in column A, say in the range A1:A100. Enter the formula =LN(A1) in cell B1, highlight the range B1:B100 and press Ctrl-D. Now apply any of the normality tests on the data in column B. I recommend that you use Shapiro-Wilk.
2. To generate a random number that follows a lognormal distribution with mean m and standard deviation s, use the formula =LOGNORM.INV(RAND(),m,s).
Charles
Hello,
I got values with LOGNORM.INV(RAND(),m,s);
s=SQRT(LN(1+25.6^2/57.3^2)) and m= LN(57.3)-0.5*sigma^2. But i have to use normal values after this calculation. How can i get normal values? Because i think i got z values which means z=(Inx-m)/s???
Sinsin,
I am sorry, but I don’t understand what you mean by “how can I get the normal values?”.
You can transform a value that follows a lognormal distribution to a normal distribution by using the function f(x) = EXP(x). Thus if the value from LOGNORM.INV(RAND(),m,s) were say 2, then the normal transformation would yield the value EXP(2) = 7.389.
Charles
Hey can someone tell me what is the use of ‘x’ in generating data following log normal distribution?
If I want to model for some losses which is random variable ‘x’ then how do I apply the formula?
The main thing is that I want to generate some data following log normal distribution then what should I do?
Yashasvi,
To generate random data that follows the log normal distribution with mean m and standard deviation s, use the formula =LOGNORM.INV(RAND(),m,s)
Charles
Suggestion to Brian. If you use LOGINV(RAND(),3.9573,0.4266) you will get the distribution you want. As a first approximation, you can use LN(mean) and LN(stdev) in place of mean and stdev, but it is not quite correct. The sigma for the lognormal distribution is SQRT(LN(1+25.6^2/57.3^2)) and the mu is LN(57.3)-0.5*sigma^2. This is how the numbers above were calculated.
Hello Charles, I’ve been researching this question on the web for several hours, but I can’t find a good answer. Basically, what I want to do is use Excel to generate 300 numbers with a right-skewed distribution that have a mean of 57.3 and standard deviation of 25.6. Ideally, there would be a parameter that controls the amount of skewness. Is there anything you could suggest to achieve this?
Brian,
You can use the formula LOGNORM.INV(RAND(),57.3,25.6) 300 times. Changing the value of the standard deviation will change the skewness.
Charles
Charles,
Thank you so much for the reply. I tried the formula as given, but most numbers generated were very large, such as 3.63754E+22. Not sure what I’m doing wrong.
Brian
Brian,
You aren’t doing anything wrong. Based on the values for the mean and standard deviation that you chose, the values for the lognormal distribution are large. If this doesn’t serve your purposes you will need to choose a different distribution.
Charles
Thanks again Charles. I will look for a different method as the Lognormal distribution doesn’t seem appropriate for this situation.
Thank you for the excellent website.
Brian
Brian, how did you solve that please?
What approach do you use to transform data which may have zero as a value. e.g. Just ignore them, or add a constant to force all value positive or what?
I would add a constant to force all the value to be positive.
Charles
I made this test (add a constant). The value of mean must be subtracted by the constant. The value of variance must be corrected too, but I don’t know how.
See the response that I just sent you to your previous comment.
Charles