Signed Ranks Exact Test

We now show how to calculate exact p-values and values for -crit without using the normal approximation. In fact, this approach is used to create the table of critical values (see Signed Rank Table). Technically, this approach is accurate for samples without ties, although the results will still be pretty accurate unless there are a lot of ties.

Example

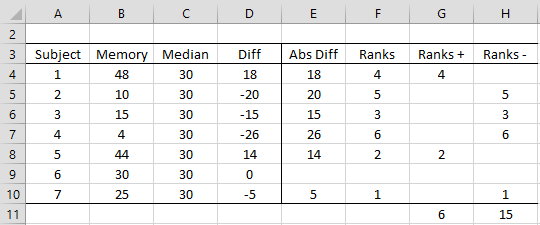
Example 1: Repeat the analysis for Example 3 of the Wilcoxon Signed Ranks Test using the data in Figure 1.

Figure 1 – Wilcoxon Signed Ranks Exact Test

Note that the ranks of the absolute values of the differences (column F) take the values 1, 2, 3, 4, 5, and 6 (with no repetitions since we are not allowing ties and we have eliminated the sample item that has 0 as its difference). We are interested in the distribution of T+, i.e. all possible values for the sums of the ranks for the positive entries.

All possible combinations

Figure 2 shows all possible combinations of ranks for positive and negative entries where 1’s correspond to positive entries and 0’s correspond to negative entries (range A5:BM12, displayed in two blocks so that they fit on the page). E.g. column U corresponds to the case where ranks 1, 3, and 4 are for positive entries, and ranks 2, 5, and 6 are for negative entries. Column AS corresponds to the situation in Example 1 (as shown in columns G and H of Figure 1).

Figure 2 – Distribution of ranks

The cells in row 12 contain the T+ values for the entries in that column. E.g. the sum of 8 in cell U12 is calculated by the formula =SUMPRODUCT($A6:$A11,U6:U11). These values range from 0 (column BM) to 1+2+3+4+5+6 = 21 (column B).

Note that 21 = (6·7)/2, or in general n(n+1)/2. We see that the value in AS12 is 6, which matches the value calculated in cell G11 of Figure 1. Note too that there are 2⁶ = 64 data columns in the table in Figure 2. In general, this value is 2ⁿ.

Permutation Distribution

The data in Figure 2 helps us calculate what we are really interested in, namely the distribution of all possible values of T+. This distribution, which we will call the (one-sample) permutation distribution, is shown in Figure 3.

Figure 3 – Distribution of T+

Since the possible values of T+ range from 0 to 21, we see there are 22 data entries in the table. The frequency of each of the T+ values is shown in row 15. E.g. the frequency value when T+ = 6 (i.e. cell H15) is calculated by the formula =COUNTIF($B12:$BM12,H14) and has a value of 4.

As we observed previously, the sum of all these frequencies (cell X15) is 64. The probabilities of any T+ value are shown in row 16 and the cumulative probabilities are shown in row 17. E.g. the probability that T+ has value 6 is 4/64 = .063 (cell H16) using the formula =H15/$X15. The cumulative probability is .219 (cell H17) using the formula =G17+H16.

Note too that the distribution shown in Figure 3 is symmetric around the value 21/2 = 10.5.

Analysis

Since p-value = .219 > .05 = α, we conclude (one-tailed test) that there is no significant difference between the population median and 30. This is also true of the two-tailed test since .219 > .025 = α/2 (or by symmetry, p-value = .438 > .05 = α).

We also note that the first value of T+ whose p-value ≥ .05 is T+ = 3. This means that for values of T+ ≤ 2 there is a significant difference between the population median and 30 based on a one-tail test with α =.05, or a two-tail test with α =.1. Note that for n = 6 and α = .1 the critical value for a two-tailed test shown in the Signed Ranks Table is T+ = 2.

For all values of T+ in the closed interval [3, 18] the null hypothesis is not rejected (with 90% confidence), while for values outside this range, the null hypothesis is rejected.

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack contains the following functions which calculate the exact p-value and critical value for the Wilcoxon signed-ranks test.

PERMDIST(x, n, cum) = value of the permutation distribution at x based on n elements; returns the pdf value at x if cum = FALSE and the cdf value if cum = TRUE

PERMINV(p, n) = inverse of the permutation distribution at  p; i.e. the least value of  x such that PERMDIST(x, n, TRUE) ≥ p

SRDIST(x, n, tails) = p-value of the signed-ranks exact distribution at x based a sample with on   elements where tails = 1 or 2 (default)

SRINV(p, n, tails) = inverse of the signed-ranks exact distribution at p; i.e. the least value of x such that SRDIST(x, n, tails) ≥ p where tails = 1 or 2 (default)

SR_EXACT(R1, R2, tails) = p-value of the paired signed-ranks exact test on the data in R1 and R2, where tails = 1 or 2 (default)

SR_EXACT(R1, med, tails) = p-value of the one sample signed-ranks exact test on the data in R1 and hypothetical median med (default 0), where tails = 1 or 2 (default)

Here n is the sample size less any elements that match the hypothetical median in the single sample case and less any sample pairs that are equal in the paired samples case.

Observations

Note that =SR_EXACT(R1, R2, 1) is equivalent to

=PERMDIST(SRANK(R1, R2), COUNTIF(R1,”<>”&R2))

and similarly for SR_EXACT(R1, med).

Also note that if x < n(n+1)/4, then

SRDIST(x, n, 1) = PERMDIST(x, n)

SRDIST(x, n, 2) = 2*PERMDIST(x, n)

while if x ≥ n(n+1)/4, then

SRDIST(x, n, 1) = 1–PERMDIST(x, n)

SRDIST(x, n, 2) = 2*(1–PERMDIST(x, n))

Also, if p ≤ .5, then

SRINV(p, n, 1) = PERMINV(p, n)

SRINV(p, n, 2) = PERMINV(p/2, n)

while if p > .5, then

SRINV(p, n, 1) = PERMINV(1–p, n)

SRINV(p, n, 2) = PERMINV((1–p)/2, n)

For the two-tailed test for Example 1, we have

SRDIST(6, 6, 2) = .4375

SRINV(.05, 6, 2) = 0

SR_EXACT(B4:B10, 30) = .4375

Speeding up the calculations

The approach described above for manually calculating the exact p-values is quite slow. Instead, we can use the following properties to recursively perform the calculations.

For samples of size n > 1, the sampling frequency of the T statistic f_n(T) has the following property:

for values of T between 0 and C(n+1, 2). Also, f₁(0) = f₁(1) = 1 and f_n(T) = 0 for all value of T < 0 or T > C(n+1, 2).

Example

Example 2: Calculate the frequency function f₅(T) for all possible values of T.

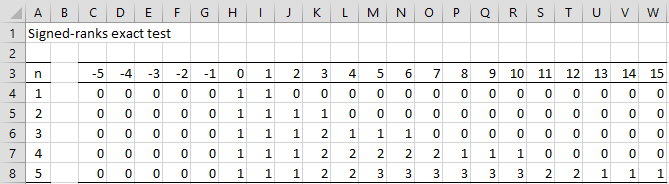
T takes values from 0 to C(5+1, 2) = 15. To calculate f₅(T) for these values of T, we first need to calculate the values of f_m(T) for all values of m = 1, 2, 3, 4, and for all values of T = -5, -4, …, 14, 15. This is shown in Figure 4.

Figure 4 – Signed-Ranks Exact Test

We start by filling in the value of zero for T < 0 (columns C through G). We next fill in the values for row 4, namely 1 for T = 0 or 1 and 0 elsewhere.

We now place the formula =H4+OFFSET(H4,0,-$A5) in cell H5, highlight the range H5:W8 and then press Ctrl-R and Ctrl-D.

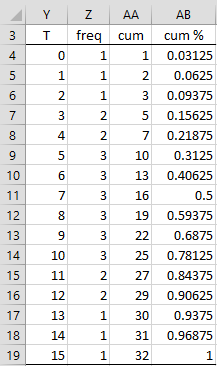
From row 8, we get the frequencies and cumulative distribution values for samples of size 5, as shown in Figure 5.

Figure 5 – Exact distribution

Columns Y and Z are the transposes of rows 3 and 8 from Figure 4. As usual, column AA is calculated by placing the formula =Z3+AA4 in cell AA4, highlighting the range AA4:AA19, and pressing Ctrl-D. Column AB is calculated by placing the formula =AA4/AA$19 in cell AB4, highlighting range AB4:AB19, and pressing Ctrl-D.

Note that the value of 32 in cell AA19 is 2⁵. In general, the denominator used to calculate the cumulative distribution value is 2ⁿ where n is the sample size.

Note that =PERMDIST(10,5) has the value .78125, as shown in cell AB14 of Figure 5. Also =SRDIST(4,5,2) has the value 2*.21875 = .43750.

Worksheet Array Function

Real Statistics Function: The Real Statistics Resource Pack contains the following array function that calculates the complete range of exact p-values for the specified sample size.

PERM_DIST(n, cum) returns a column array with the p-values of the Signed-Ranks exact test for values of T from 0 to C(n+1,2) when cum = TRUE (default) and the frequency values when cum = FALSE.

The formula =PERM_DIST(5) returns the array in range AB4:AB19 of Figure 5 and the formula =PERM_DIST(5,FALSE) returns the array in range Z4:Z19.

The functions PERMDIST, PERMINV, SRDIST, SRINV, SR_EXACT, and PERM_DIST work pretty well for values of n up to 500. You will be able to use larger sample sizes, but calculation times may become unacceptably long, or overflow errors may occur.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Wikipedia (2018) Wilcoxon signed-rank test
https://en.wikipedia.org/wiki/Wilcoxon_signed-rank_test