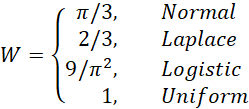To estimate the power of a signed ranks test for a sample (or the difference between pairs of elements in two samples) of size n calculate an adjusted sample size n* = n/W where W depends on the distribution of the sample as follows
and then conduct a one-sample t-test using the adjusted sample size n*.
The minimum sample size for a signed-ranks test is n*W where n* is the sample size for the one-sample t-test.
As described in Mann-Whitney Power we can use simulation to estimate the power of a one-sample or two-sample signed ranks test.
Worksheet Function
Real Statistics Function: The following function is provided in the Real Statistics Pack.
SR_POWER(effect, n, iter, dist, tails, ties, cont, alpha) = the power of a signed-ranks test on a sample from a distribution of type dist (default “norm”) of sizes with effect size effect based on iter simulations (default 100).
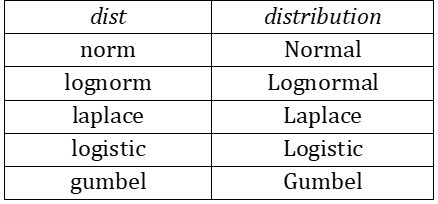
tails = # of tails = 1 or 2 (default). If ties = TRUE (default) a ties correction is applied. If cont = TRUE (default) a continuity correction is applied. alpha = the significance level (default .05). This function supports the distributions shown in Figure 1. The corresponding dist arguments are also shown in Figure 1.
Figure 1 – dist argument
Example
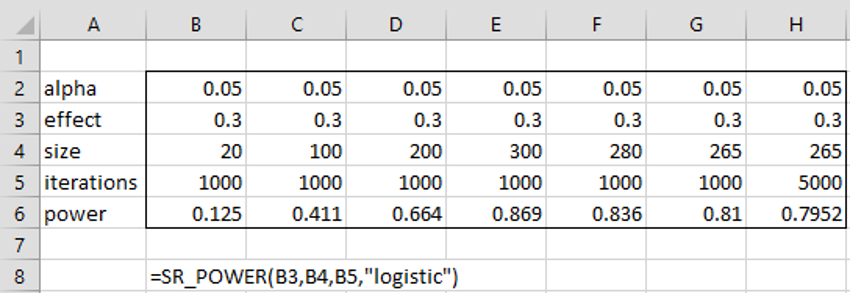
Example 1: Use simulation to determine the power of the signed-ranks test for a sample of size 20 from a logistic distribution with effect size .3. What sample size is required to achieve power of 80%?
We see from cell B6 of Figure 2 that the statistical power of the signed-ranks test is about 12.5% using the formula =SR_POWER(B3,B4,B5,”logistic”). If we increase the sample size progressively, we arrive at a power of approximately 80% when the sample size is about 265, as shown in cells H6 and I6.
Figure 2 – Power of a signed-ranks test
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Wikipedia (2018) Wilcoxon signed-rank test
https://en.wikipedia.org/wiki/Wilcoxon_signed-rank_test
Howell, D. C. (2010) Statistical methods for psychology (7th ed.). Wadsworth, Cengage Learning.
https://labs.la.utexas.edu/gilden/files/2016/05/Statistics-Text.pdf
NCSS PASS (2020) Wilcoxon signed-rank tests
https://www.ncss.com/wp-content/themes/ncss/pdf/Procedures/PASS/Wilcoxon_Signed-Rank_Tests.pdf