Property 1
Suppose sample 1 has size n1 and rank sum R1 and sample 2 has size n2 and rank sum R2, then R1 + R2 = n(n+1)/2 where n = n1 + n2.
Proof: This is simply a consequence of the fact that the sum of the first n positive integers is . This can be proven by induction. For n = 1, we see that
= 1 = n. Assume the result is true for n, then for n + 1 we have, 1 + 2 + … + n + (n+1) =
+ (n + 1) =
=
Property 2
When the two samples are sufficiently large (say of size > 10, although some say 20), then the W statistic is approximately normal N(μ, σ2) where
Proof: We prove that the mean and variance of W = R1 are as described above. The normal approximation was proven in Mann & Whitney (1947) (see reference at the end of this webpage) and we won’t repeat the proof here.
Let xi = the rank of the ith data element in the smaller sample. Thus, under the assumption of the null hypothesis, by Property 1
By Property 4a of Expectation
As we did in the proof of Property 1, we can show by induction on n that
![]()
From these, it follows that
We can now calculate the following expectations:
Also where i ≠ j
![]()
By Property 2 of Expectation (case where i = j)
By Property 3 of Basic Concepts of Correlation when i ≠ j
Using an extended version of Property 6 of Basic Concepts of Correlation we see that
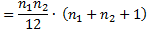 Reference
Reference
Mann, H. & Whitney (1947) On a test of whether one of two random variables is stochastically larger than the other. Annals of Mathematical Statistics, 18, p50-60.
http://projecteuclid.org/download/pdf_1/euclid.aoms/1177730491
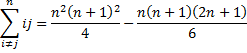
oh ,now i understand it!thanks your respond
It’s 2Σ i!=j to n1 [-(n+1)/12].I write wrong. There should’t ‘2’ in there i think .
Jack,
You need to sum all the terms cov(x_i,x_j) where i not equal to j. Note that each such covariance is repeated twice, once for cov(x_i,x_j) and once for cov(x_j,x_i). Thus, if you assume that the sum is where i < j, then you need to double the result. Another way to look at this is to determine how many pairs there are for the indices 1 to n1 where the indices are not equal. The answer is n1(n1-1), which is the value used in the proof. This is the same as 2 times n1(n-1)/2, the later being the number of pairs where the first index is less than the second index. To make this much clearer and more accurate, I have now replaced the lower limit of the summation symbol by i < j (instead of i not equal to j). Thanks for bringing this issue to my attention. Charles
Mr Charles, may be you not believe but it is true that until today I know you replay me with message. And my written english is not good.It is difficult to get in touch with world web.In 2017,after i ask you the question,the next day i found you have changed i!=j to i<y.But stupid web do not let me see you replay message.Watch your proof spend lot of time,especially 2Σ i!=j to n1 [-(n+1)/12]. now i see your message.but some words i don not get understand,I forget many details about proof. So I just want to know Σ i!=j to n1 [-(n+1)/12] is right ? And Σ i!=j to n1 [-(n+1)/12] is equal 2Σ i<j to n1 [-(n+1)/12] ?
Jack,
Sorry, but I don’t understand the notation:
Σ i!=j to n1 [-(n+1)/12] is right ? And Σ i!=j to n1 [-(n+1)/12] is equal 2Σ i
the last third lines. now you change “2Σ (i!=j to n1) [-(n+1)/12] ” to “2Σ (i<j to n1) [-(n+1)/12]" .I want to know if "Σ (i!=j to n1) [-(n+1)/12]" equals to "2Σ (i<j to n1) [-(n+1)/12] "
Jack,
I still don’t understand your notation. What does i! mean in the notation Σ (i!=j to n1) …
Charles
Sir
i!=j means i not equal to j
the last third lines. now you change “2Σ (i!=j to n1) [-(n+1)/12] ” to “2Σ (i<j to n1) [-(n+1)/12]" .I want to know if "Σ (i!=j to n1) [-(n+1)/12]" equals to "2Σ (i<j to n1) [-(n+1)/12] "
now i have a tweet account. So I send picture to you.
Jack,
Thanks for sending me the tweet. This makes everything clear.
The equation you wrote is correct (as long as i, j <= n1). Charles
Thank you !
I have one question about this proof. You calculate the expectation E(rirj) for all j not equal i. I don’t understand why we could take this expectation as equivalent to E(rirj) for all j, i. In the covariance we have to use E(rirj) of all rangs, but you use the expectation for all j not equal i, why is it correct? Can you explain me this problem?
Thanks for your answer!
Marcel,
I show E[ri rj] both where i = j (i.e. var(ri)) and where i is not equal to j.
Charles
I am grateful to you for your answer. But I wanted to say that you take the expectation E(rirj) with i not equal to j by the covariance cov(rirj). I don’t understand, why we can do this. I thought we need the expectation of all i and j (also of the double sum i*j).
I made a print-screen with both places in your proof: https://image.prntscr.com/image/7lBOfbg1RribBEjyIbN1Kw.png
Marcel,
Thanks for clarifying things. There are two case: (1) where i = j and (2) where i is not equal to j. In case (1) cov(rirj) = var(ri), which is the described in your print-screen. In case (2) the formula is the one shown in your print-screen. I have just updated the referenced webpage to try to make this a bit clearer. Does it help?
Charles
Thank you very much!
I understand it now.
Marcel,
Good to hear. Glad I could help.
Charles
Your site is very good!
Have you thougt about translate your work in other languages?
Marcel,
I hadn’t. What languages did you have in mind?
Charles
I think about German and Polish. I could help you .
Marcel,
Thanks for the offer, but so far people haven’t been asking for translations. In any case, I’ll think about it.
Charles
Thanks alot, you realy put it out on paper
I’m grateful for dis better understanding
Thanks. Good one
thanks 😀
thanx! really helpful!