Wilcoxon Rank Sum Exact Test

Basic Concepts

We now show how to calculate exact p-values and values for W-crit without using the normal approximation. In fact, this approach is used to create a table of critical values (Wilcoxon Rank Sum Table). Technically, this approach is accurate for samples without ties, although the results will still be pretty accurate unless there are a lot of ties.

In order to illustrate the concepts involved, we will use a very small data set, as shown in the next example.

Example

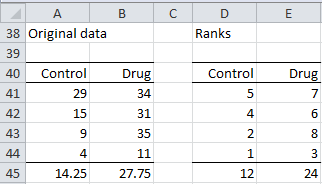
Example 1: Repeat Example 1 of Wilcoxon Rank Sum Test with the data shown in Figure 1 for a two-tailed test with α = .10.

Figure 1 – Wilcoxon Rank Sum Exact Test Data

Note that the ranks of the data (range D41:E44) take the values 1 through 8 (with no repetitions since we are not allowing ties). We are interested in the distribution of W, i.e. all possible values for the sums of the ranks.

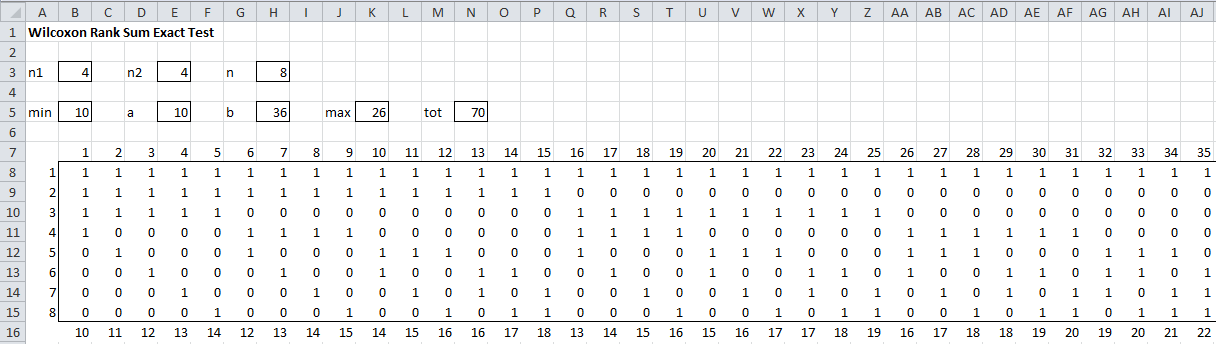
Figure 2 shows all possible combinations of ranks with four entries for Control (specified by 1’s) and four entries for Drug (specified by 0’s).

Figure 2 – Distribution of Ranks

Here n1 (cell B3) and n2 (cell E3) are the number of elements in the Control and Drug samples, with n1 ≥ n2 (note that if n1 < n2 we simply reverse the roles of Control and Drug) and n = n1 + n2 (cell H3). The sum 1 + 2 + … + n1 = the smallest value for the sum of the ranks for Control, which is n1(n1 +1)/2. For Example 1, n1 = 4, n2 = 4, n = 4+4 = 8 and the minimum sum of ranks for Control = 1 + 2 + 3 + 4 = 10, which is the same as n1(n1 +1)/2 = 4·5/2 =10.

Rank Sums

The range B8:BS15 contains all possible combinations of ranks distributed between Control and Drug. To fit on the page, this range is displayed in two blocks in Figure 2. E.g. column AZ contains the entry where Control contains four elements with ranks 2, 4, 7, and 8 (and so Drug contains the elements with ranks 1, 3, 5, and 6). The sum of the ranks for Control is therefore 2 + 4 + 7 + 8 = 21, which is shown in cell AZ16. Note that this value is calculated via the formula =SUMPRODUCT($A8:$A15,AZ8:AZ15). Note that column G corresponds to the ranks of the Control and Drug data for Example 1.

There are C(n, n2) = C(8,4) = 70 data entries. Now let b = 1 + 2 + … + n = n(n+1)/2 = 36 (cell H5) and a = 1 + 2 + … + n2 = n2(n2+1)/2 = 10 (cell E5). It follows that the maximum sum of ranks for Control is given by b – a = 36 – 10 = 26 (cell K5).

Permutation Distribution

The table in Figure 2 helps us calculate what we are really interested in, namely the distribution of all possible values of W. This distribution, which we will call the two-sample permutation distribution, is shown in Figure 3.

Figure 3 – Distribution of W

As we have seen, the possible values of W range from 10 to 26. The frequency of each of the possible W values is given in row 19. E.g. the frequency value for W = 16 (i.e. cell H19) is given by the worksheet formula =COUNTIF($B16:$BS16,H18) which has a value of 7.

The sum of all these frequencies (cell S19) is 70, as we saw previously. The probabilities of any possible W value are given in row 20 and the cumulative probabilities are given in row 21. E.g. the probability that W has value 16 is given by 7/70 = .1 (cell H20) using the formula =H19/$S19. The cumulative probability is .343 (cell H21) using the formula =G21+H20.

Note too that the distribution shown in Figure 3 is symmetric around the value (26-10)/2 = 18.

Test Results

Since for Example 1, W = 12, we see that p-value = .057 (cell D21 in Figure 3). Since p-value = .057 < .10 = α, we conclude (one-tailed test), there is a significant difference between the medians of Control and Drug populations. For a two-tailed test, .057 > .05 = α/2 (or by symmetry, p-value = .114 > .1 = α), and so we would conclude there is no significant difference between the medians of Control and Drug populations.

We also note that the first value of W whose p-value ≥ .05 is W = 12. This means that for values of W < 12, there is a significant difference between the population medians for Control and Drug based on a one-tail test with α =.05, or a two-tail test with α =.10. Note that for n1 = 4, n2 = 4 and α =.10 the critical value for a two-tailed test shown in the Wilcoxon Rank Sum Table is W = 11.

For all values of W in the interval [12, 24] the null hypothesis is not rejected (with 90% confidence), while for values outside this range, the null hypothesis is rejected.

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack contains the following functions that implement the process described above.

PERM2DIST(x, n1, n2, cum, FALSE) = value of the two-sample permutation distribution at x based on n1 and n2 elements; returns the pdf value at x if cum = FALSE and the cdf value if cum = TRUE (default)

PERM2INV(p, n1, n2, FALSE) = inverse of the two-sample permutation distribution at p; i.e. the least value of  x such that PERM2DIST(x, n1, n2, TRUE, FALSE) ≥ p

Note that there are two versions of the two-sample permutation distribution. The version illustrated here is used for the Wilcoxon rank-sum test, while another version is used with the Mann-Whitney test (see Mann-Whitney Exact Test). If the fourth argument of the PERM2DIST and PERM2INV functions is FALSE, then the Wilcoxon rank-sum version is used, while if the fourth argument is TRUE (the default), then the Mann-Whitney version is used.

Observations

The p-value of Wilcoxon’s Rank-Sum one-tail test for test statistic W and sample sizes n1 and n2 is given by the formula PERM2DIST(MIN(W, W’), n1, n2, TRUE, FALSE). The critical value for any value of alpha is PERM2INV(α, n1, n2, FALSE). The two-tail test is given by 2*PERM2DIST(x, n1, n2, TRUE, FALSE) and PERM2INV(α/2, n1, n2, FALSE).

Thus for the two-tailed test for Example 1, we have

p-value = 2 * PERM2DIST(MIN(W, W’), n1, n2, TRUE, FALSE)
= 2 * PERM2DIST(105.5, 12, 11, TRUE, FALSE) = .104

W-crit = PERM2INV(α/2, n1, n2, FALSE) = PERM2INV(.05/2, 12, 11, FALSE) = 99

Large samples

For very large samples, the PERM2DIST and PERM2INV worksheet functions can become computationally intensive. You shouldn’t have too much of a problem if the smaller of n1 and n2 is at most 300 while the larger is at most 1,000. You will be able to use larger sample sizes, but calculation times may become unacceptably long, or overflow errors may occur (in which case PERM2DIST may even produce a negative value).

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Wild, C. (1997) The Wilcoxon Rank-Sum test
https://www.stat.auckland.ac.nz/~wild/ChanceEnc/Ch10.wilcoxon.pdf

Marx et al. (2016) Exact dynamic programing solution of the Wilcoxon–Mann–Whitney test
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4792850/