Basic Concepts
When the requirements of the t-test for two independent samples are not satisfied, the Wilcoxon Rank-Sum non-parametric test can often be used provided the two independent samples are drawn from populations with an ordinal distribution.
For this test, we use the following null hypothesis:
H0: the observations come from populations with the same distribution
From a practical point of view, this implies:
H0: if one observation is made at random from each population (call these observations x0 and y0), then the probability that x0 > y0 is the same as the probability that x0 < y0
For example, the Wilcoxon Rank-Sum test can be used to determine whether there is a significant difference in the effectiveness of two treatments (this being the alternative hypothesis).
Hypothesis about the median
If we make the further assumption that the two population distributions have the same shape (justified by using histograms or box plots), then the null hypothesis can be viewed as taking the form:
H0: the samples come from populations with the same median
This assumption is not satisfied, for example, if one sample is highly skewed to the left and the other is skewed to the right.
Typically, the Wilcoxon Rank-Sum test is used when the data in one or both samples are not normally distributed. Keep in mind, however, that the two-sample t-test is pretty robust to violations of normality and so a non-parametric test is only needed when the normality assumption is strongly violated (e.g. the data is heavily skewed), especially when there is the presence of outliers.
Example using table of critical values
Example 1: Repeat Example 2 from Two Sample t Test with Unequal Variances to determine whether a new hay fever drug is effective, but this time using the data from Figure 1.
Figure 1 – Data for Example 1
Testing the Assumptions
When we look at the QQ Plot for the Control group we see that the data are not very normally distributed. More concerning is that the Box Plot for the group that took the drug shows that the data are not very symmetric (see Figure 2). We, therefore, decide to use the Wilcoxon Sign-Rank test instead of the t-test.
Figure 2 – QQ Plot and Box Plots for data in Example 1
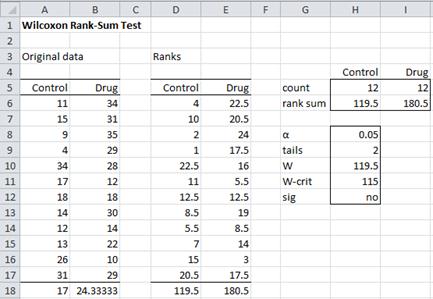
The results of the Wilcoxon Rank-Sum test are displayed in Figure 3.
Figure 3 – Wilcoxon Rank-Sum Test for Example 1
Calculating Ranks
We begin by calculating the ranks of the combined 24 raw scores using the RANK.AVG worksheet function (or Real Statistics’ RANK_AVG function for users of Excel prior to 2010). See Ranking for details. For example, cell D6 in Figure 3 contains the rank of the first participant in the Control group, as calculated by the worksheet formula RANK_AVG(A6,$A$6:$B$17,1) which is the same as
=RANK(A6,$A$6:$B$17,1) + (COUNTIF($A$6:$B$17,A6)-1)/2.
using the standard Excel 2007 rank function (see Ranking).
We then calculate the sum of the ranks for each group to arrive at the rank sums R1 = 119.5 and R2 = 180.5. Since the sample sizes are equal, the value of the test statistic W = the smaller of R1 and R2, which for this example means that W = 119.5 (cell H10).
Test Results
We next compare W with the critical value Wcrit, which can be found in the Wilcoxon Rank-Sum Table. Since the sample sizes are both 12, we look up the critical value in the table for α = .05 (two-tail) where n1 = n2 = 12, and find that Wcrit = 115. This represents the smallest value we could expect to obtain for W if the null hypothesis were true. Since W = 119.5 ≥ 115 = Wcrit, we cannot reject the null hypothesis, and so conclude there is no significant difference between the effectiveness of the drug and the control.
Example with unequal sample sizes
Example 2: Repeat Example 1 with the last data element in the Drug group removed.
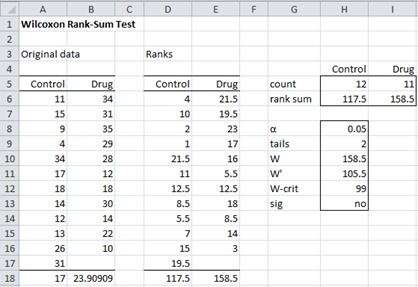
We again use the Wilcoxon Rank-Sum test, but this time the sample sizes are unequal. The test is shown in Figure 4.
Figure 4 – Wilcoxon Rank-Sum Test for Example 2
The rank sums are calculated as in the previous example, although since some of the data may be blank, we need to use a formula such as
=IF(A6<>””,RANK_AVG(A6,$A$6:$B$17,1),””)
Also, since the Drug sample is smaller than the Control sample, we need to set W to be the rank sum of the smaller sample, namely 158.5 (cell I6).
Caution
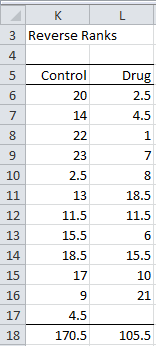
Also, because the sample sizes are different, a bit more care is required. Essentially W represents the left tail statistic and so we need to also evaluate the right tail statistic W′, which can be obtained by using reverse ranking shown in Figure 5:
Figure 5 – Calculation of W′ using reverse ranks
The value of W′ is, therefore, the sum of the ranks for the smaller sample, i.e. 105.5. Note that this is not the value in cell H6. Fortunately, because of symmetry, W′ can be calculated more easily via the formula
W′ = n1(n1 + n2 +1) – W
where n1 = 11 (the smaller sample size) and n2 = 12 (the larger sample size). Thus we obtain
W′ = 11(11+12+1) –158.5 = 105.5 (the value shown in cell H11)
For the two-tailed test, which is what we usually require, we compare the smaller of W and W′ with Wcrit. To find the value of Wcrit, we again use the Wilcoxon Rank-Sum Table with α = .05 (two-tailed test) where n1 = 11 and n2 = 12 to obtain Wcrit = 99. Since min(W, W′) = min(158.5, 105.5) = 105.5 ≥ 99 = Wcrit , once again we cannot reject the null hypothesis.
Observation: When n1 = n2, then W′ = max(R1, R2), i.e. the larger rank sum. Thus in Example 1, W′ = 180.5, although we don’t need to explicitly calculate its value.
Properties
Property 1: Suppose sample 1 has size n1 and rank sum R1 and sample 2 has size n2 and rank sum R2, then R1 + R2 = n(n+1)/2 where n = n1 + n2.
Property 2: When the two samples are sufficiently large (say of size > 10, although some say 20), then the W statistic is approximately normal N(μ, σ2) where
Click here for a proof of Property 1 or 2.
Observations
Using Property 2, for samples sufficiently large, we can test W using the techniques from Sampling Distributions. Note that the result is the same whether we use W or W′.
Since it compares rank sums, the Wilcoxon Rank-Sum test is more robust than the t-test as it is less likely to obtain spurious results based on the presence of outliers. Even for large samples where the assumptions for the t-test are met, the Wilcoxon Rank-Sum test is only a little less efficient than the t-test.
Example using the normal approximation
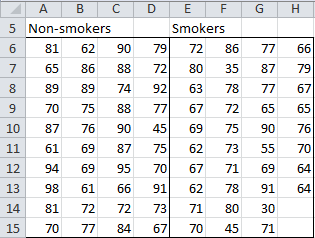
Example 3: The objective of a study was to determine whether there is a significant difference in the median life expectancy between smokers and non-smokers. 38 smokers and 40 non-smokers were chosen at random and their age at death was recorded as shown in Figure 6.
Figure 6 – Life expectancy for both groups
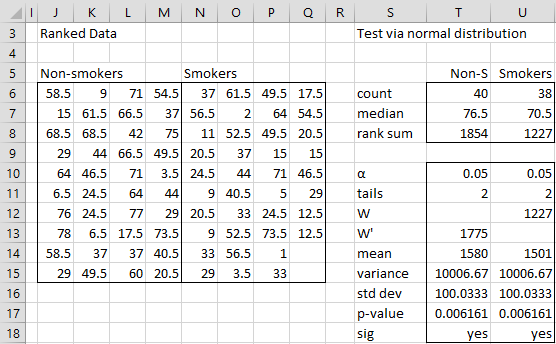
A table of ranks was created and the values of W and W′ were calculated as in Examples 1 and 2. Since the sample sizes are sufficiently large, we can test W (or W′) using the normal distribution as described in Figure 7.
Figure 7 – Wilcoxon rank-sum test using normal approximation
Since there are fewer smokers than non-smokers, W = the rank sum for the smokers = 1227 (cell U8). We calculate the mean (cell U14) and variance (cell U15) for W using the formulas =U6*(T6+U6+1)/2 and =U14*T6/6 respectively. The standard deviation (cell U16) is then given by the formula =SQRT(U15) as usual.
Calculating the p-value
We now calculate the p-value (cell U17) using the formula =2*NORM.DIST(U8, U14, U16, TRUE) since W < W̄. If W > W̄, we would use the formula =2*(1 – NORM.DIST(U8, U14, U16, TRUE)). Alternatively, we could have created the z-score and calculated the p-value using NORM.S.DIST.
Since p-value = .006161 < .05 = α, we reject the null hypothesis (two-tailed test) and conclude that there is a significant difference between the life expectancy of smokers and non-smokers.
Note that had we used W′ (column T of Figure 7), we would get the same p-value and come to the same conclusion.
Continuity Correction
Some apply what is called a continuity correction to the value of W. The assumption is that a value of W = 1227 (such as in Example 3) really represents a continuous interval (1226.5, 1227.5), and so instead of using the value W = 1227, they use the value W = 1227.5 (i.e. the endpoint of the interval closer to the mean value) when employing the normal approximation.
Worksheet Functions
Real Statistics Functions: The following functions are provided in the Real Statistics Pack:
RANK_COMBINED(x, R1, R2, d) = the ranking of element x among all the elements in R1 and R2 combined.
RANK_SUM(R1, R2, d) = the sum of the ranks of all the elements in R1 based on the ranking of all the elements in R1 and R2 combined.
RANK_SUM(R1, k, d) = sum of the ranks of all the elements in the kth column of R1.
If d = 0 (or is omitted), then the rankings are in decreasing order; otherwise, they are in increasing order. Rankings are corrected for ties as in RANK.AVG or RANK_AVG (see Ranking). Any empty or non-numeric cells in R1 or R2 are ignored.
WILCOXON(R1, R2) = minimum of W and W′ for the samples contained in R1 and R2
WILCOXON(R1, k) = minimum of W and W′ for the sample contained in the first k columns of R1 and the sample consisting of the remaining columns of R1. If the second argument is omitted it defaults to 1.
WTEST(R1, R2, tails) = p-value of the Wilcoxon rank-sum test for the samples contained in R1 and R2 by using the normal approximation; tails = the # of tails: 1 (default) or 2.
WTEST(R1, k, tails) = p-value of the Wilcoxon rank-sum test for the sample contained in the first k columns of R1 and the sample consisting of the remaining columns of R1. If the second argument is omitted it defaults to 1. tails = the # of tails: 1 (default) or 2.
WCRIT(n1, n2, α, tails, interp) = critical value of the Wilcoxon Rank-Sum test for samples of size n1 and n2 for the given value of alpha (default α = .05) and tails = 1 (one tail) or 2 (two tails, default) based on the Wilcoxon Rank-Sum Table.
WPROB(x, n1, n2, tails, iter, interp) = an approximate p-value for Wilcoxon rank-sum test x (= the minimum of W and W′) for samples of size n1 and n2 and tails = 1 (one tail) or 2 (two tails, default) based on the values in the Wilcoxon Rank-Sum Table using iter number of iterations (default = 40).
If interp = TRUE (default) then the recommended interpolation is used if necessary in the table lookup; otherwise, linear interpolation is used.
Note that the values for α in Wilcoxon Rank Sum Table range from .01 to .2 for tails = 2 and .005 to .1 for tails = 1. If the p-value is less than .01 (tails = 2) or .005 (tails = 1) then the p-value is given as 0 and if the p-value is greater than .2 (tails = 2) or .1 (tails = 1) then the p-value is given as 1.
Any empty or non-numeric elements in R1 or R2 are ignored.
Observations
If R1 represents the first k columns of R and R2 represents the remaining columns in R, then WILCOXON(R, k) = WILCOXON(R1, R2) and WTEST(R, k) = WTEST(R1, R2). Of course, WILCOXON(R1, R2) and WTEST(R1, R2) can also be used when R1 and R2 are two ranges that are not contiguous.
Similarly, if R1 represents the first k columns of R and R2 represents the remaining columns in R, then RANK_COMBINED(x, R1, R2, d) = RANK_AVG(x, R, d). The RANK_COMBINED function is especially useful, however, when R1 and R2 are two non-contiguous ranges.
Applying Worksheet Functions
In Example 2, WILCOXON(A6:B17) = 105.5, i.e. the minimum of W and W′. Also, RANK_COMBINED(34, A6:A17, B6:B7, 1) = 21.5, RANK_SUM(A6:A17, B6:B17) = 170.5 and RANK_SUM(B6:B17, A6:A17) = 105.5.
In addition, WCRIT(H5,I5,H8,H9) = WCRIT(12, 11, .05, 2) = 99 (the value in cell H12 of Figure 4). Finally note that the p-value = WPROB(H11,I5,H5,H9) = WPROB(105.5, 11, 12, 2) = .125 > .05 = α, and so once again we can’t reject the null hypothesis.
Similarly in Example 3, we can use the WILCOXON function to arrive at the same value for the minimum of W and W′, namely WILCOXON(A6:H15, 4) = WILCOXON(A6:D15, E6:H15) = 1227, as well as the same p-value (assuming a normal approximation), namely WTEST(A6:H15, 4) = WTEST(A6:D15, E6:H15) = 0.003081. Also RANK_COMBINED(72, A6:D15,E6:H15,1) = 37, RANK_SUM(A6:D15,E6:H15,1) = 1854 and RANK_SUM(E6:H15, A6:D15,1) = 1227.
Effect Size
The effect size for the Wilcoxon Rank Sum test can be expressed by the correlation coefficient (see Basic Concepts of Correlation). The correlation coefficient for the Wilcoxon Rank Sum test is given by the formula
where the z-score is
For Example 3,
and so
As described in Correlation in Relation to t-test, a rough estimate of effect size is that r = .5 represents a large effect size, r = .3 represents a medium effect size and r = .1 represents a small effect. Thus, for Example 3 we have a medium-sized effect.
Also, see Mann-Whitney Test (including Figure 2) for more information about how to calculate the effect size r in Excel.
Exact Test
Click here for a description of the exact version of the Wilcoxon Rank-Sum Exact Test using the permutation function.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Wild, C. (1997) The Wilcoxon Rank-Sum test
https://www.stat.auckland.ac.nz/~wild/ChanceEnc/Ch10.wilcoxon.pdf
Hollander, M., Wolfe, D. A. (1999) Nonparametric statistical methods, 2nd ed. Wiley
Charles,
I hope all is well!
I am using SPSS to perform the Wilcoxon Signed Rank (WSR) test to see if there is a significant difference (or not) between related paired exams scores (Exam 1 and Exam2). N = 225 . Both sets are not normally distributed (verified by Shapiro Wilks test).
I used SPSS to run the WSR test and I understand how to interpret the output.
However, I came across a WSR test assumption that I skipped. That is, that the distribution shape of the difference between the paired related values from the two has to be normal.
For example, find the difference between pair 1, pair 2, pair 3…all the way to pair 225. Make a list of the differences and see if that list is symmetric!
Should I have checked the paired differences data set to see if that distribution is normal before running the WSR? If the set is not normal, what do I do?
Also, I understand that being that the sample size is large, a normal approximation is used by SPSS to analyze the data for the WSR. Should I not worry about the first concern I mentioned.
HELP.
Thanks!
I just came across an old textbook and it doesn’t list that assumption. I am not sure where to do from here! I would appreciste your help.
Hello Virginia,
For a paired t-test you need to check whether the differences are normally distributed. You don’t need to check each sample for normality, just the differences. This is an assumption for the paired t-test. If the normality assumption is not met, then typically a paired WSR test is a good substitute for the paired t-test.
Charles
Cuál es el valor de n para identificar en la Tabla el estadístico de prueba de Wilcoxon, para n= 10 diferencias de dos filas de datos, de los cuales solo 6 de ellos quedan ordenados por rangos de los pruebas una suma de rangos? (es decir que los otros quedaron iguales; para p=0.05, unilátero, es T=11 para n=10?, o T=2 para n=6? )
Francisco,
For the Wilcoxon Rank Sum test, there are two samples and so there are two sample sizes n1 and n2. They don’t have to be equal.
Charles
Hello Charles,
I downloaded the real stats add-in and cannot find the WCRIT function you mentioned. Did it get removed?
Dillon,
It is still available even though you don’t see it as you enter the function in a spreadsheet.
The reason for this is that it has been replaced by the function MWINV(alpha, n1, n2, tails, False). This function gives an exact value instead of using a table lookup.
Charles
Charles – your website and statistical package are terrific! I’ve been searching through my old college statistics book and tons of other websites, and it’s hands down the best source. Thanks so much for this!
On the Wilcoxon Rank-Sum Test (one-tailed), I realize it’s normally used for determining if there’s a statistical difference between two groups, but is it possible to explicitly say one group is greater than or less than the other? The way the “final” W can be (1) the smaller of the two W’s (if same sample sizes) or (2) the W for the smaller sample size has me second-guessing if that’s possible. For an appropriately small W, you can say the groups are different, but is there a way to “force” the W to be for one group, so you can explicitly say which one is less than the other (perhaps depending on the sign of the Z-score)? I’m hoping to do that when running multiple comparisons and just having a simple “Group 1 Group”, or “Not Significantly Different” output.
Potentially related to that, on your Excel file example (Real-Statistics-Examples-Non-Parametric-1) on tab “Wilcoxon 4”, if you switch the “Smokers” and “Non-Smokers” data, the p-value rises from 0.006 to 1.99, but with the same Z-scores. Should that not keep the same p-value that would reject the hypothesis/could there be additional criteria on the “final” W that would correct for that? And further related to that, should that tab have a similar formula for when the sample sizes are the same to use the smaller W?
Thanks again!
Thanks for the kind words about the website.
1. W is the rank sum for the larger sample and W’ is the rank sum for the smaller sample. If there is a significant result, you can assign an order to the two groups based on the rank-sum divided by the sample size. If the two samples have similar shape (i.e it appears that they come from populations with the same type of distribution, then the sample with the smaller rank-sum divided by sample size would come from the population with the smaller median.
2. The p-value can’t be larger than 1 (it is a probability) and so p-value can’t be equal to 1.99. Even if you reverse the roles of smokers and non-smokers the p-value should be the same, namely .006.
Charles
I think I’ve confused myself with my first post, sorry!
In tabs “Wilcoxon 3” and “Wil Exact” of the “Non-Parametric 1” file, W is calculated as “the minimum rank sum” if the sample sizes are equal and as “the rank sum of the smaller sample” if the sample sizes are different (cell H10 in both). In the case of the different sample sizes, the W (and resulting W’) could come from either of the samples, and the output would only tell you they’re significantly different or not (you lose knowing which sample is which thru the IF statement). I was hoping for a way to output which sample is the lesser or greater of the two (in a one-tailed test).
Potentially related to that on tab “Wilcoxon 4,” when you switch the data between Non-smokers and Smokers, the W calculation changes from Smokers to Non-smokers (because sample sizes change), and that flows thru to make the p-value=1.99 currently. It seems like the p-value might need an IF statement to adjust to the other sample size (but that maybe the current layout would provide a way to “remember” the W, to potentially output which sample is lesser or greater than the other (instead of just different) like I was hoping above).
I’m probably too far in the weeds with my lack of knowledge, but thanks again for your help!
I think I understand your response #1 above now: After you’ve gotten a significantly different result, you can then divide the rank-sums (not the W or W’) by respective sample sizes, and the sample with the smaller of those would be significantly smaller (or similarly, the larger one would be significantly larger)?
So in Example 2/tab “Wilcoxon 3” (assuming a higher significance level that made them different), you could divide the the rank-sums of 117.5 and 158.5 by 12 and 11, to get 9.8 and 14.4, showing the first sample is smaller than the second. And in Example 3/tab “Wilcoxon 4,” you could divide 1854 and 1227 by 40 and 38, to get 46.4 and 32.3, showing the second sample is smaller than the first?
Thanks again!
I believe that what you said is correct. You can probably get the same result by using W, W’ and the sample sizes but I have not looked into this.
Charles
See my response to your later comment.
Charles
Charles,
For example 3, I would think that we will need to use the WTEST function with 2-tailed test. However, the p-value obtained using the 2-tailed function WTEST(R1, R2, 2) gave a 2 times bigger p-value than the p-value obtained using the normal approximation. Why?
In your observation paragraph, you have used 1-tailed WTEST function (ie, WTEST(A6:D15, E6:H15) = 0.003081.), which matches the p-value based on the normal approximation.
Hello Sun,
Thanks for pointing out this error. Since we are conducting a 2-tailed test, the p-value = 0.006161 (twice the value indicated). I have now corrected the webpage. You have been extremely helpful in identifying quite a few errors, for which I am very grateful.
Charles
Charles,
You are very welcome. There is one more area to be corrected in the body of the text shown below – please change “one tail test” to “two tail test”:
“Since p-value = .006161 < .05 = α, we reject the null hypothesis (one tail test) and conclude that there is a significant difference between the life expectancy of smokers and non-smokers."
Hi Sun,
Thanks again. I have just changed the text to “two tailed test” as you suggested.
Charles
Charles,
Please disregard my Q about WTEST(R1, R2). I did not realize that I should have typed tails=2 for 2-tailed test for this function. After adding the tails specification, I have the correct p-value.
My apology!
-Sun
Charles,
As I was not able to send the entire Qs of my original Qs, I divided up my Qs.
Here is the second one. It is about the p-value obtained based on WPROB.
For the WPROB formula, the first and second examples came back with bigger than the value of 1, which cannot be correct. And the 3rd example came back with an invalid value mark.
I used the smallest (or smaller) rank-sum W value followed by the smaller sample size, the other sample size, and 2 for 2-sided test.
For example, for the first example “=WPROB(119.5,12,12,2)”.
It came back with the value of 1.999….
I do appreciate your guidance on how to correct this.
-Sun
Charles,
I came across a few contradictory values in producing p-values using WTEST and WPROB.
For the first example, based on the W and the critical value, it was decided that the null hypothesis is not going to be rejected. When I used WTEST(R1,R2), it gives a p-value of 0.03912, instead of something bigger than 0.05. I downloaded your examples to check whether you have provided the p-value calculation. In your example, it seems that p-value is obtained using different formula 2*PERM2DIST. And this p-value seems to be the twice size of what I obtained from WTEST.
Please advise me how I can correct the error.
Thanks,
-Sun
Thank you Charles! I certainly appreciate your help with my queries. When I perform the function, the result I am getting is #NAME? Did I go wrong in installing the software?
What do you see when you enter =VER() into any cell?
Charles
It is returning the reusult #NAME?
Sunitha,
This means that you have not installed the Real Statistics software. You need to go back to the webpage from where you downloaded the software and follow the Installation instructions.
Charles
Thank you Charles, I could install Real Statistics software after a little bit of troubleshooting on my device. When I click =VER() it returns ‘5.6 Excel 2013/2016’ But when I close the excel file, I am having to choose adding the resource pack every time. Else =VER() is returning #NAME?
Is there anything else I need to do to install it correctly?
Sunitha,
I have not seen this problem before and don’t know what could cause it.
Which language are you using?
Charles
Hi Charles,
I uninstalled the software and installed it again and it is working fine now.
Thank you for all the help with the installation.
Regards,
Sunitha.
Hi Charles,
Thank you for putting together this wonderful website!
I have a quick query. For the wilcoxon test, can I have n1=9 and n2=27?
Thank you very much.
Sunitha,
Glad you like the website.
The Wilcoxon Rank Sum table in the website goes up to 25 x 25, and so doesn’t contain 9 x 27, but when I extrapolate 9 x 27 appears to be about 113 when alpha = .05. I doubt the real value is much different than 113 (perhaps 112 or 114).
Since the Wilcoxon Rank Sum can be calculated from the Mann-Whitney statistic, you could also use the MCRIT function which does support samples sizes up to 20 x 40 (but you need to make the proper adjustments).
Charles
Thank you so much Charles for a quick reply. Can you please explain what you mean by “but you need to make the proper adjustments”. I am researcher in the field of language sciences and have clue whatsoever of statistics at this depth.
Sunitha,
Sorry that I gave you such a cryptic response. It is actually quite straightforward. If you have the critical value from the Mann-Whitney table you just need to add m(m+1)/2 where m = the smaller of the sample sizes to get the corresponding value in the Wilcoxon Rank Sum table. For your situation the Real Statistics formula =MCRIT(9,27,.05) yields the Mann-Whitney critical value of 67. You need to add 9(9+1)/2 = 45 to this to get the Rank Sum critical value of 67+45 = 112.
Charles
Thank you Charles. I do not see the Real Statistics function MCRIT. I have downloaded and added the Real Statistics in excel add ins. Also, I have another query: Can I have the pretest and post values for the experimental and the control groups and still conduct a Wilcoxon Rank sum test?
This is not a data analysis tool. You need to simply type the formula =MCRIT(9,27,.05) in any cell. Wilcoxon Rank Sum only works for independent samples. For paired samples, you can use Wilcoxon’s Signed Ranks Test.
Pls when you have negative observations in Wilcoxon rank sum test, how do you go about the ranking.
Something like this (2,0,-1,5,6,1) .
Francis,
The ranking is done in the same way< the fact that there are negative observations doesn't change anything. (2,0,-1,5,6,1) has ranks (4,2,1,5,6,3) if lowest value is ranked 1 or (3,5,6,2,1,4) if highest value is ranked 1. Charles
Hi, when would you rank the highest value as 1, and rank the lowest value as 1? Is it when we have unequal sample size?
Also for a right tail test, what is the test statistics to be used?
Thanks !
Hello Richard,
Yes, this issue only arises when the sample sizes are unequal. I suggest that you always use the ranking where the lowest rank is 1 and then calculate W’ as described on this webpage. Better yet, use the Mann-Whitney test which is equivalent to the Wilcozon Signed Ranks Test but avoids this issue.
Charles
Dear Charles,
Thanks for introducing this new test.
In practice, I have one job which requires me to test if there is a drift for runs wkN vs wkN-1. i use t-test. But noticed there are cases whereby the runs are less than 30, and on top of that, the population is not normal distributed. In this case, can I say Wilcoxon Rank Sum Test will be more appropriate?
If yes, we 1st use QQ plot to validate that two samples from past 2 wks are not normal if they are not sitted close to the 45 degree line randomly. 2nd, we construct the WRS Tets and compare the W value with Wcritical to conclude whether or not there is a drift(two tail since we do not care the direction)?
Is my understanding and steps to make conclusion correct?
HJ,
You can still use the t test even when the population is not normally distributed provided the data is not too far from normally, especially if the data is reasonably symmetric.
You should also make sure that the two samples are independent. If not then instead of using the Wilcoxon Rank Sum test (or the Mann-Whitney test, which is equivalent), you should use the Wilcoxon Signed-Ranks test.
Provided you have two independent sample, then what you have stated seems correct.
Charles
Thank you for your exellent website. For a short comment, is it right to use the Wilcoxon Rank Sum test instead of Sign-Rank test shown in the below sentence in the text?
“We therefore decide to use the Wilcoxon Sign-Rank test instead of the t-test.”
KyleKim,
The Wicoxon Rank Sum test (or equivalently the Mann-Whitney test) and be used instead of the two independent sample t test, while the Wicoxon Signed Ranks test is used in place of the paired t test.
Charles
hi Charles thanks for clear explanation of the stage. my qoustion is how to inter those data on SPSS softwares?
Tariku,
Sorry, but I don’t use SPSS.
Charles
Hello,
first of all thanks for this very clear explanation!
I do have a “practical” question: I am trying to test big sample sizes, n1=40 and n2=29 and I cannot manage to find a table that gives me the critical values for n>20…. how can I find my critical W for a=0.05 to compare to my W left and W’ right?
Thanks a lot
Kind regards
Lara,
The largeest table I have seen only go up to n1 = 40 and n2 = 20, but with samples so large you can safely use the normal approximation instead of the tables of critical values. This approach is described on the referenced webpage.
Charles
hi! Charles do you about WILCOXON MANN-WHITNEY TEST ? and to get the U-statistics?
Jesmae,
See the following webpage:
Mann-Whitney Test
Charles
Hi Charles:
I have a question for example 2 (unequal samples).
n1=12; R1=117,5; R1’=170,5
n2=11; R2=158,5; R2’=105,5
Ws=min(158,5;105,5)=105,5
I don’t know if 158,5 is choosen because is the bigger value of left tail or because if the value of the smaller sample and no matter if is the bigger value or not.
Best regard
Felix
Felix,
The smaller sample is chosen.
Charles
May I use a Wilcoxon singed-rank test when the vairances are not similar between the two groups compared?
Thanks for your help
Alberto,
The Wilcoxon Signed Ranks test operates on the differences between the data items and so the variances won’t matter. The situation is different for the Wilcoxon Rank Sum test.
Charles
hi
I have a question in order to modify data by using wilcoxon rank-sum non-parametric rank. suppose I have a rating for 1 parameters which I have nitrate concentrates as well. I am going to modify rating respect to nitrate concentration. How would I be able to modify rating by Wilcoxon test?
for example:
rate nitrate concentration modified rate
4 1.3 ?
5 2 ?
8 18.5 ?
Sorry, but I don’t know what you mean by “modify data using wilcocon rank-sum non-parametric rank”.
Charles
Dear Sir,
I am using Wilcoxon rank sum test for my research results. I have results of two algorithms for 30 functions that means n1 is 30 and n2 is also 30. I calculated p value and used significant level .05. Now, I want to find which values of n1 (out of 30) is significantly different from n2. If the any of the value is significantly different then which one is better.
Thank you in anticipation.
Parul,
Sorry, but I don’t understand your question.
Charles
Hello, I am searching for the significance levels of a Wilcoxon rank sum (Mann-Whitney) test. I used stata to generate the p values but i am wondering at which level do i say the figures are significant at e.g 0.01, 0.05 0r 0.20? Is there a way i could select the level of significance in stata?
Peter,
The significance level really depends on you. It simply states the level of Type I error you are willing to accept for the test. The typical value is .05 (i.e. one type I error every 20 tests). You can set it lower if you like. See Null and Alternative Hypothesis for details.
Charles
Kindly help with this, its very urgent. What study design can be used for sign test, wilcoxon sign-ranked test, median test and mann whitney test. Thanks in anticipation.
Please look at the webpages for each of these tests to get the information that you are looking for.
Charles
Dear Dr. Charles,
I have two methods. Each method is tested on 8 samples and for each sample we have Precision, Recall, F-score. The method X has higher average F-score than method Y. However, the difference is small. I am asked to calculate the p-value of the difference.
Is the Wilcoxon rank sum test the correct way, or I should think in another direction?
How to calculate the p-value of the difference? Should I list the array F-score for X and array F-score for Y in Matlab and use the command ranksum?
Please advice.
Thanks a lot
My N1 is only 16, but N2 is 5035. How am I suppose to find alpha then?
Bessie,
You won’t be able to use the Wilcoxon Rank Sum Table with such a high value for N2. Instead you use the normal approximation, which doesn’t rely on the table, as described in Example 3 of the referenced webpage.
Also the table doesn’t give you alpha. It gives you the critical values.
Charles
Thanks !
I am actually still confused here. My n1 set of data isn’t normal. and N2 since it has such a high number, we assume it to be normal. My problem is to compare the mean of this two set of data see if they are significantly different from each other.
N2 is actually my population
Bessie,
The Wilcoxon Rank Sum Test doesn’t compare the two data sets, it compares the ranks of the values in the data set. These will be approximately normally distributed (even if the original data is not normally distributed). If one set is a sample from the second set (i.e. the population), then you are violating the independence assumption of the Wilcoxon Rank Sum Test; in fact the Wilcoxon Rank Sum Test is really testing whether the two data sets come from the same population, which in this case would clearly be true since one of the sets is the population from which the other is derived.
Charles
Thanks very much!
Hello, thank you for the website. It has helped a lot in translating a lot of the formulas for these tests to excel.
I was just wondering about the calculation of the variance in example 3. Your formula for variance reads U14*T6/6. I was just wondering where the 6 came from.
As you can see from the referenced webpage the formula for the variance is n1*n2*(n1+n2+1)/12. But the formula for the mean is n1*(n1+n2+1)/2. Using simple algebra, this means that an alternative formula for the variance is mean*n2/6.
Charles
Hello again Dr. Charles,
I am in a bit of a predicament as I have some survey data in which I have sampled the same individuals both before and after, but I don’t have anyway to link their before and after results to one another (as the survey itself was anonymous). In addition, the before and after groups have different number of responses. The data is from Likert items (not scales) so I assume non parametric tests would be the way to go. My only question is would it be appropriate to use the Wilcoxon Sum rank test even though I cannot assume independent samples?The loss in power would give more conservative results, but I was wondering if another test would be more appropriate.
I assume that you are trying to see whether there is a significant difference between Before and After. I am not sure how you would test such data since the Wilcoxon Rank Sum test requires independent samples. I can’t think of another test, but frankly I haven’t had enough time to really think too much about the situation that you have described.
Charles
Charles,
This is brilliant. Thank you for all your effort.
Unfortunately I am having problems with using your functions with array formulas. A typical sample code would look like this.
{=WTEST(IF($D$28:$D$30=F$21,$C$28:$C$30),IF($D$21:$D$27=F$22,$C$21:$C$27),2)}
Have you heard of similar problems? Do you know what could cause these problems?
Thank you very much in advance.
Regards,
Nicolas
Nicolas,
Many of the functions were intended to reference specific ranges and not formulas that output arrays that are equivalent to matrices. I have begun changing these functions so that they work in array formulas of the type that you have described.
I have already revised the WTEST function, although I believe the revised version will be in the next release of the software. It is important to recall that although the formula you have written outputs a single value, it has an embedded array formula and so you must press Ctrl-Shft-Enter for it to work.
Charles
(pr is shorthand for probability)
I should note the Chi Square was significant for this test..
It seems my message wasn’t uploaded correctly, SAS generates this for the negative W value:
pr less than Z = .00001
Hi,
Suppose I have two very large samples of several thousand observations each. One sample is a few thousand larger than the other. With uneven samples, I would use the smaller W value, and refer to the critical value of the left tail. If W-smaller sample is larger than the W-critical value, I cannot reject the null hypothesis. Is that correct?
Now let’s say I am using SAS to perform the wilcoxon test. For this wilcoxon test, SAS generates this for a NEGATIVE W value:
pr Z = .00001.
Would this mean that I cannot reject the null hypothesis?
If W (smaller) < W-crit then you would reject the null hypothesis (at least based on the table of critical values that I have provided in the website). I am not familiar with how SAS performs the test, and so I can't answer your question, although it seems very surprising that SAS would generate a negative value. Charles
Hi, I am doing a wilcoxon test with two uneven samples. I don’t understand your equation in example 2:
=IF(A6””,RANK_AVG(A6,$A$6:$B$17,1),””).
What is the “” supposed to indicate.
Please help me, thank you.
Sarah
Sarah,
Text information is surrounded by quote marks in Excel. Thus “London” means the capital of the UK. When the text is empty (i.e. blank) then there is nothing between the quote marks and you see “”
Also the formula is =IF(A6<>“”,RANK_AVG(A6,$A$6:$B$17,1),””).
Charles
suppose I have two samples with unequal sizes, how can I compare them using with Wilcoxon rank sum?
Kembo,
Examples 2 and 3 on the referenced webpage compare two samples of unequal size. I suggest that you look at these.
Charles
First of all, congratulations with your site.
I have a question related to the use of the W score in the Wilcoxon rank sum test.
If you define W as the smallest of R1 and R2, why do you use a two-tailed test and not just a one tailed?
Jean-Pierre,
If n1 = n2, you will get the same test result whether you use R1 or R2. If I remember correctly one should be compared with the left critical value and the other with the right critical value. The smaller one corresponds to the left critical value, which can be compared with the values in the critical values.
This very similar to the t test where negative t value is compared with the left critical value and the positive t value is compared with the right critical value. Given symmetry to do a two-sided test you just pick one side and compare with the t-critical value determined by halving the value of alpha. A similar thing happens in the Wilcoxon Rank Sum test.
Charles
Charles:
Indeed, well explained, but I am still not sure why we cannot reject the null hypothesis (as oppose to t-test) because W = 119.5 and 115 = W-crit. According to your eariler tutorial “Hypothesis Testing”, my understanding is to reject the null hypothesis since W-value is within the critical region.
For this and other non-parametric tests the critical region is the area less than the critical value. You can think of W-crit as the critical value on the left tail.
Charles