Trinomial Test

Basic Concepts

The trinomial test provides similar functionality to the sign test but has the advantage of better utilizing data pairs of equal value (i.e. ties), thereby achieving better statistical power than the sign test.

For the paired version of this test, with samples {x₁, …, x_n} and {y₁, …, y_n}, we define z_i = x_i – y_i. For the one sample version with median med, we define z_i = x_i – med. We now define n+ = # of z_i > 0, n– = # of z_i < 0 and n0 = # of z_i = 0, and so n = n+ + n– + n0.

We now define p₀ = n0/n and p(z) for z = 0, …, n, based on a trinomial distribution, by

Also p(-z) = p(z) for such z. For any z = d (where d = |n+ – n-|), we have a significant result when P(d) < α in a one-tailed test or P(d) < α/2 (or equivalently, 2P(d) < α) for a two-tailed test where

Example

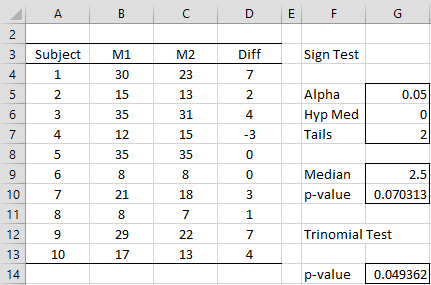
Example 1: Use the trinomial test to determine whether the population medians of the variables M1 and M2 are significantly equal based on the sample shown in columns B and C of Figure 1.

Figure 1 – Sign and trinomial tests

The null hypothesis is H₀: μ₁ = μ₂ and the alternative hypothesis is H₁: μ₁ ≠ μ₂, and so we conduct a two-tailed test. It follows that n = 10, n+ = 7, n– = 1, n0 = 2, and so d = |n+ – n-| = 6 and p0 = 2/10 = .2.

The sign test supports the null hypothesis since p-value = .070. We now show how to conduct the trinomial test to obtain a significant result where p-value = .049.

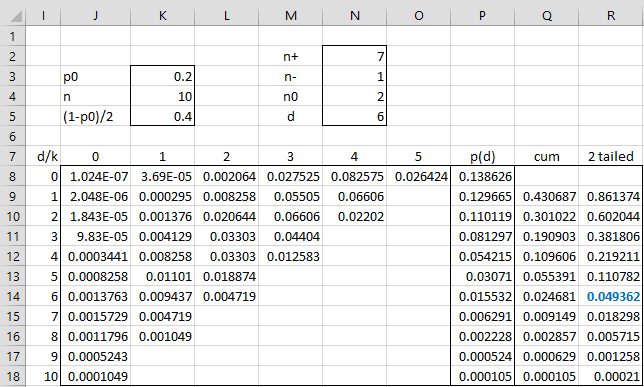
The calculations for the trinomial test are displayed in Figure 2.

Figure 2 – Trinomial Test

We calculate p(d) for d = 0, …, 10. We begin by placing the following formula in cell J8.

=IFERROR(FACT($K$4)/(FACT($I8+J$7)*FACT(J$7)*FACT($K$4-$I8-2*J$7))*$K$5^($I8+2*J$7)*$K$3^($K$4-$I8-2*J$7),””)

We then highlight the range J8:O18 and press Ctrl-R and Ctrl-D. Next, we place the formula =SUM(J8:O8) in cell P8, highlight the range P8:P18 and press Ctrl-D.

We now calculate the P(d) values by placing the formula =P18 in cell Q18 and the formula =P9+Q10 in cell Q9. Next, we highlight the range Q9:Q17 and press Ctrl-D. Since we are conducting a two-tailed test, we double the values in column Q and insert these values in column R. Since d = 6, we see that p-value = .049362, as shown in cell R14.

Worksheet Functions

Real Statistics Functions: The following functions are provided in the Real Statistics Pack:

TRINOM_TEST(d, n0, n, tails) = p-value for the trinomial test where d, n0 and n are as described above

TrinomTest(R1, R2, tails) = p-value of the trinomial test for the data in R1 and R2

TrinomTest(R1, med, tails) = p-value of the trinomial test for the data in R1 versus the median med (default = 0).

Here, tails = 1 or 2, default = 1.

For Example 1, TRINOM_TEST(6, 2, 10, 2) = .049362. Similarly, TrinomTest(B4:B13, C4:C13, 2) = .049362. In fact, it is also the case that TrinomTest(D4:D13, 0, 2) = .049362.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

Bian, G., McAleer, M., Wong, W-K (2009) A trinomial test for paired data when there are many ties
https://econpapers.repec.org/RePEc:eee:matcom:v:81:y:2011:i:6:p:1153-1160