Permutation Test for Two Independent Samples

Basic Concepts

We now present the permutation test for two independent samples. This non-parametric test does not make assumptions about normality, homogeneity of variances, or the shape of the underlying distribution. For this test, the null hypothesis is

         H0: the two samples are taken from populations with the same mean

The data in the two samples must at least have interval measurements. We demonstrate how this test is conducted via the following example.

Example

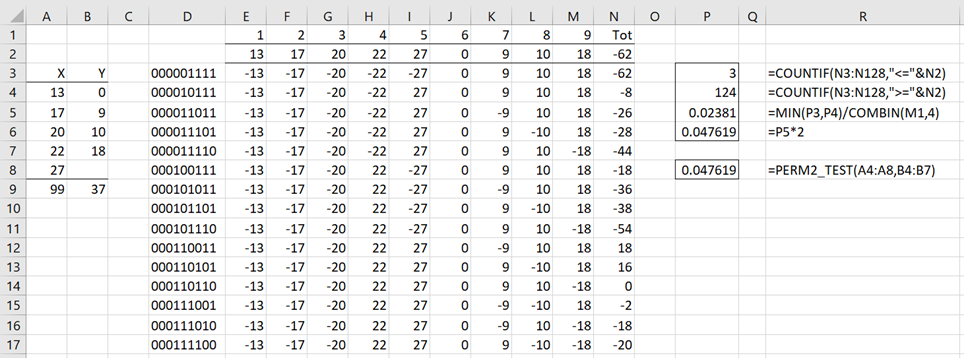
Example 1: Nine students are randomly assigned to treatment groups X and Y, 5 to X, and 4 to C, with their scores shown in columns A and B of Figure 1. Determine whether there is a significant difference in the means of the population from which the samples were drawn.

Figure 1 – Two independent sample permutation test

If the null hypothesis holds then we can view the nine sample scores as coming from the same population, and so any partition of the 9 scores between samples X and Y is equally likely. There are C(9,4) = 126 such partitions. For each partition, we will use the sum of the scores in Y minus the sum of the scores in X as the test statistic. For the observed scores, this 37 – 99 = -62.

We place the X scores in range E2:I2 and the Y scores in range J2:M2. The test statistic is then calculated by =SUM(J2:M2)-SUM(E2:I2) with the value -62 shown in cell N2. This is the same as adding all 9 scores except that the signs of the first 5 scores are flipped (as shown in range E3:N3).

Generating partitions

All the other 125 partitions are formed by changing the sign of any 5 of the scores in E2:I2 and calculating the sum. This represents partitions of the “+” and “-“ signs so that there are always 4 “+” signs and 5 “-“ signs. The first 15 such partitions are shown in Figure 1. Range D3:N130 contains the full set of data.

To perform this in Excel we insert the Real Statistics formula =INIT_SPLIT(9,5) in cell D3 and =NEXT_SPLIT(D3) in cell E3 (see Guttman Reliability), highlight range D3:D139, and press Ctrl-D. We next place the formula =E$2*(2*MID($D3,E$1,1)-1) in cell E3, highlight range E3:M3, and press Ctrl-R. To get the totals, we place the formula =SUM(E3:M3) in cell N3. Finally, we highlight range D3:N130 and press Ctrl-D.

Obtaining the p-value

This approach is similar to that employed for the paired samples permutation test. From cell P3, we see there are only 3 totals less than or equal to the observed total of -62 (cell N2). Thus, the left-tail p-value is 3/126 = .02381. The right-tail p-value is 124/126 =.984127. Generally, we are interested in the smaller of these values for the one-tailed test (as shown in cell P5). We double this number for the two-tailed test (as shown in cell P6).

Worksheet Function

Real Statistics Function: The Real Statistics Resource Pack provides the following function.

PERM2_TEST(R1, R2, tails) = the p-value of the permutation test for the data in arrays R1 and R2. If tails = 1 then the smaller one-tailed p-value is returned and if tails = 2 (default) then the two-tailed p-value is returned. If tails = -1 then the larger one-tailed p-value is returned.

R1 and R2 must be column arrays or ranges with no missing data.

We can obtain the one-tailed p-value of .02381 for Example 1 by using the formula =PERM2_TEST(A4:A8,B4:B7,1). You need to double this value to obtain the two-tailed p-value. It can also be calculated via the formula =PERM2_TEST(A4:A8,B4:B7).

One further note: This test is quite resource intensive and should only be used with relatively small samples. E.g. on my computer, the PERM2_TEST for two samples each with 13 elements takes just under the same amount of time for PERM_TEST on 25 pairs.

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

Siegel, S., Castellan, N. J. (1988) Nonparametric statistics for the behavioral sciences, 2nd ed.
https://psycnet.apa.org/record/1988-97307-000