Basic Concepts
For a sequence of numeric data, the runs test can be used to test for randomness based on the sign of the data elements. The runs up/down test, however, uses + when the sequence increases and – when the sequence decreases. In this case, for sequences that are large enough the number of runs follows a normal distribution N(μ, σ2) with
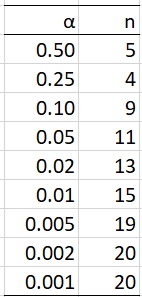
The normal approximation is valid for a two-tailed test for samples of size n at least as large as the value in the following table (divide the alpha value by 2 for a one-tailed test):
Figure 1: Normal approximation sample size requirements
Example
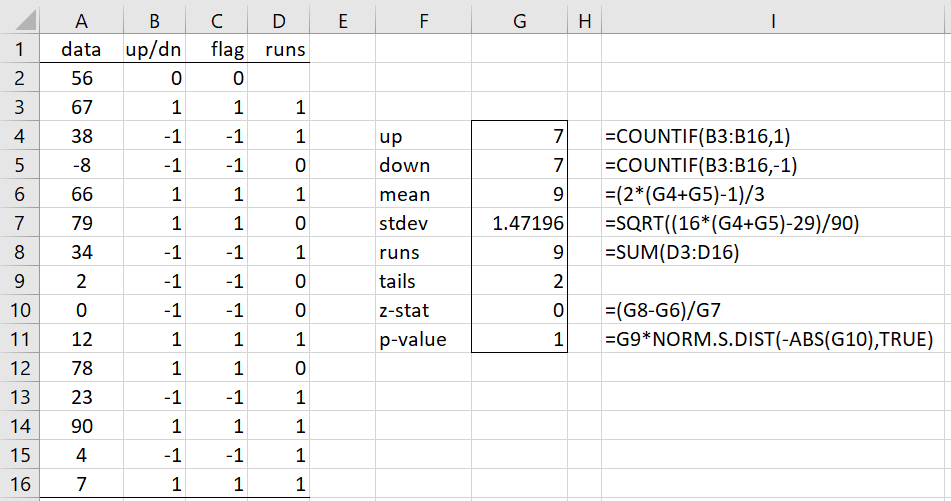
Example 1: Repeat Example 1 of One-Sample Runs Test using the runs up/down test.
The result is shown in Figure 2. We can’t reject the null hypothesis that the data sequence is random with p-value = 1 (cell G11).
Figure 2 – Runs Up/Down Test
Columns B, C, and D are used to calculate the number of runs (in cell G8). We do this by inserting 0 in cells B2 and C2, and then the formulas =IF(A3>A2,1,IF(A3=A2,0,-1)) in cell B3, =IF(B3=0,C2,B3) in cell C3, and =IF(C3<>C2,1,0) in cell D3. Finally, you highlight the range B3:D16, and press Ctrl-D.
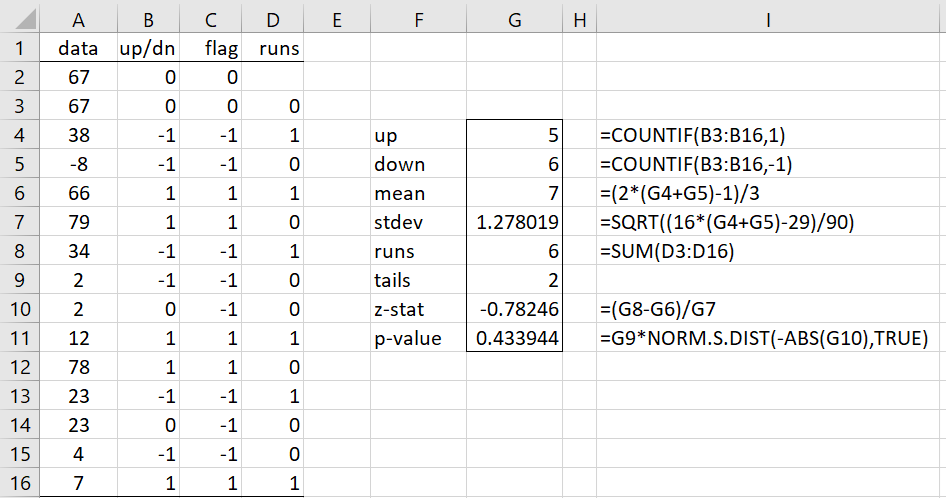
Example 2: Repeat Example 1 with the modified data in Figure 3. Note that this time there are 3 ties.
Once again, we can’t reject the null hypothesis that the data sequence is random with p-value = .433944 (cell G11).
Figure 3 – Runs Up/Down Test with ties
Worksheet Function
Real Statistics Function: The Real Statistics Resource Pack provides the following worksheet function.
RunsUpDn(R1, lab, tails): returns a column array with the results of the runs up/down test for the data in column array R1.
lab and tails are as for RUNSTEST. Also, the output has the same format as the output from RUNSTEST.
You can obtain the output shown in F4:G11 in either Figure 2 or 3 by using the array formula =RunsUpDn(A2:A16,TRUE).
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Becketti, S. (2023) Runtest. Stata
https://www.stata.com/manuals/rruntest.pdf
Zar. J. H. (2010) Biostatistical analysis 5th Ed. Pearson
https://bayesmath.com/wp-content/uploads/2021/05/Jerrold-H.-Zar-Biostatistical-Analysis-5th-Edition-Prentice-Hall-2009.pdf