Runs Distribution

Basic Concepts

Suppose there are n₁ elements of one type (say 1) and n₂ of the other type (say 2) and let x be the random variable equal to the number of runs. We now describe the (discrete) distribution function of x.

First, note that P(x = r) = the # of permutations that result in r runs divided by the # of permutations of  1’s and  2’s. The denominator is the number of ways of placing n₁ 1’s in the n₁+n₂ positions, i.e. C(n₁+n₂, n₁). The formula for the numerator is more complicated.

We ignore the case where r = 1 since this only occurs if n₁ = 0 or n₂ = 0.

Even Case

Suppose that r is even. Thus r = 2m for some positive integer m. Ignoring the repetitions of the 2’s for a moment and assuming that the first number in the sequence is a 1 we count the number of sequences with r runs. Since 1 is in the first position 2 must be in the last position (for r to be even), and so the problem is equivalent to counting the number of ways of placing exactly one 2 after m−1 of the n₁−1 1’s. This is C(n₁−1, m−1).

E.g. if n₁ = 7 and n₂ = 4 then runs of length 8 can be achieved as follows

12111211212, 11121212112, etc.

If instead, the first number in the sequence is a 2 then the last number is a 1, and so the problem is equivalent to counting the number of ways of placing exactly one 2 before m-1 of the n₁-1 1’s, which is again C(n₁−1, m−1). Thus if r is even we have 2⋅C(n₁−1, m−1) possibilities.

We next need to account for the fact that there can be multiple 2’s in sequence. The same logic shows that there are C(n₂−1, m−1) ways of distributing the 2’s (treating the sequences of 1’s as the spacers between sequences of 2’s).

Thus if r = 2m there are 2⋅C(n₁−1, m−1) ⋅C(n₂−1, m−1) ways of obtaining r runs. Thus

Odd number of runs

If r is odd then r = 2m+1 for some positive integer m. The approach is the same, except that this time sequences must begin and end with the same number. Suppose that the sequence begins (and ends) with a 1.  Since we must insert one extra 2 (compared to the case where r is even), we have C(n₁−1, m) possible sequences where a single 2 acts as a spacer between sequences of 1’s.

Once again there are C(n₂−1, m−1) ways of distributing the 2’s and so there are C(n₁−1, m) ⋅ C(n₂−1, m−1) ways of obtaining r runs if the first in the sequence is a 1. Similarly, if the first in the sequence is a 2 then there are C(n₂−1, m) ⋅ C(n₁−1, m−1) ways of obtaining r runs. Thus

Note that if n₁ ≥ n₂ then the maximum value of r is 2n₂+1. Note that the above formula works fine as long as  C(n₂−1, m) = C(m−1 m) = 0. Unfortunately, the Excel formula =COMBIN(a,b) returns an error if a < b.

Example

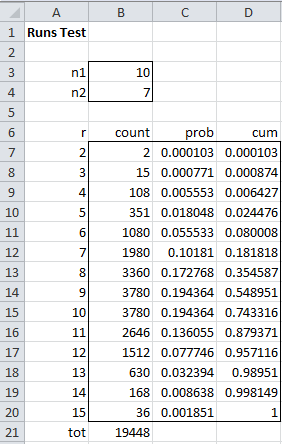
Example 1: Is 22211121121221111 a random sequence?

Here n₁ = 10, n₂ = 7 and r = 8. Using the above formulas we can create the worksheet shown in Figure 1.

Figure 1 – Runs Test

The maximum number of runs is 2n₂+1 = 2(7)+1 = 15. Some sample formulas are shown in Figure 2.

Cells	Item	Formula
B18	r = 13 (odd)	=COMBIN(B$3-1,QUOTIENT(A18,2))*COMBIN(B$4-1,QUOTIENT(A18,2)-1)+COMBIN(B$4-1,QUOTIENT(A18,2))*COMBIN(B$3-1,QUOTIENT(A18,2)-1)
B19	r = 14 (even)	=2*COMBIN(B$3-1,QUOTIENT(A19,2)-1)*COMBIN(B$4-1,QUOTIENT(A19,2)-1)
B20	r = 15 (last)	=COMBIN(B$3-1,QUOTIENT(A20,2))
B21	max	=SUM(B7:B20) or =COMBIN(B3+B4,B3)
C18	P(r = 13)	=B18/B21
D18	cdf at r = 13	=C18+D17

Figure 2 – Sample formulas from Figure 1

If we perform a two tailed test with α ≈ .05, from Figure 1 we see that P(r ≤ 5) = .0245 and P(r ≥ 13) = 1 – .990 = .010, but P(r ≤ 6) = .080 and P(r ≥ 12) = 1 – .957 = .043.  Thus, we can’t reject the null hypothesis that the sequence of values is random for any values of r in the interval [6, 12], while we reject the null hypothesis for values of r outside this interval. For Example 1, r = 8, which is inside this interval, and so we cannot reject the null hypothesis that the sequence is random.

Worksheet Functions

Real Statistics Functions: The following functions are provided in the Real Statistics Pack:

RUNSDIST(r, n1, n2, cum) = the probability density function value at r of the runs distribution (i.e. the probability that there are r runs in a sequence of n1 of one type and n2 of the other type) when cum = FALSE and the corresponding cumulative probability distribution value at r (i.e. the probability there are at most r runs) when cum = TRUE.

RUNSINV(p, n1, n2) = the critical value; i.e. the smallest value of r such that RUNSDIST(r, n1, n2, TRUE) ≥ p.

Observations

For the table lookup functions RLowerCRIT and RUpperCRIT, defined in Single Sample Runs Test, the following equalities hold.

RLowerCRIT(n1, n2, α, 1) = RUNSINV(α, n1, n2)

RUpperCRIT(n1, n2, α, 1) = RUNSINV(1−α, n1, n2)

RLowerCRIT(n1, n2, α, 2) = RUNSINV(α/2, n1, n2)

RUpperCRIT(n1, n2, α, 2) = RUNSINV(1−α/2, n1, n2)

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

Mehta, C. R. and Patel, N. R. (2013) IBM SPSS exact tests
https://www.ibm.com/docs/en/SSLVMB_27.0.0/pdf/en/IBM_SPSS_Exact_Tests.pdf