In Tolerance Interval for Normally Distributed Data we show how to calculate a tolerance interval for data that is normally distributed. We now show how to create a tolerance interval for data that is not necessarily normally distributed using a non-parametric approach.
One-sided tolerance interval
To find a lower-limit tolerance interval based on data x1, …, xn in ascending order, set
L = n – BINOM.INV(n, p, 1-α)
The 1-α tolerance interval containing p% of the population is (xL, ∞).
Similarly, an upper-limit tolerance interval is (–∞, xU) where
U = 1 + BINOM.INV(n, p, 1-α)
Either of these tolerance intervals exists only if the sample size is sufficiently large, namely
n ≥ LN(α)/LN(p)
Two-sided tolerance interval
The two-sided tolerance interval is (xL, xU) where
v = n – BINOM.INV(n, p, 1-α)
L = INT(v/2) U = INT(n + 1 – v/2)
Note that if v < 2, then the tolerance interval doesn’t exist.
Also, the tolerance interval exists only if the sample size is sufficiently large, namely, n satisfies the following inequality:
α ≥ pn-1[n – (n–1)p]
Example
Example 1: Determine the one-sided and two-sided tolerance intervals for the data in Figure 1 where p = .90 and α = .01.
Figure 1 – Data for tolerance interval
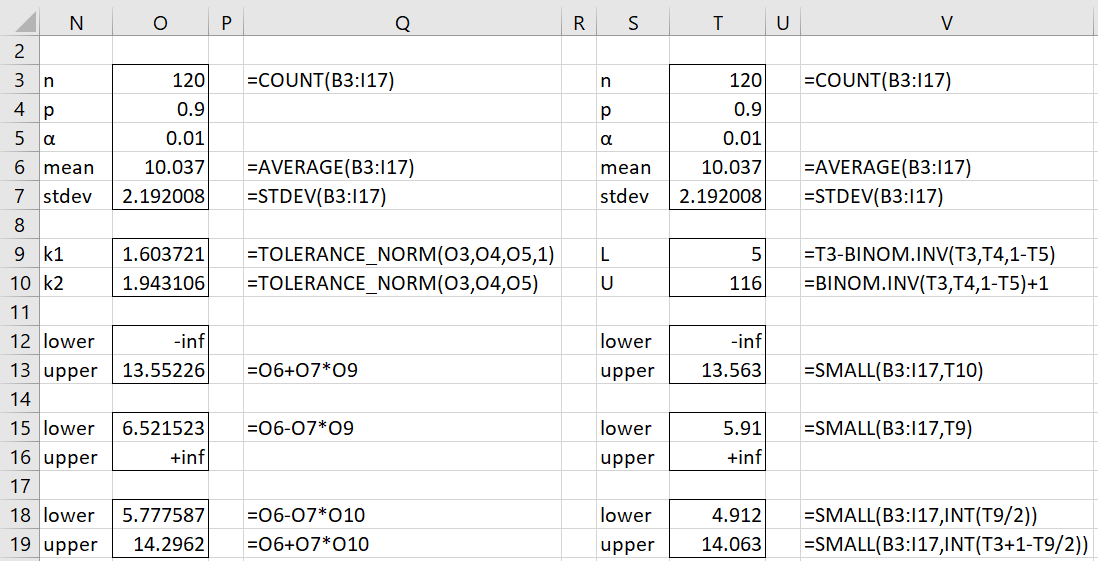
We see from the right side of Figure 1 that the data is normally distributed. We, therefore, create tolerance intervals based on the approach described in Tolerance Interval for Normally Distributed Data. This is shown on the left side of Figure 2. The two-sided tolerance interval is (5.78, 14.30), while the left-sided tolerance interval is (6.52, ∞) and the right-sided interval is (–∞, 13.55).
Figure 2 – Tolerance Interval
Even if the data were not normally distributed, we could use the non-parametric approach, as shown on the right side of Figure 2. This time, the two-sided tolerance interval is (4.91, 14.06), while the left-sided tolerance interval is (5.91, ∞) and the right-sided interval is (–∞, 13.56).
Since 120 = n ≥ LN(α)/LN(p) = LN(.01)/LN(.9) = 43.708, the one-sided non-parametric intervals are valid. Since .01 = α ≥ pn-1[n – (n–1)p] = 4.63E-05, the two-sided tolerance interval is also valid. It turns out that the minimum sample size for the two-sided tolerance interval is 64.
Real Statistics Support
Click here for information on how to construct tolerance intervals for both normally distributed data and non-normally distributed data in Excel using Real Statistics functions.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
Reference
JMP (2020) Tolerance intervals. SAS
https://www.jmp.com/support/help/en/15.1/index.shtml#page/jmp/tolerance-intervals-2.shtml#