Mann-Whitney Exact Test

Basic Concepts

Based on the relationship between the Mann-Whitney Test and the Wilcoxon Rank-Sum Test, we can modify the exact test described in Wilcoxon Rank-Sum Exact Test to provide an exact test for Mann-Whitney. In particular, we just need to subtract m(m+1)/2 where m is the size of the smallest of the two samples, from the Wilcoxon rank-sum statistic to get the Mann-Whitney test statistic.

Thus to calculate the exact p-value for given values of U, n1, and n2, we can use the formula

=PERM2DIST(U+COMBIN(MIN(n1, n2)+1, 2), cum, FALSE)

Similarly, we can calculate the (exact) critical value U_crit for given values of α, n1, and n2 via the formula

=PERM2INV(α, n1, n2, FALSE) – COMBIN(MIN(n1, n2)+1, 2)

These are the values produced by the formulas =PERM2DIST(U, n1, n2, cum) and =PERM2INV(α, n1, n2).

Worksheet Functions

Real Statistics Functions: The Real Statistics Resource Pack contains the following functions which implement the exact p-value and critical value for the Mann-Whitney test.

PERM2DIST(x, n1, n2, cum) = value of the Mann-Whitney version of the two-sample permutation distribution at x based on n1  and n2 elements; returns the pdf value if cum = FALSE and the cdf value if cum = TRUE (default).

PERM2INV(p, n1, n2) = inverse of the Mann-Whitney version of the two-sample permutation distribution at p; i.e. the least value of x such that PERM2DIST(x, n1, n2, TRUE) ≥ p.

These are the same worksheet functions described in Wilcoxon Rank-Sum Exact Test, except that in the last argument, FALSE is replaced by TRUE. If this argument is omitted, it defaults to TRUE, representing the Mann-Whitney exact test.

The Real Statistics Resource Pack also supports the following worksheet functions:

MWDIST(x, n1, n2, tails) = value of the Mann-Whitney distribution at x based on n1 and n2 elements, where tails = 1 (default) or 2. This is the p-value as defined above

MWINV(p, n1, n2, tails) = inverse of the Mann-Whitney distribution at p. This is the least value of  x such that MWDIST(x, n1, n2, tails) ≥ p, where tails = 1 (default) or 2; i.e. U-crit as defined above

MW_EXACT(R1, R2, tails) = p-value of the Mann-Whitney exact test on the data in R1 and R2, where tails = 1 or 2 (default)

Observations

Note that if x < (n1*n2)/2, then

MWDIST(x, n1, n2, 1) = PERM2DIST(x, n1, n2)

MWDIST(x, n1, n2, 2) = 2*PERM2DIST(x, n1, n2)

while if x ≥ (n1*n2)/2, then

MWDIST(x, n1, n2, 1) = 1–PERM2DIST(x, n1, n2)

MWDIST(x, n1, n2, 2) = 2*(1–PERM2DIST(x, n1, n2))

Also, if p ≤ .5, then

MWINV(p, n1, n2, 1) = PERM2INV(p, n1, n2)

MWINV(p, n1, n2, 2) = PERM2INV(p/2, n1, n2)

while if p > .5, then

MWINV(p, n1, n2, 1) = PERM2INV(1–p, n1, n2)

MWINV(p, n1, n2, 2) = PERM2INV((1–p)/2, n1, n2)

Thus for the two-tailed test for Example 1 of Mann-Whitney Test, we have

MWDIST(H11,H5,I5,2) = .1037

MWINV(.05,H5,I5,2) = 33

MW_EXACT(A6:A17,B6:B16,2) = .1037

Recursive Approach

The approach described in Wilcoxon Rank-Sum Exact Test for manually calculating the exact p-values is quite slow. Instead, we can use the following properties to recursively perform the calculations.

For samples of size m and n, the sampling frequency of the U statistic f_m,n(U) has the following property when m > 1 and m ≤ n:

where U takes values between 0 and mn. Also, define f_m,n(U) = f_n,m(U) when n < m and

Example

Example 1: Calculate the frequency function f_3,4(U) for all possible values of U.

U takes values from 0 to 3∙4 = 12. Since 4 is the larger of the two sample sizes we need to calculate the values of f_m,n(U) for all values of m = 1, 2, 3 and n = 1, 2, 3, 4 where m ≤ n and for all values of U = -4, -3, …, 11, 12. This is shown in Figure 1.

Figure 1 – Mann-Whitney Exact Test

We start by filling in the value of zero for U < 0 (columns D through G). We next fill in the values for row 4, namely 1 for U = 0, 1, 2 = n, and 0 elsewhere. The values for rows 5 and 6 are similar.

For row 7, we use the fact that f_2,2(U) = f_1,2(U-2) + f_2,1(U) = f_1,2(U-2) + f_1,2(U). This is implemented by placing the formula =F4+H4 in cell H7, highlighting the range H7:T7, and pressing Ctrl-R. For row 8, we use the fact that f_2,3(U) = f_1,3(U-3) + f_2,2(U), and place the formula =E5+H7 in cell H8, highlight H8:T8 and press Ctrl-R. Rows 9, 10, and 11 are filled in a similar manner.

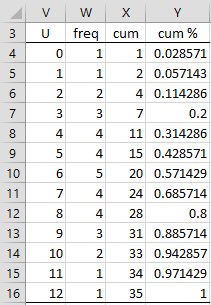
From row 11, we get the frequencies and cumulative distribution values for samples of size 3 and 4, as shown in Figure 2.

Figure 2 – Exact distribution

Column V is the transpose of H3:T3 from Figure 1 and column W is the transpose of H11:T11 from Figure 1. As usual, column X is calculated by placing the formula =X3+W4 in cell X4, highlighting the range X4:X16, and pressing Ctrl-D. Column Y is calculated by placing the formula =X4/X$16 in cell Y4, highlighting range Y4:Y16, and pressing Ctrl-D.

Note that =PERM2DIST(9,3,4) has the value .885714, as shown in cell Y13 of Figure 2. Also =MWDIST(4,3,4,2) has the value 2*.314286 = .62857.

Worksheet Array Function

Real Statistics Function: The Real Statistics Resource Pack contains the following array function that calculates the complete range of exact p-values for the specified sample sizes.

PERM2_DIST(n1, n2, cum) returns a column array with the p-values of the Mann-Whitney exact test for values of U from 0 to n1*n2  when cum = TRUE (default) and the frequency values when cum = FALSE.

The formula =PERM2_DIST(3,4) returns the array in range Y4:Y16 of Figure 2 and the formula =PERM2_DIST(3,4,FALSE) returns the array in range W4:W16.

As observed in Wilcoxon Rank-Sum Exact Test, the functions PERM2DIST, PERM2INV, MWDIST, MWINV, MW_EXACT, and PERM2_DIST work pretty well where the smaller of n1 and n2 is at most 300 while the larger is at most 1,000. You will be able to use larger sample sizes, but calculation times may become unacceptably long or overflow errors may occur.