Basic Concepts
Cliff’s Delta effect size is another measurement that can be used to estimate the effect size for an experiment comparing two samples with ordinal data.
Suppose that we have two samples X = {x1, …, xm} and Y = {y1, …, yn}. Define the delta function as follows
Cliff’s delta effect size is then defined by
Clearly, -1 ≤ δ ≤ 1. Values near ±1 indicate the absence of overlap between the two samples, while values near zero indicate a lot of overlap between the two samples.
Example
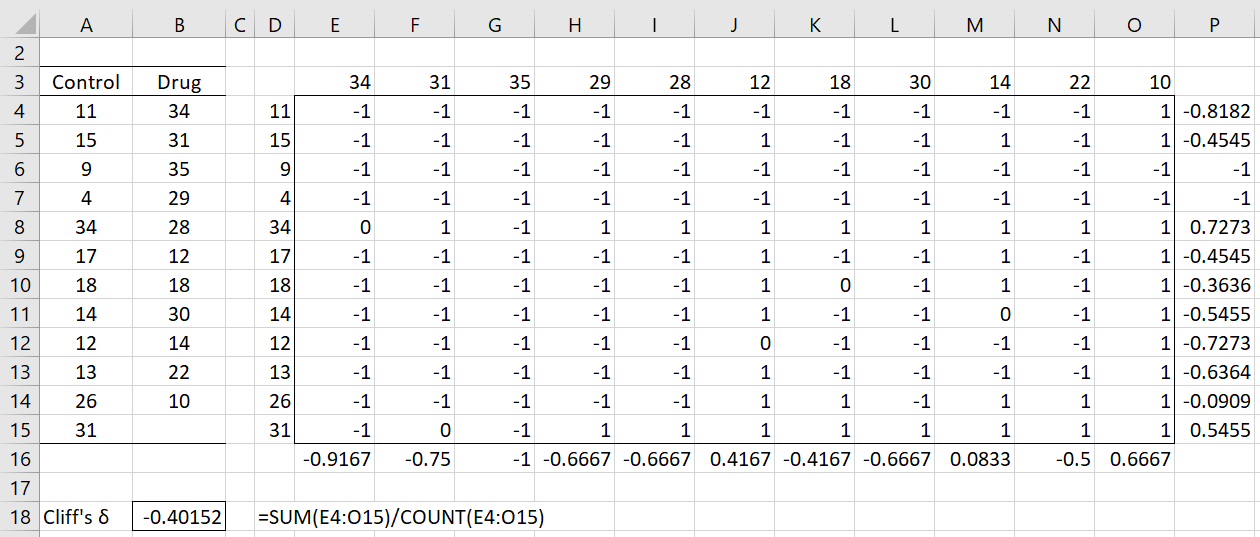
Example 1: Calculate Cliff’s Delta for the data in Example 1 of Mann-Whitney Test (repeated in range A3:D15 of Figure 1).
Construct the matrix shown on the right side of Figure 1. The delta function is implemented by placing the formula =SIGN($D4-E$3) in cell E4, highlighting the range E4:O15, and pressing Ctrl-R and Ctrl-D.
Figure 1 – Cliff’s Delta
Cliff’s Delta is now calculated using the worksheet formula =SUM(E4:O15)/COUNT(E4:O15) in cell B17, obtaining the effect size of -0.40152. This is a relatively large effect with larger values tending to be in the Drug sample (since the sign is negative).
Standard Error
The standard error for Cliff’s Delta is given by the formula
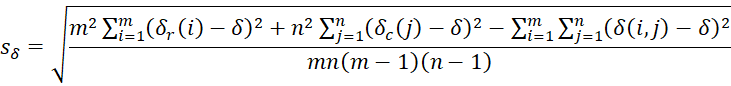 where
where![]()
Actually, the minimum value of the variance of δ is set to (1-δ2)/(mn-1).
Confidence Interval
The symmetric confidence interval is
![]()
where zcrit = NORM.S.INV(1-α/2). A more accurate estimate of the confidence interval is
Another Example
Example 2: Calculate the standard error of Cliff’s Delta for the data in Example 1 as well as a 95% confidence interval.
The standard error is .225 as shown in Figure 2. The symmetric confidence interval is (-842, .0388) and the improved confidence interval is (-.730, .0778).
Figure 2 – 95% confidence interval for Cliff’s Delta
Note that column W displays the formulas in column S.
Worksheet Function
Real Statistics Function: The Real Statistics Resource Pack provides the following function:
CLIFF_DELTA(R1, R2, lab, alpha, sym): returns a column array containing Cliff’s delta for the samples in R1 and R2, the standard error and lower and upper limits of the 1-alpha confidence interval; if lab = TRUE (default FALSE) then a column of labels is appended to the output; alpha defaults to .05; if sym = TRUE (default FALSE) then a symmetric confidence interval is returned
For Example 1, =CLIFF_DELTA(A4:A15,B4:B14) generates the value shown in cell B18. The array function CLIFF_DELTA can also be used to calculate the standard error and confidence interval, as shown in Figure 3.
Figure 3 – CLIFF_DELTA array function
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Cliff, Norman (1993). Dominance statistics: Ordinal analyses to answer ordinal questions. Psychological Bulletin. 114 (3): 494–509
Feng, D. and Cliff, N. (2009) JMASM29: Dominance analysis of independent data (Fortran)
https://core.ac.uk/download/56683109.pdf
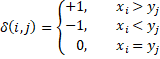
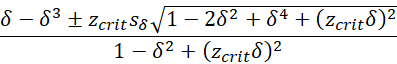


dear mr. Zaiontz,
In the example in cell T7 the squared deviations from E16 till O16 is calculated, however this will then use the average from E16 till O16, which is the negative version of cliff delta, not the regular one.
According to the formula it should be the overall delta.
Is the formula incorrect, or the calculation? Or am I missing something else?
Kind regards,
Peter
nevermind 🙂 figured it out
Good to hear