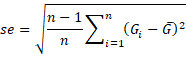Standard Error of Gini Index

Jackknifing

We can use a procedure called jackknifing to create a 1–α confidence interval for the population Gini coefficient. In this procedure, G = the Gini coefficient for the sample and we define the Gini coefficient G_i which results from the sample where i^th sample element is deleted. The jackknifed estimate of the population Gini coefficient is defined by

The standard error for G* can be estimated as

where G-bar is the average of the G_i values; i.e.

Bootstrapping

Alternatively, we can use the bootstrap method described in Resampling. This is accomplished by drawing k subsamples of size n with replacement from the original sample. For each subsample, we calculate the Gini coefficient G_j. We can use the following estimator of the standard error for G.

where G-bar is the average of the k G_j values; i.e.

A 1–α confidence interval is given by (G’_α/2, G‘_1-α/2) where G‘_m is the m^th smallest element among the k bootstrap elements.

Bias-corrected Confidence Interval

There is also a bias-corrected confidence interval defined as (G’_p, G’_q) where

p = NORM.S.DIST(2z₀–z₁, TRUE)

q = NORM.S.DIST(2z₀+z₁, TRUE)

and

z₀ = NORM.S.INV(r)

z₁ = NORM.S.INV(1–α/2)

r = the fraction of G_j bootstrap values that are less than or equal to G

Worksheet Functions

Real Statistics Functions: The following array functions are provided in the Real Statistics Pack:

GiniTest(R1, lab, iter, alpha): outputs a 5 × 1 column range containing the Gini coefficient for the data in R1, the mean Gini coefficient from the bootstrapping with iter bootstraps, the standard error and the lower and upper ends of the 1–alpha confidence interval.

GiniUnbiased(R1, lab, iter, alpha): outputs a 7 × 1 column range containing the Gini coefficient for the data in R1, the mean Gini coefficient from the bootstrapping with iter bootstraps, the standard error, the lower and upper p-values (i.e. p and q as defined above) and the lower and upper the ends of the confidence interval described by p and q.

if lab = TRUE (default is FALSE) then an extra column of labels is added to the output. alpha defaults to .05 and iter defaults to 2000.

For Example 1 of Lorenz Curve, GiniTest(A4:A23,TRUE) yields the results shown on the left side of Figure 1 and GiniUnbiased(A4:A23,TRUE) produces the results shown on the right side of the figure.

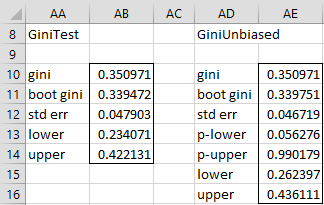
Figure 1 – Gini confidence intervals

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Mirzaei, S., Borzadaran G. R. M., Aminib, M., Jabbarib, H. (2017) A comparative study of the Gini coefficient estimators based on the regression approach. Communications for Statistical Applications and Methods. Vol. 24, No. 4, 339–351.
http://www.csam.or.kr/journal/download_pdf.php?doi=10.5351/CSAM.2017.24.4.339

Buchan, I. E. (2016) Gini coefficient of inequality. Stats Direct Limited
https://www.statsdirect.com/help/nonparametric_methods/gini_coefficient.htm