Data Analysis Tool
You can also obtain the results for both the Brunner-Munzel test and Permutation Brunner-Munzel test in Excel by using the Real Statistic Brunner-Munzel data analysis tool.
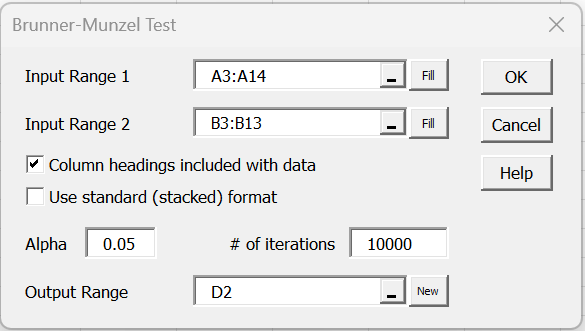
To obtain the results for Example 1 of Brunner-Munzel Test Example and Example 1 of Permutation Brunner-Munzel Test press Ctrl-m and choose the Brunner-Munzel data analysis tool from the Misc tab (or from the menu that appears if using the original user interface). Fill in the dialog box that appears as shown in Figure 1.
Figure 1 – Brunner-Munzel Test dialog box
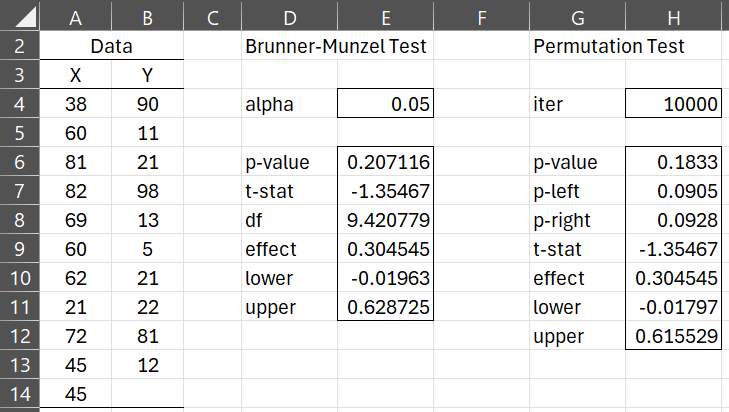
After clicking on the OK button, the output shown in Figure 2 appears.
Figure 2 – Brunner-Munzel Test data analysis
Data in stacked format
We can also use the Brunner-Munzel test for data in stacked format. For example, if data is in the format shown in D2:E22 of Figure 1 of Permutation BM Test, we could enter the range D2:E22 in Input Range 1 of the dialog box displayed in Figure 1 and check the Use standard (stacked) format option. The output will be as shown in Figure 2.
Alternatively, you can use the array formula =StdAnova1(D2:E22) to first reformat the data in stacked format to the format shown in A3:B14, and then use the Real Statistics BM_TEST and/or BM_PTEST worksheet function on the data in A3:A14 and B3:B14.
Data in frequency table format
We can also use the Brunner-Munzel test for data in frequency table format.
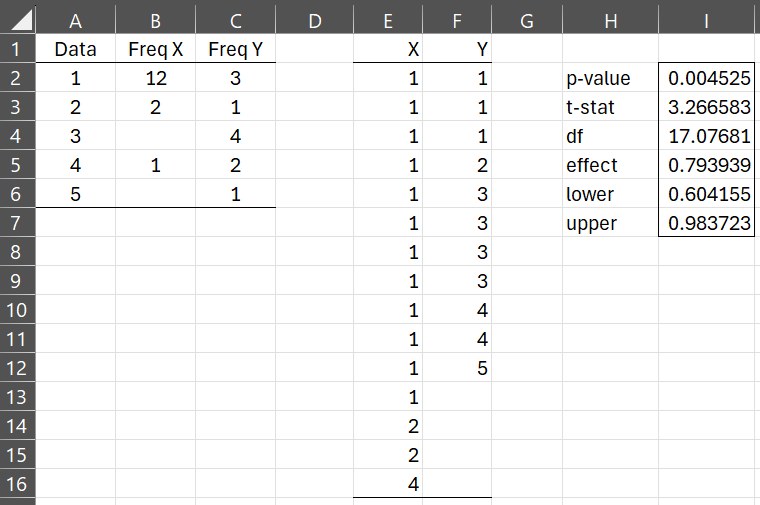
Example 1: Perform the Brunner-Munzel test on the data in range A1:C6 of Figure 3.
Figure 3 – BM Test on data in frequency format
First transform the frequency data into raw format by using the array formula =Freq2RAW(A2:B6) in range E2:E16 and =Freq2RAW(A2:A6,C2:C6) in range F2:E12. You can use the formula =BM_TEST(E2:E16,F2:F12,TRUE) to obtain the results shown in range H2:I7.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Brunner, E., Munzel, U. (2000) The Nonparametric Behrens-Fisher problem: Asymptotic theory and a small-sample approximation
https://community.jmp.com/t5/JMP-Wish-List/Brunner-Munzel-test/idi-p/631723?attachment-id=17778
Nowak, C. P., Pauly, M., Brunner, E. (2022) The nonparametric Behrens-Fisher problem in small samples
https://arxiv.org/pdf/2208.01231
Karch, J. D. (2021) Psychologists should use Brunner-Munzel’s instead of Mann-Whitney’s U test as the default nonparametric procedure.
https://osf.io/preprints/psyarxiv/kgdwn
Noguchi, K., Konietschke, F., Marmolejo-Ramos, F., Pauly, M. (2021) Permutation tests are robust and powerful at 0.5% and 5% significance levels
https://link.springer.com/article/10.3758/s13428-021-01595-5
Toshiaki A. (2022) Usage of brunnermunzel package
https://cran.r-project.org/web/packages/brunnermunzel/vignettes/usage.html
Pauly, M., Asendorf, T., Konietschke, F. (2014) Permutation tests and confidence intervals for the area under the ROC-curve
https://www.uni-ulm.de/fileadmin/website_uni_ulm/mawi.inst.105/Publikationen/FrankThomas_8.pdf
Dear Charles,
I am grateful for your thoughtful remarks.
Eiji
Dear Charles,
Thank you for implementing the Brunner-Munzel test.
Can this BM test analyze paired data?
Also, do you have any plans to implement ANOVA or multiple comparisons based on the BM test approach?
I will be waiting for your comments.
Thanks you.
Eiji
Eiji,
1. I don’t know of a version of the Brunner-Munzel test for paired data. Since there is really only one sample (i.e. the differences between the pairs), there is no need to check homogeneity of variances and so the BM test wouldn’t add anything over the usual Paired Signed Ranks test.
2. Since ANOVA assumes homogeneity of variances, its seems that the Brunner-Munzel test would not be needed as for multiple comparison testing. When there is doubt about the variances, Games-Howell is used. Perhaps there is an advantage of Brunner-Munzel over Games-Howell but I have not seen any reference to this in the literature. Whereas Games-Howell addresses experiment-wise error, it seems that something better than a Bonferroni correction would be needed with Brunner-Munzel. In any case, I like your idea, but it seems like additional work would be needed to create a multiple comparison version of Brunner-Munzel.
Charles
Dear Charles,
I am grateful for your thoughtful response.
1. The Wilcoxon signed-rank test is contingent upon the symmetry of the distribution of the difference data between pairs of data. In my experience, there is often a lack of symmetry in the difference data. The sign test does not have this restriction, but has the disadvantage of low power. Therefore, I was curious as to whether the BM test could be used for paired data. The following URL describes the BM test for paired data, and I would have liked to know if this is possible with your software.
https://search.r-project.org/CRAN/refmans/TOSTER/html/brunner_munzel.html
Does your software include a test for difference data in the absence of symmetry?
2. I am grateful for your insights on the subject of ANOVA and multiple comparisons.
I look forward to receiving your feedback.
Thank you in advance.
Eiji
Dear Eiji,
1. The only approach I can think of is to use a one-sample permutation test, although this may also require symmetry. See
https://real-statistics.com/non-parametric-tests/resampling-procedures/
https://real-statistics.com/non-parametric-tests/permutation-test-for-paired-samples/
2. One other thing: I believe symmetry is a requirement for the signed rank test only if you are testing a hypothesis about the median (or mean). I don’t think this is a requirement if your null hypothesis is that if an element x from the population is drawn at random then the probability that x > m is the same as the probability that x < m (where m is a specific value). It is worth investigating whether this is so. Charles