Basic Concepts
The Mann-Whitney test is the commonly used non-parametric substitute for the two independent t-test when the normality assumption is not met. It turns out, however, that it generally requires that the two samples come from populations with the same shape (with possible differences in location), an assumption which is rarely met. In particular, the Mann-Whitney test requires that the two populations have the same variance (or at least similar variances).
We can consider the Mann-Whitney test to be the non-parametric version of the t-test with equal variances. We now describe the Brunner-Munzel test as the non-parametric version of the t-test even with unequal variances (i.e. the nonparametric version of Welch’s t-test). Just as Welch’s t-test can be used even when the variances are equal, the same is true for the Brunner-Munzel test.
Test Overview
Suppose that you have a sample X of size m for the random variable x (group 1) and a sample Y of size n for y (group 2). The BM test is designed to test the (two-sided) null hypothesis:
H0: P(x < y) = P(y < x)
This hypothesis is called stochastic equality.
We can also test the one-sided null hypothesis
H0: P(x < y) > P(y < x)
or
H0: P(x < y) < P(y < x)
Suppose sample X = {x11, …, x1m} and sample Y = {x21, …, x2n} and let N = m+n. We also find it convenient to denote m by n1, n by n2, X by X1 and Y by X2.
Define Rij to be the rank of xij in X1 ∪ X2, Rij* to be the rank of xij in Xi, and Ri to be the average of the pooled rankings Rij.
Effect Size and Null Hypothesis
We also define the relative treatment effect size as
p = P(x < y) + .5P(x = y)
The two-sided null hypothesis is therefore equivalent to
p = .5
The one-sided null hypotheses are equivalent to p < .5 or p > .5.
The effect size p can be approximated by
We define the studentized version of p as
where
which is estimated from the samples by
where si2 is the sample variance of the Pij with
The test statistic for the BM test is
For m and n sufficiently large (each at least 10), t has a standard normal distribution. Thus, we reject the null hypothesis if |t| > tcrit = T.INV.2T(α/2, df) where
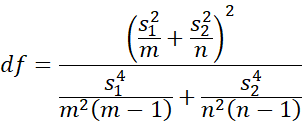
as for Welch’s t-test.
As noted previously, the MW test is the nonparametric version of the t-test with equal variances and the BM test is the nonparametric version of the t-test with unequal variances (i.e. Welch’s t-test).
Continuation
We continue the description of the Brunner-Munzel Test with the following topics:
References
Brunner, E., Munzel, U. (2000) The Nonparametric Behrens-Fisher problem: Asymptotic theory and a small-sample approximation
https://community.jmp.com/t5/JMP-Wish-List/Brunner-Munzel-test/idi-p/631723?attachment-id=17778
Nowak, C. P., Pauly, M., Brunner, E. (2022) The nonparametric Behrens-Fisher problem in small samples
https://arxiv.org/pdf/2208.01231
Karch, J. D. (2021) Psychologists should use Brunner-Munzel’s instead of Mann-Whitney’s U test as the default nonparametric procedure.
https://osf.io/preprints/psyarxiv/kgdwn
Noguchi, K., Konietschke, F., Marmolejo-Ramos, F., Pauly, M. (2021) Permutation tests are robust and powerful at 0.5% and 5% significance levels
https://link.springer.com/article/10.3758/s13428-021-01595-5
Karch, J. D. (2022) Choosing between the two-sample t test and its alternatives: a practical guide
https://osf.io/preprints/psyarxiv/ye2d4
Akinshin, A. (2023) Corner case of the Brunner-Munzel test
https://aakinshin.net/posts/brunner-munzel-corner-case/
Toshiaki A. (2022) Usage of brunnermunzel package
https://cran.r-project.org/web/packages/brunnermunzel/vignettes/usage.html
Pauly, M., Asendorf, T., Konietschke, F. (2014) Permutation tests and confidence intervals for the area under the ROC-curve
https://www.uni-ulm.de/fileadmin/website_uni_ulm/mawi.inst.105/Publikationen/FrankThomas_8.pdf
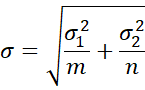
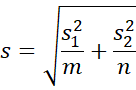
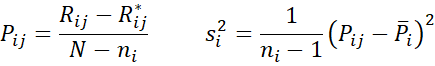
Thanks for this. Very clear. Small issue though. You write:
“For m and n sufficiently large (each at least 10), t has a standard normal distribution. Thus, we reject the null hypothesis if”
but then proceed using the t-distribution. I assume it should be that if m an n are sufficiently large we can simply use the standard normal distribution, otherwise use the t-distribution with the specified degrees of freedom?
Peter,
I am saying that if m and n are sufficiently large you use the test described based on the t distribution.
I am not stating anything if the m and n are not sufficiently large. I believe that in this case, you can use the permutation version of the test, but I need to check on this,
Charles
Dear Charles,
The quote “For m and n sufficiently large (each at least 10), t has a standard normal distribution. Thus, we reject the null hypothesis if” is from your page. So it clearly states ‘standard normal distribution’, but then you use the t-distribution. I think it should probably be:
For m and n sufficiently large (lets say 50) t has a standard normal distribution.
For m and n small (lets say at least 10) t has a t-distribution
For m and n very small a permutation version of the test could be used, or the C^2 test.
Oh, on a side note, the formula for s_i^2 seems to be missing a summation sign.