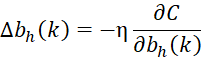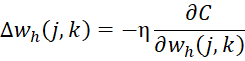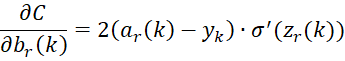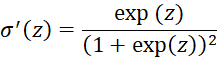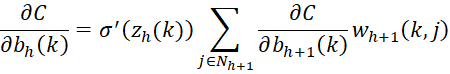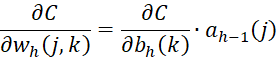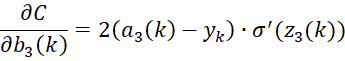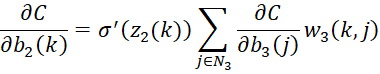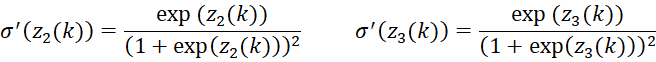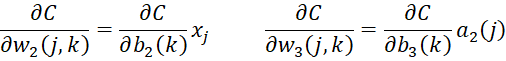Training a Neural Network

We now describe how a neural network uses backward propagation to train the network. We will use the notation and formulas from Neural Network Basic Concepts.

Initialization

Initially, all biases bh(k) and weights wh(j, k) are assigned random values (for h > 1). There are several approaches for doing this.

  • Randomly assign values from a standard normal distribution.
  • Randomly assign values from the normal distribution N(0, 1/n1) where 1/n1 is the variance and n1 is the number of input nodes.
  • Use the values from a previous run of the neural network

Iterations

In each iteration, these values are updated to be

Update bias

Update weights

where

Delta bias

Delta weight

and η > 0 is a preassigned learning rate and

output node bias change

where r = the Output Layer and

Derivative of link function

For 1 < h < r

Hidden layer bias change

For any h > 1

Weight change

Details

Those of you who are familiar with calculus recognize that the above backward propagation equalities involve partial derivatives; in fact, we can actually prove these equalities. For those of you who are not familiar with calculus or don’t care to see the proof, you can skip the following since it is not essential to understanding the functioning of the neural network; otherwise, click here.

Backpropagation for a network with one hidden layer

Output layer bias change

Hidden layer bias change

Derivative of link function

Weight change

References

Lubick, K. (2022) Training a neural network in a spreadsheet
https://www.youtube.com/watch?v=fjfZZ6S1ad4
https://www.youtube.com/watch?v=1zwnPt73pow

Nielson, M. (2019) Neural networks and deep learning
http://neuralnetworksanddeeplearning.com/

Leave a Comment