More about One Factor Multivariate Repeated Measures

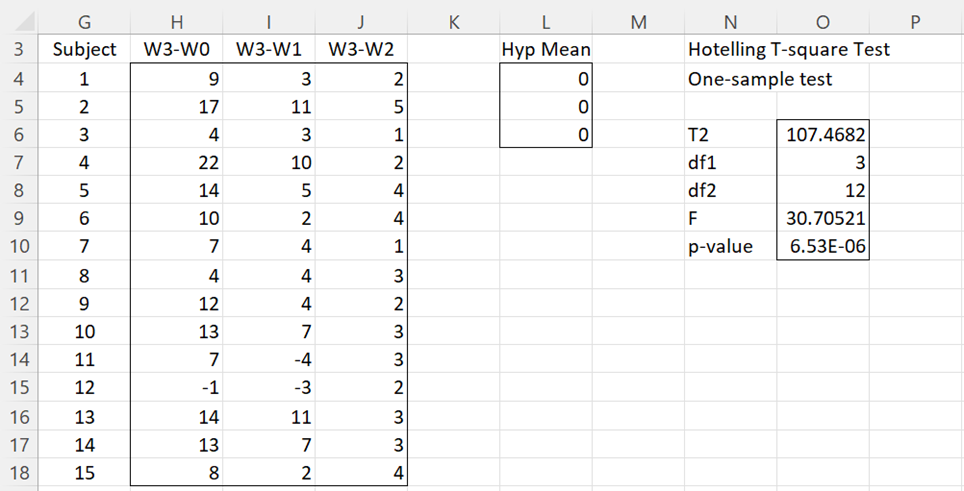
Equivalent Test Procedure

In Example 1 of One Factor Multivariate Repeated Measures, we chose to test the null hypothesis H0: μ₀ = μ₁ = μ₂ = μ₃ by testing an equivalent version of the hypothesis, namely H0: μ₁ – μ₀ = 0, μ₂ – μ₁ = 0, μ₃ – μ₂ = 0. We could instead test the equivalent null hypothesis H0: μ₃ – μ₀ = 0, μ₃ – μ₁ = 0, μ₃ – μ₂ = 0.

The data for this example is repeated in Figure 1.

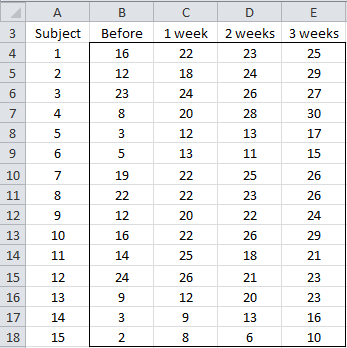
Figure 1 – Example 1 Data

The results of this test using the revised null hypothesis are shown in Figure 2.

Figure 2 – Equivalent repeated measures test

Note that the results are the same as those shown in Figure 2 of One Factor Multivariate Repeated Measures.

Test with only Two Dependent Variables

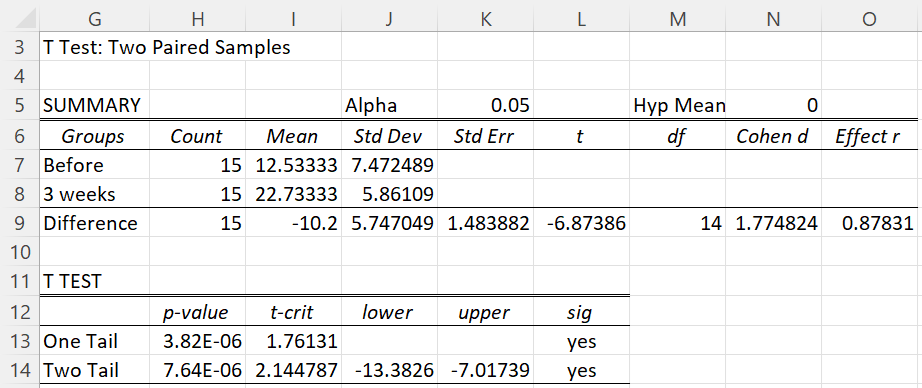
This approach works when there are 3 or more dependent variables. When there are only two dependent variables, we can use the paired t-test. E.g. if for Example 1 we only had the data before the program and 3 weeks after the start of the program (columns B and E of Figure 1), we would conduct a paired t-test (or signed-rank test if the assumptions were not met) to obtain the results shown in Figure 3.

Figure 3 – Paired t-test

This is equivalent to the test t = D/(s_D/√n) ∼ T(n–1), or even F = nD²/s_D ∼ F(1, n–1), where D = the data consisting of the differences of the values in columns B and E (i.e. the data in column H of Figure 2). Thus, the results in Figure 3 are equivalent to a one-sample t-test on the data in D.

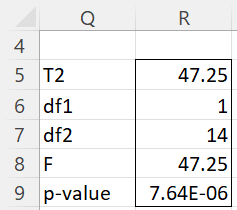
Actually, we can obtain similar results using the array formula =Hotelling(B4:B18,E4:E18,1,TRUE) or =Hotelling(H4:H13,,0,TRUE) to obtain similar results as shown in Figure 4.

Figure 4 – Hotelling’s version of the paired t-test

Links

↑ Multivariate repeated measures tests

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

References

Rencher, A.C. (2002) Methods of multivariate analysis (2nd Ed). Wiley-Interscience, New York.
http://math.bme.hu/~csicsman/oktatas/statprog/gyak/SAS/eng/Statistics%20eBook%20-%20Methods%20of%20Multivariate%20Analysis%20-%202nd%20Ed%20Wiley%202002%20-%20(By%20Laxxuss).pdf