On this webpage we describe the GHK (Geweke, Hajivassiliou and Keane) sampling algorithm and how to use it to estimate the cdf of the multivariate normal distribution (see Multivariate Normal Functions).
GHK Algorithm
Let N(μ, Σ) be a multivariate normal distribution where μ is the k × 1 mean-vector and Σ is the k × k covariance matrix. Also, let A and B be k × 1 vectors where A < B (i.e. ai < bi for all i). We can assume that μ is the zero vector.
Our goal is to create a sequence of k × 1 vectors X1, …, Xr, such that A < Xj < B for all j. We can then use this sequence to estimate P(A < X < B) via the formula
where
and the qim are defined recursively using the Cholesky decomposition of Σ = CCT. Note that cij = 0 if j > i. For i = 1, we define
and for i = 2, 3, …, k (and m = 1, …, r), define qim recursively as follows:
where Φ(x) = the standard normal distribution function at x, which can be calculated in Excel by =NORM.S.DIST(x,TRUE), and
with εhm drawn randomly from a truncated normal distribution with bounds
Example
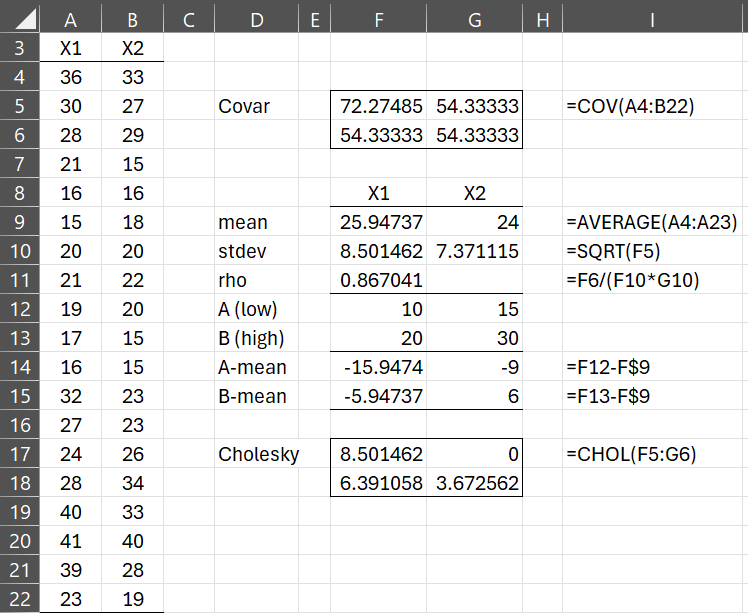
Example 1: Approximate P(A < X < B) for the bivariate normal distribution defined in Example 1 of Multivariate Normality Functions on the bounds A = (10, 15) and B = (20, 30) using the GHK algorithm with 10 samples.
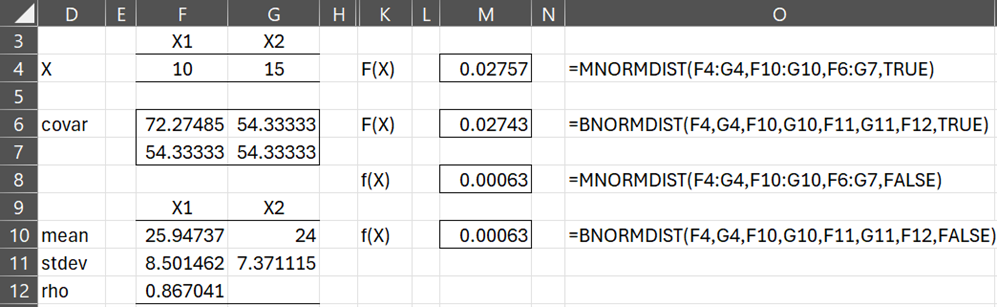
Figure 1 shows the data and associated parameters for this bivariate normal distribution.
Figure 1 – Example bivariate normal distribution
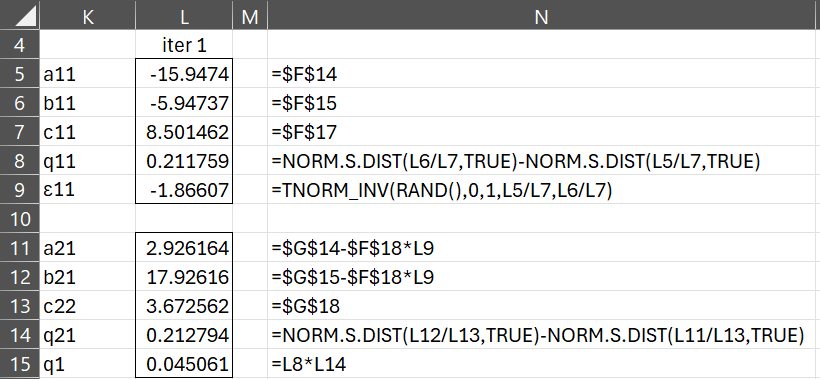
Figure 2 describes how to obtain the first sample used in the GHK algorithm.
Figure 2 – Sample 1 of GHK algorithm
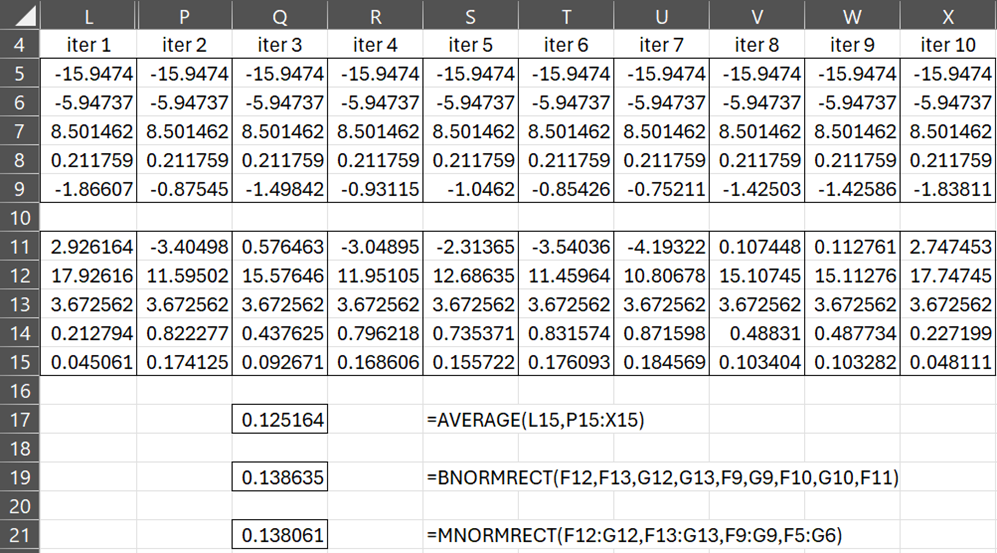
We obtain the other nine samples in exactly the same way, with the results shown in Figure 3.
Figure 3 – 10 Samples using the GHK algorithm
The estimated probability is the average of the 10 qj values in row 15, namely .125164 (cell S17). Note that if we use the Real Statistics MNORMRECT worksheet function with 200 samples (instead of 10), we obtain a better estimate of .138635 (cell S21). We can get a fairly good estimate with a relatively small sample.
We define this function momentarily. We can also use the BNORMRECT, defined in Multivariate Normal Functions, to obtain the result shown in cell S19. Of course, the advantage of the MNORMRECT function is that it applies to any multivariate normal distribution, not just bivariate normal distributions.
Multivariate Normal CDF
We can use the GHK algorithm to calculate the cumulative distribution function (cdf) of a multivariate normal distribution. To calculate the cdf F(X) for random vector X, we set the upper bound B in the GHK algorithm to X and the lower bound to A = a vector all of whose values are -∞. We can accomplish this by using a sufficiently large negative value such as -100 (or even -10) instead of -∞. Alternatively, we can replace Φ(aim/cii) by zero in the GHK algorithm.
Using the GHK algorithm in this way with 200 samples, we estimate the cdf of the multivariate normal distribution in Example 1 at X = (10, 15) to be F(X) = .02757, as shown in Figure 4.
Figure 4 – CDF using the GHK algorithm
Actually, we use the MNORMDIST worksheet function, as described below, to obtain these results. We obtain similar results using the BNORMDIST worksheet function.
Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack provides the following functions in support of multivariate normal distributions.
MNORMDIST(R0, Rm, Rc, cum, iter) = the cdf of the multivariate normal distribution at R0 if cum = TRUE and the pdf if cum = FALSE.
MNORMRECT(Rlo, Rhi, Rm, Rc, iter) = P(A < X < B) for the multivariate normal distribution where A and B are the column vectors corresponding to Rlo and Rhi.
Here, R0, Rm, Rlo, and Rhi are k × 1 arrays or cell ranges with all the elements in Rlo less than or equal to the corresponding element in Rhi. Rm represents the mean vector and Rc is the k × k covariance matrix. iter = the number of samples used in the GHK algorithm (default 200).
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Greene, W. (2012) Econometric analysis, 7th ed. Prentice Hall
Wikipedia (2024) GHK algorithm
https://en.wikipedia.org/wiki/GHK_algorithm
Shum, M. (2008) GHK description
https://www.its.caltech.edu/~mshum/gradio/ghk_desc.pdf
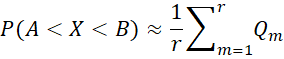
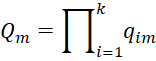
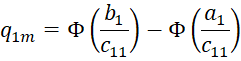
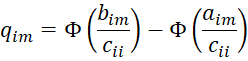
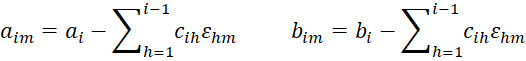
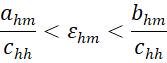
I have read that using Hammersley sequence or Halton sequence you can improve the precision of the ghk algorithm.
instead of using random numbers with uniform distribution (0,1)
Antony,
The algorithm uses TNORM_INV(RAND(),…), i.e. a random value from a truncated normal distribution. Are you saying that instead of using RAND(), which is a random value from a uniform distribution (0,1) it is better to use a random value from a Hammersley sequence or Halton sequence?
Charles
THAT’S RIGHT, USING Hammersley or Halton SEQUENCES THE ALGORITHM CAN BE IMPROVED