We can calculate power and minimum sample size for two-way MANOVA in the same manner as for one-way MANOVA (see MANOVA Power and Sample Size).
Statistical Power
Example 1: What is the power for the interaction of the two factors for the two-way MANOVA in Example 1 of Two-way MANOVA Example.
The power is 89% as calculated in cell B18 of Figure 1.
Figure 1 – Power calculation
Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack provides the following functions.
MANOVA2Row_POWER(f, n, k, g1, g2, ttype, alpha, iter, prec) = the statistical power of the first factor (aka the row factor) for two-way MANOVA where the sample size is n, the number of dependent variables is k , the number of groups in the first factor is g1, the number of groups in the second factor is g2 and the effect size is f, where f = the partial eta-square effect size if ttype = 1, f = eta-square if ttype = 2 and f = Pillai’s V if ttype = 3.
MANOVA2Row_SIZE(f, k, g1, g2, pow, ttype, alpha, iter, prec) = the minimum sample size to obtain statistical power of pow of the first factor for two-way MANOVA where f, k, g1, g2 and ttype are as for MANOVA2Row_POWER.
The Real Statistics worksheet functions MANOVA2Col_POWER, MANOVA2Int_POWER, MANOVA2Col_SIZE, MANOVAInt_SIZE for the second factor (aka the column factor) and interaction between the factors are defined similarly.
alpha is the significance level (default .05), iter = the maximum number of iterations used in calculating the answer (default 1000) up to a precision of prec (default 0.000000001), the default for pow is .80.
We can calculate the power for Example 1 by any of the following formulas (with reference to Figure 3).
=MANOVA_POWER(B5,B9,B7,B6)
=MANOVA_POWER(B4,B9,B7,B6,2,B13)
=MANOVA_POWER(B3,B9,B7,B6,3,B13)
Sample Size
Example 2: What sample size would be required to detect a partial eta-square effect size of .2 for the interaction between the two factors with power 95% if the experiment in Example 1 of Two-way MANOVA Example is to be repeated?
The required sample size is calculated as shown in cell G8 of Figure 2.
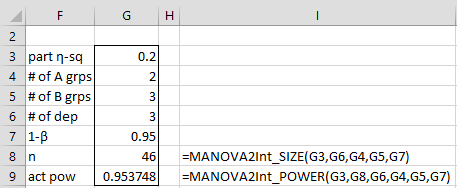
Figure 2 – Sample size calculation
As we can see, the minimum sample size is 46. Since 46 is not divisible by 2 ⨯ 3 = 6, the number of interaction groups, if we require a balanced model, then the minimum sample is 48, the next highest number larger than 46 that is divisible by 6.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Faul, F., Erdfelder, E., Buchner, A., & Lang, A. G. (2009) Statistical power analyses using G*Power 3.1: Tests for correlation and regression analyses. Behavior Research Methods, 41, 1149-1160.
http://link.springer.com/article/10.3758/BRM.41.4.1149
Hintze, J. L. (2011) Multivariate analysis of variance (MANOVA). NCSS PASS
https://www.ncss.com/wp-content/themes/ncss/pdf/Procedures/PASS/Multivariate_Analysis_of_Variance-MANOVA.pdf
