We now describe a non-parametric version of one-way MANOVA, called Permutational MANOVA, which has fewer assumptions than ordinary MANOVA.
Topics
- Basic Concepts – this webpage
- Excel Example
- Real Statistics Support
Basic Concepts
As for MANOVA, we have m random vectors X1, …, Xm (representing groups or treatments) where each Xj contains n sample elements, each consisting of a vector with k elements. We restrict the analysis to balanced models where each group contains the same number of elements. The total number of elements (i.e. k-vectors) is therefore N = mn. We next use a distance measurement dij between two k-vectors to define the total, within-group, and between-groups sum of squares as follows:
As usual, we define degrees of freedom dfT = N – 1, dfW = N – m, and dfB = m – 1. Finally, we define the corresponding MS = SS/df and a pseudo-F statistic by
Basic Approach
If the MANOVA null hypothesis is true, then we can shuffle the group labels without having a large impact on the analysis, and in particular without having a big impact on the value of the F statistic. If instead there is a significant treatment effect then the value of F based on the original groups will tend to be larger than those calculated from the permutations.
The test approach is to repeatedly and randomly permute the data rows to obtain a large number of F values, say F1, …, Fh. We also include F0 which is the F statistic for the original data without permutations. In this way, we obtain the following p-value
The null hypothesis is supported if p ≥ α while there is a significant result (indicating that there is a significant difference between the groups) when p < α.
With smaller samples, we can obtain an exact p-value since there is a relatively small number of possible permutations and so we can simply use F0, …, Fh where h is the number of possible permutations (or h+1 when the original order is included).
Distance metric
Until now, we haven’t defined what we mean by distance dij. There are a number of viable options, but the most common distance measurement is Euclidean distance. Let Y = [yir] be an N × k matrix.
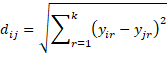
Reference
Anderson, M. J. (2005) PERMANOVA
https://pdfs.semanticscholar.org/4d0c/430f6129b427e48fb407e59ac79ee29b4cae.pdf