MANOVA Follow up using Contrasts

Univariate case

Univariate contrasts

As we describe in Planned Comparisons, for a sample with m groups, contrasts are linear combinations of the group means \sum_j c_j \mu_j based on contrast coefficients (i.e. weights) cj such that \sum_j c_j = 0. Hypothesis testing using contrasts consists of using a null hypothesis in the form of  \sum_j c_j \mu_j = 0 based on the appropriate values of the contrast coefficients as weights.

As usual we use \sum_j c_j \bar{x}_j as an estimate for \sum_j c_j \mu_j, and note that \sum_j c_j \bar{x}_j is a random variable with zero mean and variance MSW \sum_j \frac{c_j^2}{n_j}. Thus, when the null hypothesis is true the test statistic

image9144

has distribution T(dfW ). Since t ~ T(df) is equivalent to t2 ~ F(1, df), it follows that this test is equivalent to

image9145

Orthogonal contrasts

Contrasts \sum_j c_j \bar{x}_j and \sum_j d_j \bar{x}_j are orthogonal provided \sum_j \frac{c_j d_j}{n_j} = 0, which in the balanced case, where n1 = n2 = ⋯ = nm, is the same as stating that the vectors (c1, …, cm) and (d1, …, dm) are orthogonal.

Note that the null hypotheses of orthogonal contrasts are independent of one another; i.e. the result of one has no impact on the result of the other.

If ψ1, …, ψm-1 are m –1 contrasts that are pairwise orthogonal, then any other contrast can be expressed as a linear combination of these contrasts. Thus you only ever need to look at m – 1 orthogonal contrasts. Since \sum_{j=1}^m c_j = 0 for any contrast, each of the ψj is orthogonal to the unit vector (1, …, 1) and so m –1 contrasts (and not m) are sufficient. Also by Corollary 1 of Orthogonal Vectors and Matrices, we can always find a set of m –1 contrasts.

Note that if ψ1, …, ψm-1 are pairwise orthogonal contrasts, then SS between groups, SSB = SS_{\psi_1} + ⋯ + SS_{\psi_{m-1}}. Also each df_{\psi_j} = 1, and so m – 1 = df_{\psi_1} + ⋯ + df_{\psi_{m-1}}. Thus any m – 1 pairwise orthogonal contrasts partition SSB.

Multivariate contrasts

Multivariate contrasts are linear combinations of the group mean vectors \sum_j c_j \mu_j based on contrast coefficients (i.e. weights) cj such that \sum_j c_j = 0. Hypothesis testing using contrasts consists of using a null hypothesis in the form of  \sum_j c_j \mu_j = 0 based on the appropriate values of the contrast coefficients as weights.

As usual we use \sum_j c_j \bar{X}_j as an estimate for \sum_j c_j \mu_j, and note that \sum_j c_j \bar{X}_j is a random vector with zero mean and covariance matrix 

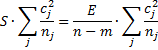
image9146

Multivariate orthogonal contrasts

Contrasts \sum_j c_j \bar{X}_j and \sum_j d_j \bar{X}_j are orthogonal provided \sum_j \frac{c_j d_j}{n_j} = 0, which in the balanced case, where n1 = n2 = ⋯ = nm, is the same as stating that the vectors (c1, …, cm) and (d1, …, dm) are orthogonal.

Note that the null hypotheses of orthogonal contrasts are independent of one another; i.e. the result of one has no impact on the result of the other.

If ψ1, …, ψm-1 are m –1 contrasts that are pairwise orthogonal, then any other contrast can be expressed as a linear combination of these contrasts. Thus you only ever need to look at m – 1 orthogonal contrasts. Since \sum_{j=1}^m c_j = 0 for any contrast, each of the ψj is orthogonal to the unit vector (1, …, 1) and so m – 1 contrasts (and not m) are sufficient. Also by Corollary 1 of Orthogonal Vectors and Matrices, we can always find a set of m – 1 contrasts.

Hypothesis matrix

Let ψ = \sum_j c_j \bar{X}_j be a contrast. Then we can define the hypothesis SSCP matrix for ψ as follows:

image9147

Note that if ψ1, …, ψm-1 are pairwise orthogonal contrasts, then the hypothesis matrix H can be partitioned H = H_{\psi_1} + ⋯ + H_{\psi_{m-1}}. Also each df_{\psi_j} = 1, and so m – 1 = df_{\psi_1} + ⋯ + df_{\psi_{m-1}}.

Since in our representation of the data we exchange the roles of rows and columns and represent contrasts as column vectors, we actually calculate

image9148

Hypothesis testing

The test we use to determine whether to retain or reject the null hypothesis is similar to the omnibus MANOVA test and uses the test statistic

Wilk’s Lambda: Λψ = \frac{|E|}{|H_\psi+E|}

For the Wilks Lambda test, we use df1 = k and b = 1 and so the test becomes

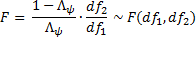image9149where df1 = k and df2 = n – m – k + 1.

Example

Example 1: We have seen that there are significant differences between the four groups in Example 1 of Manova Basic Concepts, but we still don’t know where these differences are. Based on the observations we made when looking at the charts in Figure 3 of Manova Basic Concepts, we would like to answer the following questions:

  1. Is there a significant difference between the clay and salty groups?
  2. Is there a significant difference between the loam and sandy groups?
  3. Do the loam/sandy groups have a higher mean vector than the clay/salty groups?

Question (a)

To answer the first question we select the Contrasts option in the Real Statistics MANOVA data analysis tool (see Figure 1 of Real Statistics Manova Support). The result is as shown in Figure 1.

Manova contrast blank Excel

Figure 1 – Contrasts option of MANOVA data analysis tool

Don’t worry about the #DIV/0! And zero entries. Remember we still haven’t filled in the contrast coefficients in the shaded area.

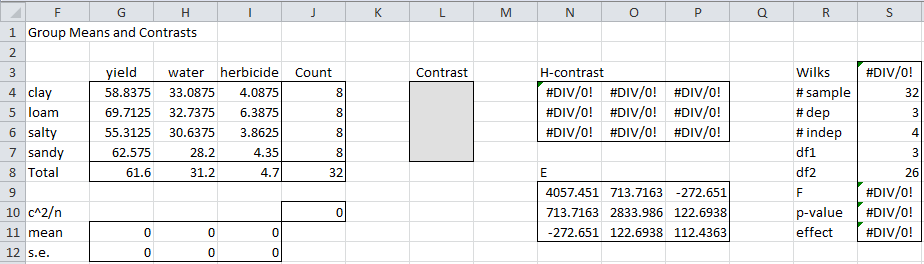
For question (a), we use the following coefficients: 1 for clay, -1 for salty and 0 for loam and sandy. The results are shown in the top half of Figure 2.

Manova contrasts Excel

Figure 2 – Contrasts for questions (a) and (b)

This time we get non-error values for all the cells. Key formulas used to create the contrast table in Figure 2 are given in Figure 3.

manova-contrasts-formulas-excel

Figure 3 – Representative formulas from Figure 2

The p-value (cell S10) = 0.896 > .05 = α, and so there is no significant difference between the mean vectors of the clay and salty groups.

Question (b)

For question (b) we can again select the Contrasts option in the Real Statistics MANOVA data analysis tool and enter the contrast with coefficients 1 for loam, -1 for sandy and 0 for clay and salty. Alternatively, you can simply copy the output for the contrast for question (a) right below it (as in the bottom part of Figure 2) and simply change the contrast coefficients. As we can see from Figure 2, the p-value for question (b) is .060268, which is again larger than α = .05, and so we conclude there is no significant difference between the mean vectors of the loam and sandy groups.

Question (c)

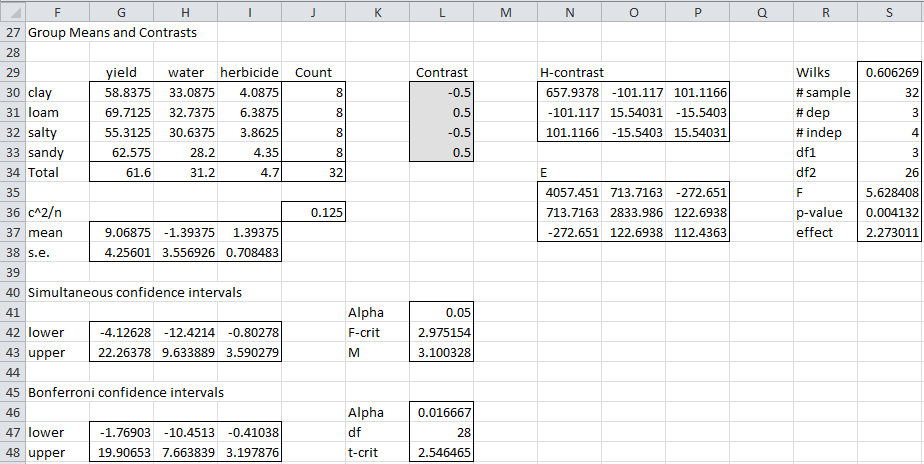
For question (c) we use contrasts 1/2 for loam and sandy and -1/2 for clay and salty. This time, as we see in Figure 4, we get a p-value of .004132 < .05 = α, which shows there is a significant difference between the mean vectors.

Manova contrast data analysis

Figure 4 – Contrasts for question (c)

Observation: It turns out that the three contrasts evaluated above are mutually orthogonal. You don’t necessarily have to use only orthogonal contrasts. In fact, it is best to use the contrasts that correspond to the tests that you believe are necessary to perform based on the actual experiment under consideration.

Simultaneous confidence intervals

Example 2: We have seen that the loam/sandy groups have a significantly higher mean vector than the clay/salty groups. Which of the factors (yield, water and herbicide) account for this difference?

When we ran the Contrasts option of MANOVA for Example 1, we saw that there were two other tests conducted for question (c), as shown in Figure 4, namely the simultaneous confidence intervals and the Bonferroni confidence intervals. These two tests were also produced for questions (a) and (b), but we didn’t show the results since there weren’t significant differences in the mean vectors and so these tests were not useful.

The two tests are extensions of the same follow-up tests conducted for Hotelling’s T2 tests as described in Hotelling’s T-square Tests. We now describe the MANOVA version of these tests.

For each p, 1 ≤ p ≤ k

image9150

The 1 – α simultaneous confidence interval is

image9151

where E = [epq]

image9152

image9153

Here Fcrit = F.INV.RT(α, df1, df2), df1 = k and df2 = n – m – k + 1.

The results (see range G42:I43 of Figure 4) show that zero lies in the confidence interval for all three dependent variables, and so no one of the dependent variables accounts for the difference in mean vectors observed in Example 1(c), but it is the combination of the dependent variables.

Bonferroni confidence intervals

Generally, we use the Bonferroni confidence intervals instead of the simultaneous confidence intervals since the intervals tend to be narrower. The 1 – α Bonferroni confidence interval is

 ψp ± tcrit ∙ sep

where the contrast mean for the pth dependent variable ψp and standard error sep are as defined above and tcrit = T.INV.2T(α/k, df) where df = n – m.

The results (see range G47:I48 of Figure 4) show that although the Bonferroni confidence intervals are indeed narrower than the simultaneous confidence intervals, zero still lies in the confidence interval for all three dependent variables, and so no one of the independent variables accounts for the difference in mean vectors observed in Example 1(c), but it is the combination of the independent variables.

Effect size

We use the following value for the Mahalanobis distance squared as a measure of effect size for the multivariate contrast ψ:

image9154

For example, the effect size for Example 1(a) is 0.16071 (cell S11 in Figure 3).

The usual Cohen’s default interpretation of Dψ (i.e. the square root of the above measure) is .20 (small), .50 (medium) and .80 (large). Thus for Example 1(a), Dψ = .40, which is a little less than a medium effect.

Reference

Hahs-Vaghn, D. L. (2017) Applied multivariate statistical concepts. Routledge
https://books.google.it/books/about/Applied_Multivariate_Statistical_Concept.html?id=bJ6iDQAAQBAJ&redir_esc=y

26 thoughts on “MANOVA Follow up using Contrasts”

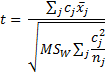
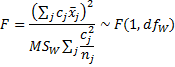
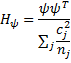
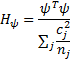
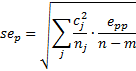
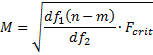
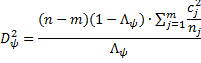
  1. Hi Charles,

    I can’t see my previous comment, trying again…

    After ANOVA you run a pairwise t-test or Tukey HSD.
    Why for MAONVA the common method, is not pairwise Hotelling T squared, or just pairwise MANOVA with two groups?
    Is a contrast test with [1,-1,0,0,0] better than MANOVA with two groups?

    Why is LDA more common?

    Thanks,

    Reply

    • Hi Benj,
      Your comment hadn’t appeared since I hadn’t had time yet to approve it for viewing by the general public.
      It should now appear and I will respond shortly.
      Charles

      Reply

  2. Dear Charles,

    Why pairwise multiple comparisons is not the common procedure for MANOVA post hoc, like for ANOVA?
    comparing every combination of groups using Hotelling’s T-square, or better MANOVA with two groups with the preferred statistic? I assume Pillai’s trace is usually the best.

    Is contrasts test with [1, -1, 0, 0 ,0] better than MANOVA(group1, group2)?

    Why LDT is better?

    Reply

    • Hello Benj,
      1. Pairwise comparisons can be used, but you need to take care of familywise error. This may result in very alpha values, making it difficult to detect a significant effect. There doesn’t seem to be a Tukey’s HSD for MANOVA, although probably discrimination analysis plays this role.
      2. Which contrast to use depends on what follow-up test you plan to use. Usually, you should plan which contrast(s) to use before you start your analysis.
      3. LDA is commonly the recommended follow-up after MANOVA. See
      https://stats.stackexchange.com/questions/111044/post-hoc-tests-for-manova-univariate-anovas-or-discriminant-analysis
      https://pjbartlein.github.io/GeogDataAnalysis/lec17.html
      Charles

      Reply

      • Thank you Charles 🙂
        You have the best statistics website.

        2. I meant to ask if pairwise contrast, is better than pairwise MANOVA two groups.
        running [1,-1,0,0], [1,0,-1,0], [1,0,0,-1] …etc, instead of:
        MANOVA(Group1, Group2), MANOVA(Group1, Group3), MANOVA(Group1,Group4) etc ?

        3. So running pairwise discrimination analysis?
        LDA finds the best discrimination axis, but is the decision, equal or not equal, only graphical? or is there any test? or agreed probability?

        Reply

        • Hello Benj,
          Sorry for the delayed response, but I have been out sick.
          2. I don’t fully understand your notation. What does [1,-1,0,0] refer to? What does MANOVA(Group1, Group2) refer to? In particular, are you referring to the independent variables (groups?) or dependent variables?
          Charles

          Reply

          • Dear Charls,

            I hope you feel better.
            I’m sorry I wasn’t clear.

            Group – one value of the independent variable.
            in your example: group1=”clay”, group2=”loam”, group3=”salty”, gorup4=”sandy”

            [1,-1,0,0] – contrast vector that compare group1=”clay” with group2=”loam”

            MANOVA(Group1, Group2) – running MANOVA only on Clay and Loam.

            2. Is pairwise contrast than pairwise MANOVA two groups?

            3. How do you use pairwise LDA? is there a decision test?

            Thanks 🙂

          • Hello Benj,
            I am feeling much better. Thank you.
            1. I don’t know which is better. In general, it is probably better to choose the version that has the smaller confidence interval. It is important that whatever groups you choose to compare, you need to choose them before collecting data and performing the omnibus MANOVA. Otherwise, you need to compare all the groups.
            2. I don’t know of Tukey’s HSD for MANOVA
            3. I don’t know of a test beyond what is already described on the website.
            Charles

  3. Charles,
    I see how you found that there is a significant difference between the loam/sandy groups and the clay/salty groups, but how can one then determine which combination has a higher mean vector? I attempted to determine this by normalizing the variables (dividing each combination mean by the total mean) and found that the sums for the three variables were higher for loam&sandy (3.20) compared to clay&salty (2.80). Is this this right method? Thanks.

    Reply

      • Charles,
        Let’s say I want to decide where to grow the new corn by maximizing yield while minimizing water and herbicide use. In order to do this and give equal weight to the three variables I think I would need to transform the data by:
        1) change the sign of water and herbicide
        2) normalize by dividing by the mean of each variable.
        Thus using the data in Fig. 1 (manova-basic-concepts) the first row would be “loam 1.24 -0.95 -1.61”. After running the MANOVA and setting the contrasts for clay&salty versus loam&sandy, the p is still 0.004, as in Fig. 4. The sum of variable averages is -1.89 for clay&salty and -2.11 for loam&sandy. Because the larger (or less negative) sum indicates a significantly better soil, I would plant the corn in a clay&salty location.
        Thanks for your feedback.

        Reply

        • Hello Dave,
          I am having trouble figuring out why this approach should determine the field to grow new corn by maximizing yield while minimizing water and herbicide. Can you explain this?
          Charles

          Reply

      • Hi Charles,

        I cannot see my previous comment here!?
        My new question is why not use Tukey HSD test to determine which of the factors (yield, water and herbicide) account for this difference?
        Thx.

        Reply

        • Hi Hamadi,
          You should be able to see your comment now. I will respond shortly.
          Tukey HSD assumes the variables are independent, which is not the case for this MANOVA example.
          Charles

          Reply

          • Hello Hamadi,
            Thank you very much for your comments. You helped me improve this webpage greatly.
            I no longer see your original comment and so I will reply to this comment.
            1. “loam/sandy groups have a significantly HIGHER mean vector than the clay/salty groups”
            This is incorrect. There is a significant difference between the vectors, but I can’t say that one is higher than the other. I have corrected this on the webpage.
            2. “Is there a typo error in the sentence (2nd ‘independent’)”
            Yes, this should be dependent. I have corrected this on the webpage.
            3. See response to comment #1.
            4. “How should the effect size be interpreted (weak, moderate, large, very large)?”
            I have added a discussion of this to the webpage.
            Charles

  4. Hello Charles,

    I think I have detected a little error in the explanation (I am not sure). In the last paragraph near the section Effect size:
    – The results (see range A40:L43 of Figure 4)
    – The results (see range A45:L48 of Figure 4)
    I think the ranges are F40:L43 and F45:L48

    Reply

    • I have just understand how the contrast work. You only have to introduce 1 and -1 one if you are comparing two groups and 0,5 and -0,5 if you are comparing 2 vs 2 groups… It is correct? I do not understand this paragraph:

      Observation: It turns out that the three contrasts evaluated above are mutually orthogonal. You don’t necessarily have to use only orthogonal contrasts. In fact, it is best to use the contrasts that correspond to the tests that you believe are necessary to perform based on the actual experiment under consideration.

      So it is always better to use MANOVA follow up using contrast than MANOVA follow up using ANOVA? Or there is any situation where it is better to use follow up using ANOVA?

      Thanks,

      Gabriel

      Thanks a lot. I think that thanks to your webpage and to your help I am near to perform the test that I want.

      Best regards,

      Gabriel

      Reply

      • In another page of the web I have mention that I have obtain an F value negative in the Multiples ANOVAs of the MANOVA. Now I know that it is because I have some missing values so it is solved. It is impossible to have an negative F value.

        About planned contrast… If I have four groups and I want to compare groups 1,2 and 3 to group 4 what numbers I should use in the grey cells? 1,1,1 and -1? And what if I want to compare groups 1 and 2 to group 3?

        Reply

        • Hello Gabriel,
          1. Yes, F should not be negative, although keep in mind that sometimes with values very close to zero Excel may produce a negative value such as -1.3E-15 (due to round off errors). This value should simply be treated as zero.
          2. For the first case, use contrasts of 1/3, 1/3, 1/3, -1 (the values should sum to zero; also you will need to enter 1/3 as =1/3). This compares group 4 with the mean of the other 3 groups.
          3. For the second case, use -.5, -.5, 1, 0. Alternatively, you can use .5, .5, -1, 0.
          Charles

          Reply

          • Thanks very much for all your replys in this page and in the rest. I really appreciate your help. What do you think of doing the MANOVA of the z-scores? Maybe in that way the covariances are homogeneous… It is a valid approach? I have read about it in this page:
            https://www.researchgate.net/post/What_s_the_nonparametric_equivalent_to_one-way_MANOVA

            In the case I use z-scores I should normalize with the standard deviation of each subject (each one perform more than one stroke), with the standard deviation of the variable in the stroke (for example having into account all the means for the stroke x), or with the total sample?

            Thanks,

            Gabriel

          • Hi Gabriel,
            You can perform MANOVA on any transformation, including the one that you are suggesting. But the real question in this case is how you will interpret the results.
            I have not familiar with the referenced paper, and so I can’t comment on it. Thanks for sending it to me since it looks interesting and eventually I plan to read it.
            Charles

  5. Hello Charles, and thank you, this is very helpful!

    I have a bit of an exceptional case with my data. I am investigating the use of various policy instruments by municipalities based on a survey they answered. I divided them between 3 size categories (SMALL, MEDIUM and LARGE). The dependent variables are “Number of instruments currently used”, “Nbr. of inst. used in the past”, “Nbr. of inst. planned for future implementation”, “Nbr. of inst. never considered for implementation” and “Nbr. of inst. where the respondent didn’t answer”.

    My issue is that “Nbr. of inst. used in the past” is equal to zero for the SMALL and MEDIUM categories. This causes Wilk’s Lambda to be either >1 or induces a division by zero when I use Real Statistics. Would you know a way around this?

    Again, thank you! My statistics are very rusty and your website has been of great help.

    Reply

  6. Dear Dr. Charles Zaiontz, thanks for answering my question.
    However the contrasts that I suggest do not produce the same simultaneous confidence intervals and, probably, are incorrect. In fact the sum of positive contrasts must be equal to +1, while the sum of negative contrasts must be equal to -1, just as you say.
    I was not aware of this rule!
    Congratulations again for your program.

    Roberto Mioni.

    Reply

  7. Dear Dr. Charles Zaiontz, I am a physician practicing in Udine (Italy). I am studying the statistics by utilizing your very interesting program “Real Statistics Using Excel”. In “MANOVA follow up using Contrasts” and in “Simultaneous confidence intervals”, you suggest to use the contrast [-0.5 0.5 -0.5 0.5] to calculate the “p – standard error”, sep.
    If I use the contrast [1 -1 -1 1], while I get the same Wilk’s Lambda and the same F – value (0.606269 and 5.628408, respectively), the “Simultaneous confidence intervals” values, [-4.126 – +22.264; -12.421 – +9.634; -0.803 – +3.590], double: [-8.2526 – +44.5276; -24.8428 – +19.2678; -1.6056 – 7.181]. Why should I use [-0.5 0.5 -0.5 0.5] contrasts and not [-1 1 -1 1]?
    Best regards, Roberto Mioni.

    Reply

    • Roberto,
      I typically choose contrasts such that the sum of the negative contrasts equals -1 and the sum of the positive contrasts equals +1. The contrasts that you suggest will probably produce the same outcome.
      Charles

      Reply

Leave a Comment