Univariate case
As described in One Sample t-Test, the t-test can be used to test the null hypothesis that the population mean of a random variable x has a certain value, i.e. H0: μ = μ0. The test statistic is given by
The applicable univariate test of the null hypothesis is based on the fact that t ~ T(n–1) provided the following assumptions are met:
- The population of x has a unique mean: i.e. there are no distinct sub-populations with different means
- The population of x has a normal distribution
- The data consists of a random sample with each element in the sample taken independently
Regarding the normality assumption, if n is sufficiently large, the Central Limit Theorem holds. In this case, we can proceed as if the population were normal. It turns out that the t-test is pretty robust to violations of the normality assumption provided the population is relatively symmetric about the mean.
The null hypothesis is rejected if |t| > tcrit. Also, by Property 1 of F Distribution, an equivalent test can be made using the test statistic t2 and noting that t2 ~ F(1, n – 1).
Now, t2 can be expressed as follows:
where x̄ is the sample mean and s is the sample standard deviation.
Multivariate case
Experiment-wise error
We now look at a multivariate version of the t-test, which decides whether the population mean of the k × 1 random vector X has a certain value. Here, the null hypothesis is H0: μ = μ0 where μ and μ0 are vectors.
Since the null hypothesis is true when μi = μi0 for all i, 1 ≤ i ≤ k, one way to carry out this test is to perform k separate univariate t-tests (or the equivalent F tests). The null hypothesis is then rejected if any one of these k univariate tests rejects its null hypothesis.
As we observed in Experiment-wise Error Rate, this approach introduces experiment-wise error, namely, if we use a given value of α for all k tests, then the probability of the multivariate null hypothesis being rejected is much higher than α. For this reason, we typically use a correction factor, usually, the Dunn/Sidák or Bonferroni correction factor, as described in Planned Comparisons. Thus, we use a significance level of 1 –(1–α)1/k or α/k instead of α for each of the k univariate tests.
This approach is perfectly reasonable when the random variables xi in X are independent. But when they are not independent then the Dunn/Sidák or Bonferroni correction factors over-correct and the resulting experiment-wise value for α is lower than it needs to be, which results in a test with lower statistical power.
Since it is common to create experiments in which the random variables xi in X are not independent, it is better to use a different approach. In particular, we will use the multivariate test based on Hotelling’s T-square test statistic.
T-square statistic
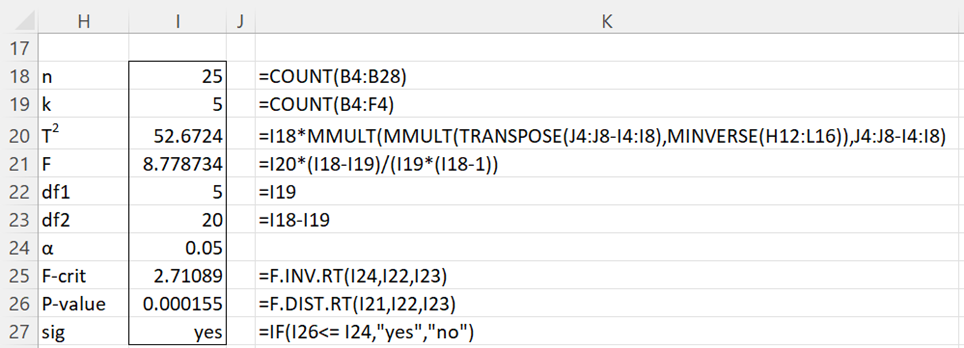
Definition 1: Hotelling’s T-square test statistic is
where S is the covariance matrix of the sample for X, X̄ is the mean of the sample, and the sample has n elements.
Note the similarity between the expression for T2 and the expression for t2 given above.
Property 1:
Corollary 1: By the multivariate version of the Central Limit Theorem, for n sufficiently large, T2 ~ χ2 (k).
For small n, Property 1 doesn’t yield results that are sufficiently accurate. A better estimate is achieved using the following property.
Property 2: Under the null hypothesis
If F > Fcrit then we reject the null hypothesis.
Example
Example 1: A shoe company evaluates new shoe models based on five criteria: style, comfort, stability cushioning, and durability. Each of the first four criteria is evaluated on a scale of 1 to 20 and the durability criterion is evaluated on a scale of 1 to 10. Column I of Figure 1 shows the goals for each criterion expected from new products.
Figure 1 – Product goals by criteria
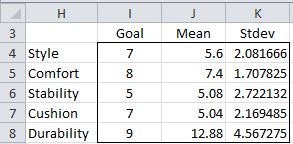
Based on the evaluations of 25 people about the company’s latest prototype (Model 1) shown in Figure 2, determine whether the shoe is ready for release to the market.
Figure 2 – Sample data for Example 1
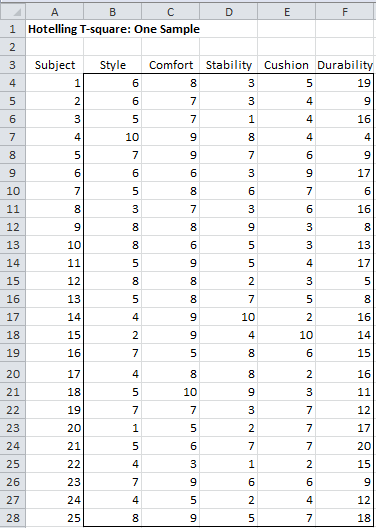
The sample mean and standard deviation for each criterion are shown in columns J and K of Figure 1. The sample covariance and correlation matrices are then calculated using the Real Statistics array formulas COV(B4:F28) and CORR(B4:F28), as shown in Figure 3.
Figure 3 – Covariance and Correlation Matrices
Results
Using Definition 1 and the data in Figures 1, 2, and 3, we can calculate T2 as shown in cell I20 of Figure 4. Since the formula used to calculate T2 is an array formula (even though it yields a scalar numeric result), it is important to press Ctrl-Shft-Enter after entering the formula in cell I20 (unless using Excel 365 where this is not necessary).
Figure 4 – Hotelling T2 test for a single sample
As we will see shortly, you can also obtain T2 by using the formula
=HotellingT2(B4:F28,I4:I8)
which employs the Real Statistics function HotellingT2 found in the Real Statistics Resource Pack. Since this formula is not an array formula, it is sufficient to press Enter after entering the formula.
We can determine whether there is a significant difference between the sample means in the five categories and the goals (i.e. population means) by using Property 2. As can be seen from Figure 4, since p-value < .05 (or F > Fcrit), we reject the null hypothesis and conclude there is a significant difference between the mean scores in the sample and the stated goals.
Confidence intervals
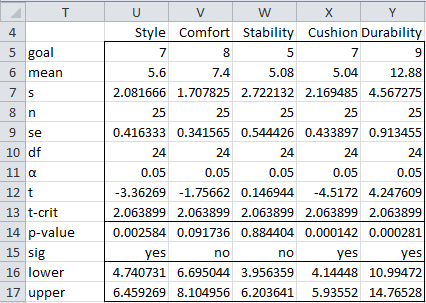
Example 2: For the prototype shoe in Example 1, determine which criteria meet the goals and which do not.
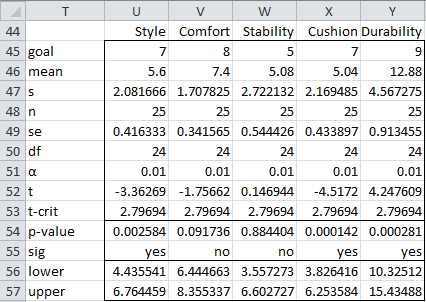
We can test each criterion using a One Sample t-Test. The results of this analysis are shown in Figure 5.
Figure 5 – T-test for each criterion
From Figure 5, we can conclude that Style and Cushioning are significantly below the goals. Durability is significantly higher than the goals and Comfort and Stability are within the goals.
Figure 5 includes the 95% confidence intervals for each criterion. In the univariate case, the 1–α confidence interval for the population mean μ is based on
which nets out to the interior of the interval
The problem with this analysis is that we haven’t taken experiment-wise error into account. In fact, the combined (worst-case) error rate is 1-(1-.05)5 = .226 instead of .05.
If the random variables representing the 5 criteria were independent, then we could compensate for this by applying either the Dunn/Sidák or Bonferroni correction factor. As we can see from the correlation matrix in Figure 2, the variables are clearly not independent since some of the values off of the main diagonal are far from zero.
Simultaneous intervals
In order to control for experiment-wise error, we instead calculate the 95% confidence ellipse (using Property 2) which takes all 5 criteria into account simultaneously. In particular, we use the following modified version of the observation which follows Property 3 of Multivariate Normal Distribution Basic Concepts, noting that based on Definition 1 and Definition 3 of Multivariate Normal Distribution Basic Concepts, T2 is approximately n times the Mahalanobis distance between X-bar and μ0.
Using Property 2, we have a 1 – α confidence hyper-ellipse for the population mean vector μ which is given by
Thus, we are looking for values of μ which fall within the hyper-ellipse given by the equation
From the 1–α confidence hyper-ellipse, we can also calculate simultaneous confidence intervals for any linear combination of the means of the individual random variables. For example, for the linear combination
the 1 – α simultaneous confidence interval is given by the expression
where the sample covariance matrix is S = [sij].
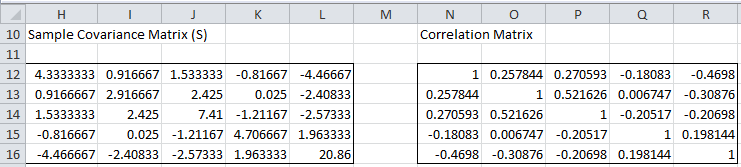
For the case where c = μi the 1–α simultaneous confidence interval is given by the expression
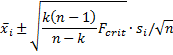 where si is sii = the standard deviation of the xi.
where si is sii = the standard deviation of the xi.
Example
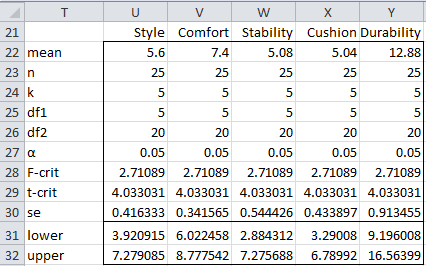
Since the 1–α confidence intervals for all linear combinations are a manifestation of the 1–α confidence hyper-ellipse, it follows that the simultaneous 95% confidence intervals for all 5 criteria are as shown in Figure 6.
Figure 6 – Simultaneous 95% confidence intervals
Most of the cells in Figure 6 already appear in Figure 4. The value of t-crit (e.g. cell U29) is derived from F-crit using the formula =SQRT(U24*(U23-1)/(U23-U24)*U28). The value of the lower bound of the 95% confidence interval for Style is calculated by the formula =U22-U29*U30, and similarly for the upper and lower bounds of the other criteria.
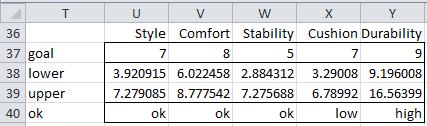
We summarize the conclusions from this analysis in Figure 7.
Figure 7 – Comparison of simultaneous intervals with goals
From Figure 7, we conclude that Cushioning is significantly below the goals, Durability is significantly higher than the goals and the other criteria are within the goals set by the company.
Bonferroni intervals
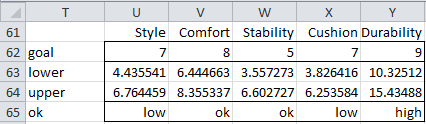
The simultaneous confidence intervals handle all linear combinations of the means, but since we are only interested in the individual means, the stated confidence intervals may be too wide. In this case, we might be better off using the Dunn/Sidák or Bonferroni correction factor. The calculations for the Bonferroni correction factor are similar to those in Figure 5, except that we use the experiment-wise value of alpha = α/k = .05/5 = .01. The results are shown in Figure 8.
Figure 8 – Bonferroni confidence intervals
The confidence intervals in Figure 8 are narrower than those in Figure 7. Also, the overall conclusions are a little different, as shown in Figure 9.
Figure 9 – Comparison of Bonferroni intervals with goals
Although we will generally use the hyper-ellipse based on F as described above, for large samples, based on Corollary 1, we could also use the following 1–α confidence hyper-ellipse for any linear combination c of the means:
Where c = μi, this nets out to
![]()
Effect Size and Power
Click here for two measures of effect size for the one-sample Hotelling’s T-square test as well as how to calculate the power of this test.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Penn State University (2013) Hotelling’s T-square. STAT 505: Applied multivariate statistical analysis (course notes)
https://online.stat.psu.edu/stat505/lesson/7/7.1/7.1.3
Rencher, A.C. (2002) Methods of multivariate analysis (2nd Ed). Wiley-Interscience, New York.
http://math.bme.hu/~csicsman/oktatas/statprog/gyak/SAS/eng/Statistics%20eBook%20-%20Methods%20of%20Multivariate%20Analysis%20-%202nd%20Ed%20Wiley%202002%20-%20(By%20Laxxuss).pdf
Johnson, R. A. and Wichern, D. W. (2007) Applied multivariate statistical analysis. 6th Ed. Pearson.
https://mathematics.foi.hr/Applied%20Multivariate%20Statistical%20Analysis%20by%20Johnson%20and%20Wichern.pdf
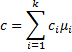
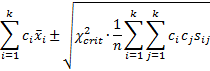
Hi charles,
Thanks for the detailed contents on t-test using excel. Doing it in excel is helpful to improve method understanding.
I would want to know more about following statements,
“The applicable univariate test of the null hypothesis is based on the fact that t ~ T(n – 1)…………
…. The null hypothesis is rejected if |t| > tcrit. Also note that by Property 1 of F Distribution, an equivalent test can be made using the test statistic t2 and noting that t2 ~ F(1, n – 1).”
t is calculated or scored t value, based on data and T(n-1) is critical t-value/t-critical.
so, if scored t-value is less than or equal to t-critical, conclusion would be, we fail to reject null hypothesis. Similarly, can be concluded for t2 statistics.
I am trying to understanding why do we say “null hypothesis is based on the fact that t ~ T(n – 1)” or “null hypothesis is based on the fact that t2 ~ F(1, n – 1)”.
Thanks in advance.
Appreciate your efforts to real statistic’s using excel.
For t ~ T(n – 1), see
Property 1 of https://www.real-statistics.com/students-t-distribution/t-distribution-basic-concepts/
https://www.real-statistics.com/students-t-distribution/one-sample-t-test/
For t2 ~ F(1, n – 1), see
Property 1 of https://www.real-statistics.com/chi-square-and-f-distributions/f-distribution/
Charles
Hello,
I keep getting an error on the one sample test that the object variable or with block variable not set
Hello Peter,
If you email an Excel file with your data, I wiull try to figure out what is going wrong.
Charles
Dr. Zaiontz
I was experimenting with you RealStat Add-In to perform a One Sample Hotelling’s T-square test and then needed to calculate confidence intervals (simultaneous intervals and Bonferroni confidence intervals) . While I can do them by hand in excel your web site alludes to the fact that the Add-In can perform this using the One Sample t-Test, but I don’t fined that option in the Add-In.
PS. Really appreciate your work
Jeff,
The one-sample t test is an option on the T Test and Nonparametric Equivalents data analysis tool.
Charles
Dear Charles,
I created 10 small samples (500 instances) from a large dataset.
I wish to perform Hotelling’s T-squared test to check if my samples are representatives of the original dataset. Could I do two-sample test or do I need to perform one-sample test instead? Thank you
Nush,
I don’t understand why you would want to do such a thing if you know that these are random samples from the large data set. Also why do you want to use Hotelling’s T-square test to do this?
Charles
Dear Charles,
This dataset contains 60 features. Therefore, I need to perform a mutivariate analysis. My objective is to show that the selected random instances are of representative instances of the original dataset.
Thank you.
I have a question please.
In a case where 7 human subjects were given an alcoholic drink and blood samples for glucose concentration for each sample, were taken from the 7 subjects at 1,2,3 &4 hrs intervals after the consumption of the alcoholic drink. If we intend to test whether blood glucose concentrations are the same for the four time points, what test statistics can I use?
Anie,
You can use repeated measures ANOVA or repeated measures MANOVA.
Charles
Hey Charles, I need your help for my final project.
the project data has 552 data points with each data record containing 209 values.
I need to perform phase 1 analysis, eliminate the Out of control points, determine the statistical parameters and then perform a Principal component analysis.
How can you help me in this?
Hi Nathan,
Please start by looking at the Factor Analysis webpages. See
Factor Analysis
Charles
One other question – do you know the convention for reporting results of Hotelling’s T2 test? Do you report the T2 statistic or the F value?
I don’t know the convention, but based on how these tests are usually reported, you should report both the T2 statistic and the F value.
Charles
That makes sense. Thank you!
I am learning a great deal on this site that is helpful for my current research. Another question I am wondering about is as follows:
From what I understand, Hotelling’s T2 statistics will tell me if a linear composite of the different components differs from the constant (or goal). Suppose I am interested in an overall directional hypothesis, wondering if the components are not just different from the constant, but different in a specific direction.
Take your shoe company data as an example (and suppose that the goals for each of the categories was the same – 7 out of 10). What if I wanted a multivariate statistic to tell me whether, on average across categories, our shoe performs better than 7. Is there a multivariate test for that? Or would I simply take the overall mean across all categories, and conduct a univariate t-test?
I apologize for monopolizing this page, but this information has been profound helpful to me, and I thank you for it. If you have opportunity to respond, please do.
Thanks again!
Chris
Chris,
Perhaps I am not interpreting your question properly, but I would think the answer is no, since I tend to think of these linear composites as vectors and so the likelihood is that two vectors intersect and so one is not larger than the other. This is my initial intuition, but perhaps someone in the community has a different idea.
Charles
Charles – I am running through your example, and am running into an issue. When I input the covariance statement “=COV(B4:F28)”, it only returns one cell (4.3333) instead of the matrix you have in Figure 3. Is there something I am missing? (I am using Excel 2011 for Mac.)
Thanks for this great resource!
Nevermind – I figured it out. But for any other Mac users out there, it required highlighting the 5×5 cell range for the output and clicking Command+Shift+Enter (instead of Ctrl+Shift+Enter in Windows).
I rewrite this in C++.
https://github.com/niitsuma/hotelling_t_square_test
May I use example data as test data?
https://github.com/niitsuma/hotelling_t_square_test/blob/master/hotelling_t2_test.cpp
Of course I need to protect the copyright on the software and website content, but I don’t have any problem with you using the test data for the hotelling T tests from my website.
Charles