Univariate case
When the variances of the two populations are unequal (as indicated by notably unequal sample variances), we use a modified version of the t-test. In particular, we use the following t-statistic
We now test the null hypothesis H0: μx = μy using the fact that t ~ T(df) where m is defined as
(see Two Sample t Test with Unequal Variances). This is equivalent to
where t2 can be expressed as:
where z̄ = x̄ – ȳ and µz = µx – µy.
Multivariate case
We now look at a multivariate version of the problem, namely to test whether the population means of the k × 1 random vectors X and Y are equal, i.e. the null hypothesis H0: μX = μY, under the assumption that the covariance matrices are not necessarily equal.
Definitions and Properties
Definition 1: The modified two-sample Hotelling’s T-square test statistic is
Observation: Note the similarity between the expression for T2 and the expression for t2 given above. Also note that if nX = nY, then this definition of T2 is equivalent to that in Definition 1 of Hotelling’s T-square for Independent Samples.
Property 1: For nX and nY sufficiently large, T2 ~ χ2(k).
For small nX and nY, T2 is not sufficiently accurate and a better estimate is achieved using the following theorem
Property 2: Under the null hypothesis,
where n = nX + nY – 1 and m is defined as follows:
If F > Fcrit then we reject the null hypothesis.
Example
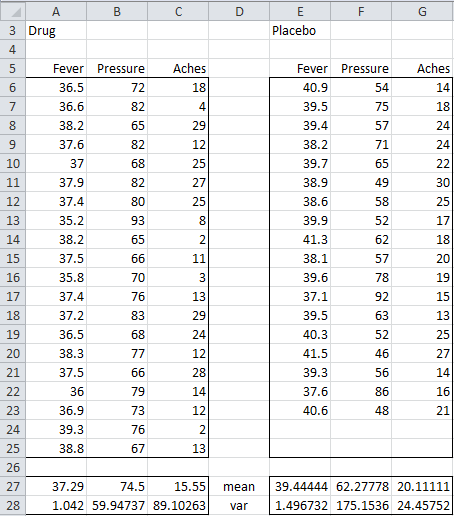
Example 1: Repeat Example 1 of Hotelling’s T-square for Independent Samples using the data in Figure 1.
Figure 1 – Data for Example 1
Once again, we employ Box’s test, obtaining the results shown in Figure 2.
Figure 2 – Box’s Test for Example 1
This time we see that p-value < α = .05, and so we conclude that there is evidence that the covariance matrices are unequal (or that the data is not multivariate normally distributed), although we have somewhat forced the issue since usually a significance level of α = .001 instead of α = .05 is used for Box’s Test.
As a result, we will use the T2 test with unequal covariance matrices. This analysis is shown in Figure 3.
Figure 3 – Analysis for Example 1
We conclude there is a significant difference between the drug and the placebo in treating the symptoms.
Confidence intervals
The simultaneous 1 – α confidence interval for μi is given by the expression
For n sufficiently large, we could use the following expression instead
Once again we can use Bonferroni confidence intervals instead. See One-sample Hotelling’s T-square Test for details.
References
Penn State University (2013) Hotelling’s T-square. STAT 505: Applied multivariate statistical analysis (course notes)
https://online.stat.psu.edu/stat505/lesson/7/7.1/7.1.3
Rencher, A.C. (2002) Methods of multivariate analysis (2nd Ed). Wiley-Interscience, New York.
https://www.ipen.br/biblioteca/slr/cel/0241
Johnson, R. A. and Wichern, D. W. (2007) Applied multivariate statistical analysis. 6th Ed. Pearson.
https://www.webpages.uidaho.edu/~stevel/519/Applied%20Multivariate%20Statistical%20Analysis%20by%20Johnson%20and%20Wichern.pdf
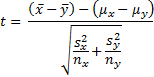
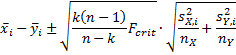
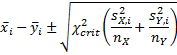
Hi Charles !
I am doing an analysis on the multivariate hotelling T square in which I am interested to study the variables ( science stream and arts stream) don’t differ significantly with semesters (I,II,III,IV,V&VI) , a graduate level exam . Is it an appropriate test for the analysis ? If yes , what type of hotelling T square should be done?
In any given semester are the same students taking the exam or different students?
Charles
Yes,all are same students taking (I to VI) the semester exams .But students are catagoriesd into samples .( science and arts)
Please I’m working on multivariate analysis on the response of crop to soil type and fertilizer how do I use manova to do this
For more information about MANOVA, see
MANOVA
Charles
Dear Prof. Charles Zaiontz,
I studied the Hotelling test in order to evaluate if a unique sample (I have just one value for each variable, so n_x=1) could belong to a population, whose I have n_y values of the different variables. In your opinion, is the Hotelling procedure with unequal covariance matrix adapt? How can I overcome to the problem of obtaining zero to the denominator (probably saying that I have 2 equal observations of the p variables)? If in your opinion this is not the right procedure, can you suggest me a more adapt one, please?
Thanks for your attention.
Best regards
Ensia,
Are you saying that your sample consists of just one element in each group? In this case, you should expect much no matter what statistical test you use.
Charles
Dear Charles,
Thank you very much for this website, it helps a ton in helping me understand Hotelling’s test.
I was wondering whether you can explain to me why Hotelling’s test uses the F distribution? I cannot seem to connect the test with the F distribution.
Thank you a lot for your help,
Lakyn
Lakyn,
To give a precise answer to your question would require the proof of Theorem 2 on the referenced webpage, which is too technical for our purposes. One way to motivate why the F distribution might be involved:
– the univariate version of the Hotelling’s test is the t-test, which uses the t distribution
– the t distibution can be expressed via the F distribution since if t has distribution T(df), then t^2 has distribution F(1,df)
Charles
Dear Charles,
Thank you for your reply!
I was just wondering where is the referenced webpage? The proof is something that I will be very interested in looking at.
Sincerely,
Lakyn
Lakyn,
The referenced webpage is simply the webpage where you made your comment (Hotelling’s T-square Test with Unequal Covariance Matrices in this case).
I believe the following website has the proof (although I have not read this article myself):
http://www.math.sci.hiroshima-u.ac.jp/stat/TR/TR12/TR12-19.pdf
Charles
This is what I was looking for. Thank You for Your work.
Charles,
I love this website. Thank you.
I’m currently dealing with a zero inflated dataset. I’m applying the Hotelling’s T2 test to these data and was wondering if there are issues with having a lot of zeros in the data.
I’m comparing two sites (control and experimental) using fish densities at 1 m depth increments (total of 15). The sample size for each 1 m depth increment is 50. So a matrix that is [50,15].
Garrett,
Thanks for letting me know that you love the website.
Regarding your question, unfortunately I don’t have any experience with Hotelling’s T2 test with zero-inflated data, and so I am not able to answer your question.
Charles