One-sample Hotelling’s T-square Test
We can calculate the power and minimum sample size in the same manner as described for the one-sample t-test based on the Mahalanobis distance effect size d and the noncentrality parameter equal to
ncp = n · d2
The power can be expressed as
1 – β = NF_DIST(fcrit, k, n-k, TRUE)
where
fcrit = F.INV.RT(α, k, n-k)
and n = the sample size and k = the number of dependent variables.
Example 1: What is the power for a one-sample Hotelling’s T-square test on a sample of size 50 with 3 dependent variables where Mahalanobis distance effect size d is .5 and α = .05?
As we can see from Figure 1, the power is 82.3%.
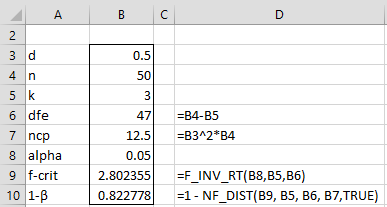
Figure 1 – Power of Hotelling’s T-square test
Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack provides the following functions.
Hotel1_POWER(d, n, k, type, alpha, iter, prec) = the statistical power for a one-sample Hotelling’s T-square test where the sample size is n, the number of dependent variables is k and the effect size is d, where d = Mahalonobis distance effect size if type = 1 (default) and d = ncp if type = 2.
Hotel1_SIZE(d, k, pow, alpha, iter, prec) = the minimum sample size to obtain statistical power of pow for one sample Hotelling’s T-square test where the number of dependent variables is k and the Mahalonobis effect size is d
alpha is the significance level (default .05). iter = the maximum number of iterations used in calculating the answer (default 1000) up to a precision of prec (default 0.000000001). The default for pow is .80.
The power for Example 1 can be calculated by =Hotel1_POWER(B3,B4,B5)
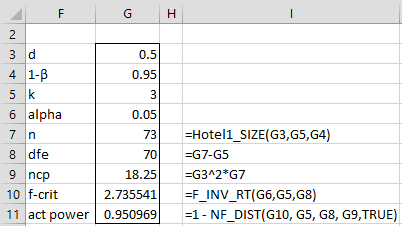
Example 2: What sample size is required to achieve 95% power for the experiment described in Example 1?
As we can see from Figure 2, a sample of size 73 is required.
Figure 2 – Sample size required for Hotelling’s T-square test
Two-sample Hotelling’s T-square test
Power and minimum sample size for a two-sample Hotelling’s T-square test can be calculated in the same manner as for a one-sample Hotelling’s T-square test, noting that in this case
ncp = n1·n2/(n1+n2) · d2 df = n1 + n2 – (k+1)
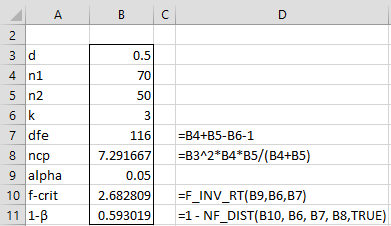
Example 3: What is the power for a two-sample Hotelling’s T-square test on samples of size 70 and 50 with 3 dependent variables where Mahalanobis distance effect size d is .5 and alpha = .05?
As we can see from Figure 3, the power is 59.3%.
Figure 3 – Power of two-sample Hotelling’s T-square test
More Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack provides the following functions.
Hotel2_POWER(d, n1, n2, k, type, alpha, iter, prec) = the statistical power for a two-sample Hotelling’s T-square test where the sample sizes are n1 and n2, the number of dependent variables is k and the effect size is d, where d = Mahalonobis distance effect size if type = 1 (default) and d = ncp if type = 2.
Hotel2_SIZE(d, k, pow, alpha, nratio, iter, prec) = the minimum sample size to obtain the statistical power of pow for a two-sample Hotelling’s T-square test where the number of dependent variables is k and the Mahalonobis distance effect size is d
alpha is the significance level (default .05), iter = the maximum number of iterations used in calculating the answer (default 1000) up to a precision of prec (default 0.000000001), and the default for pow is .80.
For Hotel2_SIZE, only the size of the first sample is returned. If you don’t want the two samples to have the same size, you can specify the size of the second sample in terms of the size of the first sample using the nratio argument. E.g. if the size of the second sample is half of the first, then set nratio = .5.
If you set nratio to be a negative number then the absolute value of this number will be used as the size of the second sample. E.g. if nratio = -50, then the Hotel2_SIZE function will find the size of the first sample assuming that the second sample has 50 elements.
The power for Example 3 can be calculated by =Hotel2_POWER(B3,B4,B5, B6).
Example
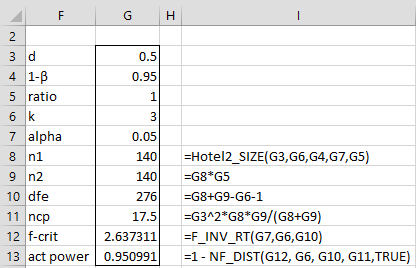
Example 4: What sample sizes are required to achieve 95% power for the experiment described in Example 3 where we assume the two samples are equal in size?
As we can see from Figure 4, samples of size at least 140 are required.
Figure 4 – Sample size for two-sample Hotelling’s T-square test
References
Hintze, J. L. (2011) Hotelling’s one-sample T-square. NCSS PASS
http://www.ncss.com/wp-content/themes/ncss/pdf/Procedures/PASS/Hotellings_One-Sample_T2.pdf
Efird, J. T. and Aliminetti, K. (2004) Computing exact power and sample size for Hotelling’s T2-test and related multivariate procedures
https://www.lexjansen.com/wuss/2004/data_analysis/c_das_computing_exact_power_.pdf