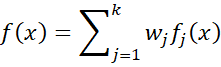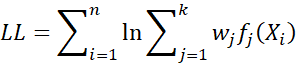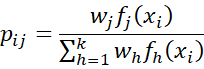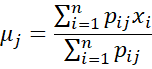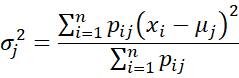Univariate GMM

Introduction

Gaussian Mixture Models (GMM) are models that represent normally distributed subpopulations where each subpopulation may have different parameters (mean and variance) and for each element in the population we don’t know a priori which subpopulation that data element belongs to.

For example, suppose that our population consists of the height of adults in the population. We can model this by a GMM with two components, corresponding to the subpopulations of men and women. E.g. suppose that men’s heights are normally distributed with mean 69.2 inches and standard deviation 1.2, while women’s heights are normally distributed with mean 63.6 and standard deviation 1.1.

In fact, the model doesn’t know in advance any of these parameters, just that there are two components and each of these subpopulations are normally distributed.

Objective

On this webpage we describe how to create a GMM model based on univariate data. We start with a sample of size n and assume that there are k subpopulations C1, …, Ck. Our objective is to estimate the parameters of the normal distribution for each of the k subpopulations (aka components). More specifically, for each i, we want to estimate μi and σi so that for a data element x in Ci, x ∼ N(μi, σi). 

We also want to determine for any x (in the sample or population) what is the probability that x belongs to subpopulation Ci for i = 1, 2, …, k. We can, if we choose, then assign x to that subpopulation with the highest probability. This is a form of cluster analysis where the Ci are the clusters. This is a type of “soft clustering” since the assignment probabilities are produced, unlike k-means clustering where only an assignment cluster is made.

Model Specification

We specify a GMM model by the following parameters:

  • k = number of components
  • wj = weight (aka the mixture coefficient) of the jth component where the sum of the weights is 1
  • μj = mean of the jth component
  • σj = standard deviation of the jth component

For each x in the population, the pdf f(x) at x is

Gaussian mixture pdf

where fj(x) is the probability density function (pdf) of a normal distribution with mean μj and standard deviation σj. This is the general format for a mixture model. Since this is Gaussian (i.e. normal distribution) mixture model, we can calculate fj(x) in Excel by

fj(x) = NORM.DIST(x, μj, σj, FALSE)

The model parameters are estimated from a sample X = x1, x2, …, xn as explained next.

Model Estimation

We estimate the model parameters μj, σj, and wj by maximizing the log-likelihood function

Log-likelihood function

We accomplish this by using the Expectation-Maximization (EM) algorithm (see EM Algorithm). This is a type of unsupervised learning, and consists of the following steps.

Step 0 (initialization)

  • Estimate wj by 1/k for each component.
  • Select k elements randomly without replacement from the X and assign these as estimates for μ1, …, μk.
  • Estimate the standard deviation σj for all j by the standard deviation of X.

There are a number of alternative approaches for initializing the μj, σj, and wj parameters, including using the results from k-means clustering.

Step m for m > 0 (EM algorithm)

We now perform a series of EM steps consisting of an E step followed by an M step. 

E step

For each i = 1, …, n and j = 1, …, k, define pij = the probability that sample element xi is in component Cj, namely

p_ij

where fh(x) is the pdf of the normal distribution with the current estimates of μh and σh.

M step

Re-estimate the model parameters as follows:

w_j

mu_j

sigma-sq_j

Termination

We repeat the EM steps until a maximum number of iterations is reached or until some sort of convergence criterion is met.

References

McGonagle, J. et al (2024) Gaussian mixture model
https://brilliant.org/wiki/gaussian-mixture-model/

Carrasco, O. C. and Whitfield, B. (2024) Gaussian mixture models explained
https://builtin.com/articles/gaussian-mixture-model

GeeksforGeeks (2023) Gaussian mixture model
https://www.geeksforgeeks.org/gaussian-mixture-model/

Apgar, V. (2023) 3 use-cases for Gaussian Mixture Models (GMM)
https://towardsdatascience.com/3-use-cases-for-gaussian-mixture-model-gmm-72951fcf8363

Leave a Comment