Principal Axis Method of Factor Extraction

Basic Concepts

The full principal component extraction model assumes that all the variance is common, and so the communalities are all equal to 1 (i.e. there is no specific variance). It is only when we reduce the number of factors that specific variance is introduced into the model.

In the principal axis factoring method, we make an initial estimate of the common variance in which the communalities are less than 1. This initial estimate assumes that the communality of each variable is equal to the square of the multiple regression coefficient for that variable with respect to the other variables. The principal axis factoring method is implemented by replacing the main diagonal of the correlation matrix (which consists of all ones) by these initial estimates of the communalities. The principal component approach is now applied to this revised version of the correlation matrix, as described in Factor Extraction.

Iterative Approach

In the principal axis method the following iterative approach is used:

R₀ = R, the original correlation matrix
R_p+1 = R_p with the main diagonal of R_p replaced by the communalities C_p of R_p

This algorithm is repeated until a predefined maximum number of iterations are performed or the communalities converge (and so there is too little difference between C_p and C_p+1 (and therefore between R_p and R_p+1. The final version of R_p is then used as in the principal component method of extraction.

We now discuss how to calculate the communalities C_p. To calculate the initial communalities C₀ for principal axis factoring we use the value of R² between each factor and all the other factors. For Example 1 of Factor Extraction, the initial communalities are given in range V33:V41 of Figure 1.

Figure 1 – Initial Communalities

Referring to the sample data in Figure 1 of Factor Analysis Example, the communality for the first factor (cell V33) can be computed by the formula =RSquare(B4:J123,U33), which has the same value as =RSquare(C4:J123,B4:B123), and similarly for the other eight factors.

It turns out that the vector of initial communalities V33:V41 can also be computed by the array formula

=1–1/DIAG(MINVERSE(M4:U12))

where M4:U12 is the correlation matrix (see Figure 3 of Factor Analysis Example).

For each p we show how to compute the communalities C_p+1 in the next example.

Example

Example 1: Repeat the factor analysis on the data in Example 1 of Factor Extraction using the principal axis factoring method.

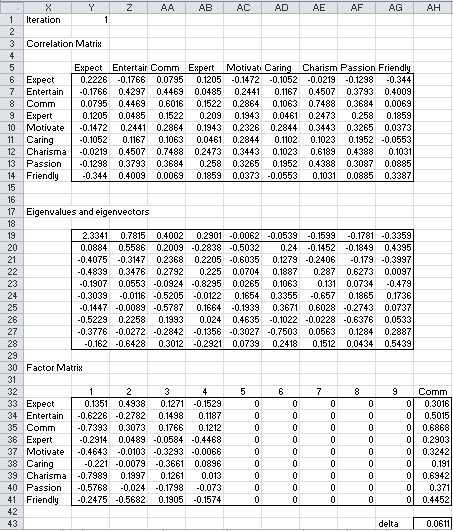
As calculate the correlation matrix and then the initial communalities as described above. We next substitute the initial communalities in the main diagonal of the correlation matrix and calculate the factor matrix as we did in the principal component method of extraction. This is shown in Figure 2.

Figure 2 – Iteration #1

The revised correlation matrix R₁ in range Y6:AG14 is equal to the original correlation matrix with the entries in the main diagonal replaced by the communalities calculated in the previous step (i.e C₀ in this case). We can calculate this correlation via the array formula

=M4:U12–IDENTITY()+DIAGONAL(V33:V41)

where M4:U12 is the original correlation matrix R₀ (Figure 3 of Factor Analysis Example) and V33:V41 are the communities C₀ (from Figure 1).

Eigenvalues and eigenvectors

The eigenvalues and eigenvectors in range Y18:AG28 is calculated by =eVECTORS(Y6;AG114). The Factor Matrix in range Y33;AG41 is calculated as in Principal Component extraction, except where the corresponding eigenvalues are not positive. While this is not possible for Principal Component extraction, it is possible for Principal Axis extraction. When an eigenvalue is non-positive (as is the case with the final 5 eigenvalues in Figure 2) the corresponding loading factors are set to zero. For example, the formula for calculating the first entry in the Factor Matrix (cell Y33) is

=IF(Y$19>0,Y20*SQRT(Y$19),0)

The new communalities C₁ (range AH33:AH41) is now computed as in Principal Component extraction. E.g. AH33 is computed by the formula =SUMSQ(Y33:AG33).

As explained above we next calculate C₂ and R₂ in the same manner and continue in this manner until a fixed number of predetermined iterations is reached (e.g. we will use p = 25 as the default maximum number of iterations) or until C_p and C_p+1 are sufficiently close. For this, we test whether the sum of the squares of the differences in the communalities is less than some predetermined precision amount (we will use .00001 as the default).

Iterations

For iteration #1 this metric is found in cell AH43 and is calculated by the formula

=SUMXMY2(AH33:AH41,V33:V41) 

(referring to Figure 1 and 2).

It turns out that after 19 iterations convergence goal of .00001 is reached with the difference between the communalities C₁₈ and C₁₉ of 8.81E-06. The values of the communalities after the 19^th iteration are given in range IP33:IP41 of Figure 3.

Figure 3 – Iteration #19

The Real Statistics Resource Pack provides an array function that automates the process of finding the converged values of the communalities, thus avoiding the tedious calculations described above.

Worksheet Function

Real Statistics Function: If R1 is a k × k correlation matrix then

ExtractCommunalities(R1, iter, prec, itere) = the 1 × k row vector with the communalities after convergence based on a precision value of prec but with a maximum number of iter iterations. As described above we use .00001 as the default value of prec and 25 as the default value of iter.

Since the eigenvalues and eigenvectors of the correlation matrix is calculated (using the eVECTORS worksheet function) in each iteration, a fourth argument itere can be used to specify the number of iterations used to calculate these eigenvalues/vectors (with a default of 100).

Once these values for the communalities are found, the Principal Axis extraction method proceeds exactly as for the Principal Component extraction method, except that these communalities are used instead of 1’s in the main diagonal of the correlation matrix. This is illustrated in Real Statistics Support for Factor Analysis.

References

Johnson, R. A., Wichern, D. W. (2007) Applied multivariate statistical analysis. 6th Ed. Pearson
https://www.webpages.uidaho.edu/~stevel/519/Applied%20Multivariate%20Statistical%20Analysis%20by%20Johnson%20and%20Wichern.pdf

Rencher, A.C., Christensen, W. F. (2012) Methods of multivariate analysis (3^nd Ed). Wiley