Overview
We use Box’s test to determine whether two or more covariance matrices are equal. Box’s test is a multivariate extension of Bartlett’s test for homogeneity of variance presented in Homogeneity of Variances.
Suppose that we have m independent populations and we want to test the null hypothesis that the population covariance matrices are all equal, i.e.
H0: Σ1 = Σ2 =⋯= Σm
Now suppose that S1, …, Sm are sample covariance matrices from the m populations where each Sj is based on nj independent observations each consisting of k × 1 column vector (or alternatively a 1 × k row vector).
Functions
Now define S as the pooled covariance matrix
where n = define the following:
![]()
The null hypothesis (of equal covariance matrices) is rejected when M(1 – c) > χ2-crit (or p-value < α).
This estimate works pretty well provided nj > 20, m ≤ 5, and k ≤ 5. A better estimate can be obtained using the F distribution by defining the following:
If c2 > c2 define F = F+, while if c2 < c2 define F = F–. Then F ~ F(df, df2). The null hypothesis is rejected if F > Fcrit.
Assumptions
If any of the Sj is not invertible then |Sj| = 0, and so ln|Sj| will be undefined. Thus M will be undefined and the test will fail.
Box’s test is sensitive to departures from normality. If the samples come from non-normal distributions, then Box’s test may simply be testing for non-normality.
Examples
Example 1: Determine whether the covariance matrices for Young, Middle, and Old are equal in Example 1 of ANOVA with Repeated Measures with One Between Subjects Factor and One Within Subjects Factor.
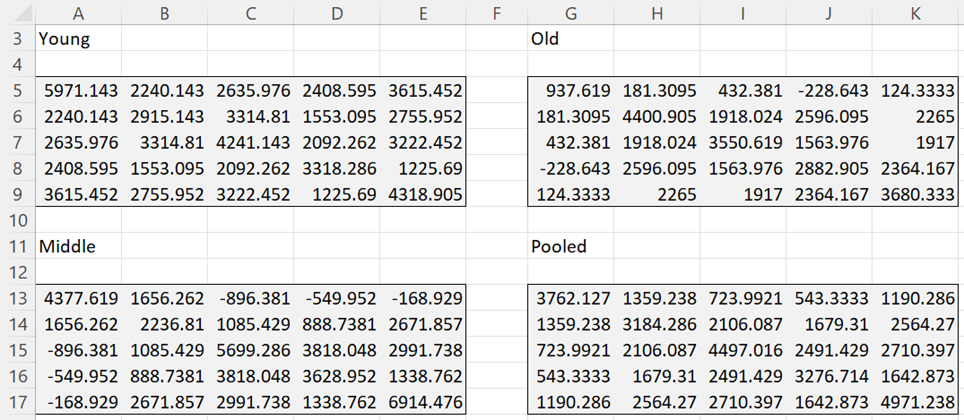
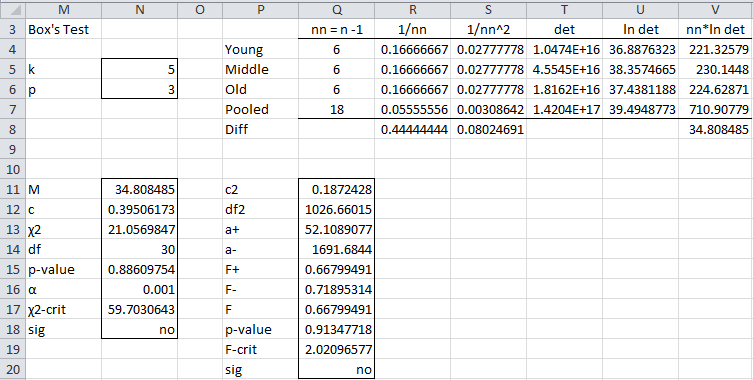
Figure 1 – Covariance matrices for Example 1
The sample covariance matrices for Young, Middle, and Old are calculated (see Figure 1) using the COV supplemental array function from the data in Figure 1 of ANOVA with Repeated Measures with One Between Subjects Factor and One Within Subjects Factor. Since the nj (j = 1, 2, 3) are all equal, the pooled covariance is simply the average of the Young, Middle, and Old covariance matrices.
The calculations required for Box’s test are given in Figure 2.
Figure 2 – Box’s test for Example 1
m = number of matrices = 3 (Young, Middle, Old), k = the size of each covariance matrix = 5 (each matrix is 5 × 5), n1 = n2 = n3= number of subjects in each sample = 7 and so n = n1 + n2 + n3 = 21. In columns Q, R, S and V, nn = n1 – 1 = 6 for Young, nn = n2 – 1 = 6 for Middle, nn = n3 – 1 = 6 for Old and nn = n – m = 18 for Pooled. The other entries are as described above.
Generally, we use a significant level of α = .001 for this test. From Figure 2 we see that M = 34.81 and both the chi-square test and the F test are not significant. We, therefore, have no reason to reject the null hypothesis that the three covariance matrices are equal.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
IBM (2017) Box’s M test. IBM SPSS Statistics Algorithms
Johnson, R. A., Wichern, D. W. (2007) Applied multivariate statistical analysis. 6th Ed. Pearson
https://educationexclusive.com/upload/pdf/Applied%20Multivariate%20Statistical%20Analysis%20by%20Johnson%20and%20Wichern.pdf
Rencher, A.C., Christensen, W. F. (2012) Methods of multivariate analysis (3nd Ed). Wiley
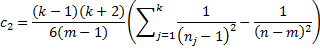
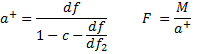
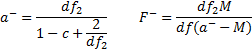
Hi Charles, I conducted a discriminant analysis, 5 variables, 2 groups, and a small sample size (n=44). The Box’s M result shows significant. May I know if I can ignore it due to the small sample or if I should use Pillai’s trace criterion? Thanks.
Hello Mikail,
If Box’s test is only a little significant, then I would probably ignore the result. Also, if the sample sizes of all the groups are about the same, then I would probably also ignore the result unless the p-value is very low. I would also check to see whether the data is normally distributed. If not, then Box’s test might be significant for this reason.
Some references that might be helpful:
https://paulogentil.com/pdf/MANOVA%20-%20Handout.pdf
https://docs.tibco.com/pub/stat/14.0.1/doc/html/UsersGuide/user-guide/discriminant-function-analysis-introductory-overview-assumptions.htm
Charles
Thanks for your explanation. BTW, do you suggest choosing the “Separate Groups” option for the covariance matrix while performing discriminant analysis in SPSS, since by doing so, the Box’s m test result became greater than 0.01 so there is no violation of this assumption.
I have 3 dv and three groups
I am getting a non significant Box M test but one of the levene’s test for univariate ANOVA is coming significant. How shall i interpret the result
It is not uncommon to get contradictory results. In the end, it is a judgement call as to whether the assumptions for a test are met.
Charles
Hello Charles,
I would appreciate you for some help with the analysis of the following data:
I have 16 varieties of a plant with 7 variables and 3 replicates (Let’s call them a, b, and c ). I have sample size=48 for each variable. I have performed a MANOVA and found that it was highly significant for Wilks. I would like to conduct a discriminant function analysis(DFA) and want your recommendations.
I would value your opinion very much, thank you!
Aqsa
Hello Aqsa,
DFA after MANOVA is generally a good approach.
Charles
Dear Charles,
I would like to conduct a discriminant function analysis using 6 variables and 3 groups with very little sample sizes (n1 = 13, n2 = 7, n3 =2). The major point in the analysis is to see, where group 3 is located concerning the 6 measured variables compared to groups 1 and 2. The LDFA’s results are fine, group separation and classification make sense and support visual assessment of the data – just Box-M is significant. Does that crash the whole LDFA or is there any way to rely on the results and report them anyway? And if so, how to justify the analysis despite the violation?
I would appreciate your opinion very much, thank you!
Eva
Hello Eva,
These are difficult questions to answer since the approach is usually not so clear-cut.
When the samples are roughly equal, then generally you don’t really need to use Box’s test. Your sample sizes are far from equal and so you should be careful. Even more concerning is that one of your samples only has 2 elements. I don’t really know how much you can rely on the results in this case.
In any event, I will pass on the advice from https://ncss-wpengine.netdna-ssl.com/wp-content/themes/ncss/pdf/Procedures/NCSS/Multivariate_Analysis_of_Variance-MANOVA.pdf
Homogeneity of Covariance Matrices
MANOVA makes the assumption that the within-cell (group) covariance matrices are equal. If the design is
balanced so that there is an equal number of observations in each cell, the robustness of the MANOVA tests is
guaranteed. If the design is unbalanced, you should test the equality of covariance matrices using Box’s M test. If
this test is significant at less than .001, there may be severe distortion in the alpha levels of the tests. You should
only use Pillai’s trace criterion in this situation.
Charles
Hello Charles,
I would appreciate some help with analysis of the following data:
I have 3 categories of patients (Let’s call them C1, C2, and C3). There are 13 subjects in C1, C2, & 21 in C3. The performance of each group was evaluated According to 3 parameters of visual function, let’s call them P1, P2, and P3. The dependent variables are all continuous measurements. I would like to know if 1 or more outcome parametersdiffers from the other(s) and, if so, which group differs is different. I performed a MANOVA and found that it was highly significant both Wilkes and Pillai. ANOVA was performed and Tukey HSD found highly significant differences between C1 & C3, and between C1 & C2, but no significant difference between C2 & C3. Unfortunately, Box’s test was highly significant Testing and found that it was highly significant(p= 2.51E-10). Can I still perform MANOVA + serial ANOVAs? If not, which test would you suggest?
Thanks again for all your help.
Joel
Hello Joel,
Given that you have different sample sizes, Box’s test may be relevant and so MANOVA results may be suspect. Pillai is the best of the tests to use in this case, but there is no guarantee. In any case, you don’t need Box’s test for ANOVA or Tukey’s HSD and this is really where you find out what you really want to know anyway. Since you are probably performing multiple Tukey’s HSD tests, you need the p-values to be very low to account for familywise error.
Charles
Thanks very much, Charles.
Could Levene test be used instead of Box’s?
Hi Joel,
For MANOVA with unequal sample sizes, you should use Box’s test. If you skip MANOVA and go to ANOVA then Levene’s test is sufficient. If Levene’s test fails then you can use Games-Howell follow instead of Tukey’s HSD.
Charles
Hi Charles,
Thanks very much for your help. A few points will help clarify your recommendations and determine the best analysis of the data.
1) Although the MANOVA was highly significant by both Pillai and Wilks, Box’s test was also highly significant at about p = 0.0001.
2) Per your suggestion, I therefore went straight to the ANOVAs for each of the 3 dependent variables. ANOVA for P3 was not significant, but ANOVAs for P1 and P2 were significant (p = 0.000002 and p = 0.000004, respectively). The Levene test for P1 and P2 were:
For P1, p= 0.0034 for mean, median, and trimmed mean.
For P2, p = 0.22 for mean, 0.34 for median, and 0.22 for trimmed mean.
Can I use Tukey for both, i.e. does Levene of 0.0034 for P1 rule out Tukey? Or should I use Games-Howell for both?
3) Results for Tukey and Games-Howell show similar results for both P1 & P2, with significant differences (before correction for multiple comparisons) between C1 & C3 and between C1 & C2, but not between C2 & C3 (for both P1 & P2). After correcting for multiple comparisons (3 paired comparisons for each ANOVA, the new level of significance becomes p = 0.05/3=0.167, is this correct?), above comparisons remain significant for both P1 & P2 with Tukey, but with Games-Howell, comparison between C1 & C2 is no longer significant (barely) for either P1 (p = 0.046) or P2 (p =0.028).
Should I stick with Games Howell and when reporting my results, should I cite results of Box’s test? Is there need to cite Levene’s if I use Games- Howell instead of Turkey?
Thanks again.
Joel
Hi Joel,
If the variances are unequal (per Levene’s test), then I suggest that you use Games-Howell. For P2 where Levene’s test shows equal variances, then you cam use Tukey’s HSD. Yes, in #3 you should stick with Games-Howell, but report that you are comparing with .0167 and the result is close.
Charles
Hi there,
I am doing a mixed repeated measure Anova. I have 2-time points (pre and post) and 3 condition group. Each of my condition group have (n=33, n=29, n=29). The Box’s M is significant at 0.000. Is there anyway to continue analysis the data with confidence? (e.g. using Pillai’s criteria?)
Thank you
Hello Masa,
Let me address this issue in a few different ways.
1. If I understand correctly, you have one repeated measures factor with two levels (pre and post) and one fixed factor with 3 levels. You can use the approach described on the following webpage. The epsilon correction should usually handle violations of sphericity.
One between subjects factor and one within subjects factor.
2. If you are using Box’s M test for MANOVA, you probably need to test whether 3 covariance matrices are equal (and not 6) since you need the covariance matrices for the three levels of the fixed factor versus the differences between the pre and post values (not the six combinations of pre and post with the 3 groups). In this case Box’s M test may not be significant.
3. Whether or not you need to do any of these tests depends on what specific hypotheses you want to test. If you aren’t interested in interactions between the two factors, then it may be sufficient to conduct one-way ANOVA with one factor with 3 levels based only on the differences between the post and pre values (i.e. the dependent variable is the difference between pre and post values). If significant then you can follow up with Tukey’s HSD.
4. Box’s M test is very susceptible to violations of normality, and so although it is supposed to test for equality of covariance matrices (an assumption for MANOVA) it may actually be showing that the multivariate normality assumption is violated. This may or may not be a big problem, although it is difficult to determine this.
Charles
Hi Charles,
Thanks for the response. I am not running a MONOVA but will be conducting several 3×2 ANOVAs to test my dependent variables. Some of my dependent variables are not highly correlated, so I am treating them independent from each other. I am trying to determine whether the 3 condition groups (teacher’s level of experience) impact the outcomes of an intervention (i.e. student’s level of well-being pre and post).
Does this mean for 2 way repeated measure ANOVAs I can ignore the BOX M value?
Thanks
Masa,
Yes, equal covariance matrices is not an assumption for 2-way repeated measures ANOVA, and so you don[t need to conduct Box’s M test.
Charles
Charles,
I would like to bring your attention on the discrepancies of the Box’s test results when I used the function BOX(R1, k) using the standard format vs covariance format for the input dataset range.
When I used covariance format data, the results are exactly the same as the ones presented in Figure 2. But with the standard input format, the results are as follow:
M stat 40.60989914
df1 30
df2 1397.398533
F stat 0.866218892
p-value 0.674877933
I have double-checked the input data range and individual values included in the dataset to ensure the accuracy of the data selection.
-Sun
Hello Sun,
Yes, you are correct. I need to research why the values are not consistent. I will correct this shortly and update the software.
Thank you for finding yet another error. As always, I appreciate your diligence in finding such mistakes.
Charles
Hi
I conducted a mixed ANOVA and Box’x test has been violated as well as some variables in Levene’s test (most of them are non-significant though). My total sample is 90, with 30 participant in each group (I have three groups) . how should I proceed ? Any references to back up my decision?
PS: My data is not normally distributed
Hi,
If det is -ve then Ln det won’t compute. Is it ok to use the absolute value of det in this case?
Chris,
It is unlikely that the determinant is negative, and so you should figure out why you got a negative value.
Charles
Hi Charles,
But is it wrong to assume the absolute value?
Hi Natan,
What absolute value are you referring to?
Charles
Hi Charles
I referrer to use the absolute value of a negative det, same case Chris reported above.
My question is, when eventually det is negative should I consider the absolute det value so I can comput Ln or should I consider 0 in calculation? Whats is more adequade or aproximate?
Thanks!
Natan
Hi Natan,
The determinant of a covariance matrix can’t be negative. If a negative value is returned, it is probably some value very close to zero (e.g. -1.3E-08). This value is negative due to round-off errors in Excel’s calculations and should be considered to be zero.
Charles
Charles,
I am currently doing my dissertation and I am running analysis on SPSS. I have 1 independent variable which is labelled group (control or experimental) and I have 2 types of DV: psychological markers of stress (baseline, post-intervention and post task) and physiological markers of stress HR/BP (baseline, post-intervention and post task). Therefore I am running a one-way MANOVA.
When I go to run this analysis I am getting the message: Warnings – Box’s Test of Equality of Covariance Matrices is not computed because there are fewer than two nonsingular cell covariance matrices.
I am not an expert with SPSS and I am in need of help, how can I move forward in this situation?
Many Thanks,
Emily
Emily,
Sorry, but I don’t use SPSS and so I don’t know the meaning of this message. It may be caused by having a small sample size, but I am not sure.
Charles
Charles, thanks for interesting material.
Do you know about an application of the Box’s M test concept to compare non-parametric rank correlations matrices? For instance, an ’emp’ matrix is the correlation matrix that contains correlations between the emprical values (time series), the ‘sim’ matrix is the correlation matrix — the simulated values. We need to test the null hypothesis H0: matrices ’emp’ and ‘sim’ are drawn from the same distribution.
Sem,
I don’t have any experience with this topic, but perhaps the following webpage will be of help to you:
https://stats.stackexchange.com/questions/280092/how-to-compare-of-two-spearman-correlations-matrices
Charles
I want to examine the relationship/effect of a 2-group qualitative IV, a numeric covariate, and their interaction on 7 numeric DVs. If I do seven hierarchical regressions or seven ANCOVAs, I get a combination of significant main effects and interactions for all of them. However, if I run a MANCOVA with all 7 DVs, the Box’s test comes back at .002. According to this page, that is problematic. I have seen other pages where only p < .001 is considered problematic. What should I do in this situation? I have seen some suggestions to use the Pillai's trace result. Is this correct? How can I move forward with this situation? Thank you in advance.
Thomas,
Sorry, but I would have to understand your situation in more detail to provide a credible answer. Unfortunately, I don’t have the time to delve more deeply into your situation. Perhaps someone else from the community can provide some insight.
Charles
Hiya, I have just conducted a Multivariate General Linear model test and in the Box Test the significance has come back at .000, i am just wondering does this mean that the finding is significant or not. I am very new to Spss (started using it yesterday and have been told to do my whole dissertation on it. Please can someone help me.
Thankyou,
Becca
Rebecca,
For the Box test, the usual significance level is alpha = .01 (whereas for most tests alpha = .05 is customarily used). Thus, if the p-value that you get from the test is .000 (i.e. zero to three significant digits), then clearly .000 < .01, and so you have a significant result. Charles
Dear Charles,
For my research project I want to examine whether adolescents (high versus low trait aggression and boys versus girls) differ in their preferences for different types of violent media content.
I have the following dependent variables (gathered through a content analysis of adolescents’ favorite television programs):
– overall aggression
– 3 subtypes of aggression (physical, verbal and indirect aggression)
– aggression in different contexts (graphic, realistic, humorous, rewarded, punished)
My data is not normally distributed. Therefore, I have considered testing non-parametrically. However, I would have to conduct so many separate Mann-Whitney tests I believe the loss of power would be insurmountable. So, I have returned to my original plan of testing my hypotheses with one two-way ANOVA (with overall aggression as the dependent variable and sex and trait aggression level as between-subjects factors) and two MANOVA’s (one with the three subtypes of aggression and one with all the context variables, both with sex and trait aggression level as between-subjects factors). Does this make sense?
If so, do I understand correctly that if the Levene’s test is not significant for all dependent variables the (M)ANOVA is robust enough to test the non normally distributed data with? Do I have to test the Levene’s test separately for the two factors? And what if Levene’s test is significant for some dependent variables? I have now tested it with both factors simultaneously (I don’t whether that is correct) but then three of my context variables are significant.
Thank you very much in advance.
Kind regards,
Amber
Amber,
1. I don’t really have enough information about your situation to be able to judge whether or not the approach that you are using makes sense.
2. Regarding the MANOVA assumptions, please see the following webpage:
https://real-statistics.com/multivariate-statistics/multivariate-analysis-of-variance-manova/manova-assumptions/
Charles
Hello Charles, Thank you for all the information!
I have conducted a Manova of 10 dependent variables between 2 groups. each group n=50.
Box’s M: F(55,31014)=2.175, p=0.000
What does it mean? I understand that the covariance is unequal. Does this invalidate the subsequent analysis?
Leven’s test of equality of error variances showed significance for 4 of the dependent variables.
do you have any recommendations/suggestions for me?
references for articles that can help?
Thank you for your time and help!
Shiran
The significant result for Box’s M test indicates that either the normality assumption fails of the equal covariance assumption fails. This could invalidate MANOVA. If the sample sizes across the groups are the same, then this is less of a problem and you should be able to use MANOVA anyway. I would then use the Pillai Trace.
When you say “between 2 groups” do you mean that you have two independent variables? If so you can use Hotelling’s T-square test, which is a special case of MANOVA. In this case, there is a version of the test when the covariance matrices are unequal. See the following webpage:
https://real-statistics.com/multivariate-statistics/hotellings-t-square-statistic/hotellings-t-square-unequal-covariance-matrices/
With so many dependent variables and so small a sample size, I would be concerned about the power of the test.
Charles
thank you very much for your answer!
I meant 1 independent variable (culture) with 2 groups (usa/russia).
is there anything else i can do for strengthening the results?
thank again!
shiran
Essentially this just means that you have dependent variables for USA and the same dependent variables for Russia (sic). It sounds like I am missing something. What are you trying to test?
Charles
I hope i can explain myself..
i’m looking for the differences between usa/russia participants regarding several statements. i’m assuming that russia will have a lower mean across all statements.
Hi,Charles
I have received a warning message:
Box’s Test of Equality of Covariance Matrices is not computed because there are fewer than two nonsingular cell covariance matrices.
What wrong and how can i deal with it ?
best,
Sirinna
Sirinna,
This sounds like an error message from SPSS. I am not familiar with the error messages from SPSS, SAS, etc. The website focuses on Excel.
Charles
Is there any way I could get access to the Excel file shown here?
Nevermind, just found it.
It means the group covariance matrix cannot be inverted–generally due to too small a number of element in the group.
Hi Michael,
Sorry, but I don’t know what your comment is referring to. Was this regarding an exchange from a long time ago?
Charles
Hello. I am very sorry but I don’t really understand a lot. I am doing Mixed-design ANOVA and my normality assumption is not met. And I have Levene’s test: p = 0,71 which means there is homogeneity of variances, right?
Do I have to check this Box’s test? SPSS automaticlly calculated it and p = 0,013. What does that mean? Is this data important for me?
Thank you very much!
Sincerly
LanaLo,
Yes, your interpretations of Levene’s and Box’s tests are correct. If you are conducting an ANOVA you really don’t need to use Box’s test; Levene’s test should be sufficient. Also note that Box’s test is very sensitive to normality; since your data is not normal it is not surprising that you can get a a significant Box’s test even though the homogeneity of variance is actually met.
Charles
Hello Charles,
I am conducting a research on advertising effectiveness, when studying gender interaction on the dependent variables (during MANOVA), i found that my box’s m test was significant. i have checked the normality of my data and found it normal. also, i have large and unequal sample sizes, so is it allowable in my case to proceed with manova even if box’s m was significant? further, i have also read that pillai’s criterion should be used if box”s m is significant instead of wiki’s but i was was unable to find any reference. please advice me on the matter and if possible provide me with a reference.
Regards
Danish,
You can proceed with MANOVA, but it is important to report the reservations you have based on Box’s M test.
Regarding which criteria to use, see Field, A. (2009) Discovering statistics using SPSS. 3rd Ed. SAGE. Other sources are
Olson, C.L. (1976) On choosing a test statistic in multivariate analysis of variance. Psychological Bulletin, 83, 579-586
Olson, C.L. (1979) Practical considerations in choosing a MANOVA test statistic. Psychological Bulletin, 86, 1350-1352
Steven, J.P. (1980) Power of the multivariate analysis of variance tests. Psychological Bulletin, 88, 728-737.
Charles
Hello Charles,
I have a design where there is one intergroup factor (2 levels) and one repeated measures factor (3 measures). I used to think, that for assumptions you must check both sphericity (Mauchley’s) and homogeneity of variances (Levene’s test). However, I was recently told that I could use M Box test for this. Which approach do you recommend?
Also – having read above that M Box is sensitive to non-normal data, can one try M Box, and if significant, check sphericity + homogeneity instead?
What about checking correlation of means*st.devs only – seems crude, is it used?
hello Artek,
Since Box’s M test is sensitive to non-normality, I tend not to use it. If you see that the data is normal, then I guess it is ok to use.
Usually I check for homogeneity of variances. I do this by comparing the sample variances (or using Levene’s test if I have any doubt). I then rely on the GG and HF sphericity correction factors. I have never tried to use the method you describe in your last paragraph.
Charles
Charles
Charles
I have conducted Shapiro-Wilk normality tests (passed) on data then used in a 2-Way Anova. I am aware that the study is underpowered, with only 7 participants each of three training groups. Box’s Test is contravened (p<0.05) with a significance of 0.034. Does this invalidate the subsequent results/analysis? Or should I be using p<0.01 for this test. If the latter should I not be using a similar p value for other tests (e.g. Levene's)?
Barry
Barry,
If you are performing 2-way Anova, I would use Levene’s test (instead of Box’s test) to check homogeneity of variances. In any case, the Box’s Test result is close to .05 and so is not too concerning.
Charles
Hi, could you please help, im doing my dissertation and ive performed a 2 factor manova but my box test is showing .000 sig? what shall i do? should i no longer use this test. Im trying to test the difference between divorced/intact families and the duration of both martial status.
Charlie,
Make sure that the problem isn’t due to outliers. You should check for univariate outliers and multivariate outliers (using Mahalanobis distances). If so, you could rerun the test without these outliers. In this case you should still report the existence of the outliers.
Box’s M test is quite sensitive to violations of normality. If you believe the test is giving a significant result because the data is not multivariate normally distributed, then results from MANOVA might still be valid (although it will likely be difficult to determine whether the problem is normality of homogeneity of covariance matrices).
Don’t use MANOVA, but use separate ANOVA tests instead. Not ideal, but it might be the best you can do.
Charles
Hi Charles
What does it mean when the Box’s M test is violated? Can you then perform Discriminant analysis anyways and just be aware of the it when you interpret your results?
Best,
Julie
Julie,
Violation of this test could mean that any results obtained from the test that depends in the assumption of equal covariance matrices is invalid. It really depends on by how much the covariance matrices are different.
A particular problem with Box’s M test is that a significant result may be due to a violation of normality and not equal covariance matrices. The specific test that you are using may be pretty robust to violations of normality but not heterogeneous covariance matrices (in fact this is usually the case).
Charles
Hi Charles
I don’t know how I can interpret Box’s test….. when it is significant, does it mean that our groups are not homogeneous? am I right?
Fatima,
Yes, you are correct. A significant result means that we reject the null hypothesis that the groups have equal covariance matrices.
Charles
Does this work for scalar observations (i.e. k = 1)?
Also, if I want to use a similar test to check for sameness of several regression coefficients, could I do it? Here’s what I want to do:
I have several models: “y = alpha + beta*x”, each based on n scalar observations. I want to use the above test, plugging in (k = 1) and replacing your S_j with alpha_j or beta_j (separate tests). Would that allow me to test the null hypothesis that all the true alpha’s or beta’s are the same?
Tim,
When there is only one independent variable Box’s M test is known as Bartlett’s test.
I have no reason to believe that you can use this test that the alpha or beta values are the same.
Charles
this is nice but what is the relationship b/n sample proportion Box’s test!
Sorry, but I don’t understand your question.
Charles
Hi there, I have received an error message:
Box’s test of equality of covariance is not computed because there are less than two nonempty cells.
Levene’s test of equality of error variances is not computed because there are less than two nonempty cells.
Can someone explain what this means, and what I should do please?
Liz
Liz,
It just means that you have too little data for these tests to be used. If you believe that you do indeed have more than two data elements then this probably means that you haven’t entered the arguments to these functions correctly.
Charles
In the “F-minus” equation, should the denominator read “(a-minus – df2)” instead of “(a-minus – M)”? The former agrees with the results in Fig.2 and the latter does not.
Todd,
It looks like the mistake is in Fig 2. I will fix the website and issue new versions of the software and the multivariate examples workbook.
Thanks for catching this error.
Charles