WLS regression via OLS regression through the origin

Basic Concepts

Suppose that we have data (x₁₁, …, x_1k, y₁), …, (x_n1, …, x_nk, y_n), where for each i, y_i is the mean value of y for all samples whose independent variables have the values x_i1, …, x_ik and σ_i is the standard deviation of these samples. Now we convert the usual linear regression

into the equivalent form

Since = var(y_i) = var(ε_i), it follows that var(ε_i/σ_i) = 1, and so the homogeneity of variance assumption (aka homoscedasticity) of this second model is met. This model has the form

The coefficients of this model can be found using an OLS model without intercept (here = 1/σ_i).

Example

Example 1: Repeat Example 1 of WLS Regression for Heteroskedasticity using the OLS regression through the origin approach. The example is as follows.

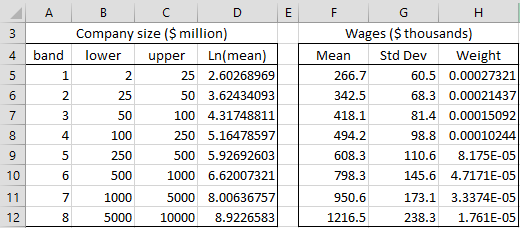
A survey was conducted to compile data about the relationship between CEO compensation and company size. The summarized data from 200 respondents is shown in Figure 1. Create a regression model for this data and use it to predict the wages of a CEO for a company whose annual revenue is $200 million a year.

Figure 1 – Relationship between company size and CEO compensation

We transform the OLS regression mode;

wages = b₀ + b₁ ∙ LN(mean company size)

into the following OLS regression through the origin form:

wages/stdev = b₀/stdev + b₁ ∙ LN(mean company size)/stdev

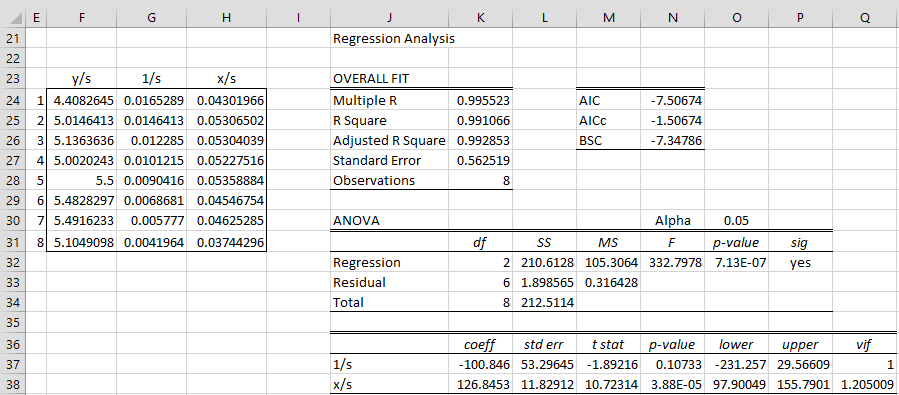
To do this, we transform the data from ranges D4:D12 and F4:G12 of Figure 1 to that shown in range F23:H31 of Figure 2. E.g. the values in cells F24, G24 and H24 are calculated respectively by the formulas =F5/G5, =1/G5 and =D5/G5.

Figure 2 – Dealing with heteroscedasticity using a model without intercept

We next use the Real Statistics Multiple Linear Regression data analysis tool with the without intercept option on the input data in range F23:H31, as described in Regression through the Origin, to obtain the regression analysis shown on the right side of Figure 2. This model takes the form

wages/stdev = -100.846 ∙ stdev + 126.8453 ∙ LN(mean company size)/stdev

or equivalently

wages = -100.846 + 126.8453 ∙ LN(mean company size)

which is the same as that calculated in Figure 2 of WLS Regression for Heteroskedasticity (although many of the other values in that figure are different).

Data Analysis Tool

Real Statistics Data Analysis Tool: The Weighted Linear Regression data analysis tool can also be used to perform WLS regression by using the OLS regression through the origin approach. To do this, just check the Use OLS regression through the origin option shown in Figure 1 of Real Statistics Support for WLS Regression.