Total Least Squares Regression

In Total Least Squares we describe total least squares (TLS) regression where there is one x variable. On this webpage, we briefly describe the multiple regression version.

Basic Overview

Suppose we have a sample of size m for n independent variables and one dependent variable. The key to finding the regression coefficients, in this case, is to use the Singular Value Decomposition (SVD) of the m × n+1 matrix A whose first n columns consist of the X data minus the means of each column and whose last column consists of the Y data minus the mean of the Y data.

The SVD of A takes the form A = UDV^T where U, D, and V are matrices with some special properties as described in Singular Value Decomposition. The Real Statistics Resource Pack provides worksheet functions SVD_U, SVD_D, and SVD_V that can be used to calculate U, D, and V in Excel.

In particular, the formula =SVD_V(R1, iter) calculates the n+1 × n+1 V matrix for the range R1 containing A. Here iter is the number of iterations used in the algorithm where iter defaults to 100.

It turns out that the estimated regression coefficient b_k for the x_k variable can be calculated as

where V = [v_ij]. The intercept regression coefficient is then given by

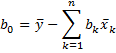
Example

Example 1: Find the regression coefficients using total least squares for Example 1 of Multiple Regression Least Squares (duplicated in Figure 1).

Figure 1 – Regression using TLS

Here, cells A15, B15, and C15 contain the means for the Color, Quality, and Price sample data. The resulting regression equation is Price = 5.731548 * Color + 4.409061 * Quality – 6.04619. The regression equation defined by ordinary least squares is  Price = 4.895288 * Color + 3.758415 * Quality + 1.751401.

Worksheet Function

Real Statistics Function: For an array or range R1 containing X values for k independent variables and R2 containing y values, we have the following array function.

TRegCoeff(R1, R2, iter) = k+1 × 1 column array consisting of the regression coefficients based on total linear regression using the data in R1 and R2. iter (default 100) is the number of iterations used to calculate the SVD decomposition.

For Example 1, the output from =TRegCoeff(A4:B14,C4:C18) is the same as shown in range F7:F9 of Figure 1.

Simple TLS Regression

The approach using SVD also works for the simple case where there is only one x variable.

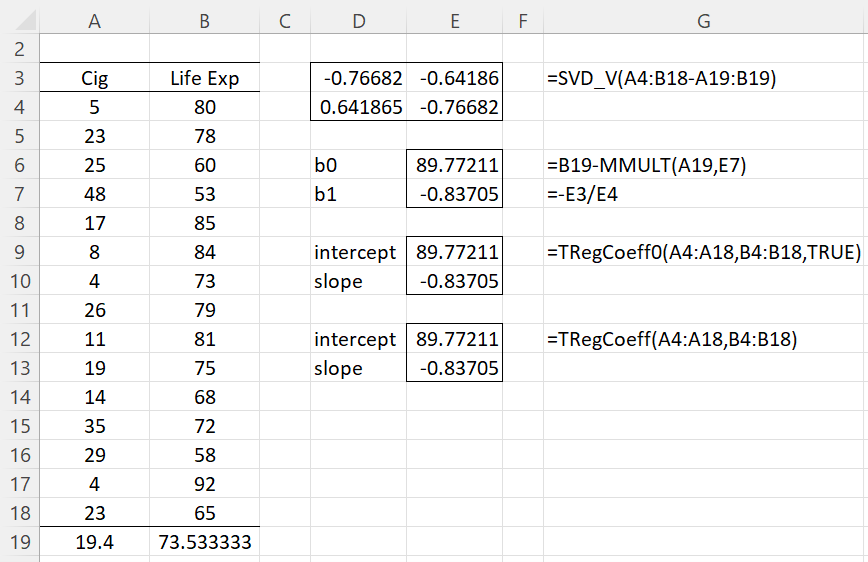
Example 2: Repeat Example 1 from Total Least Squares using the same approach used for Example 1.

The result is shown in Figure 2. Note that we obtain the same results as in Total Least Squares.

Figure 2 – Simple TLS Regression

Examples Workbook

Click here to download the Excel workbook with the examples described on this webpage.

Reference

Gavin, H. P. (2017) Total least squares. Duke University
http://people.duke.edu/~hpgavin/SystemID/CourseNotes/TotalLeastSquares.pdf