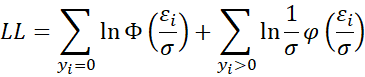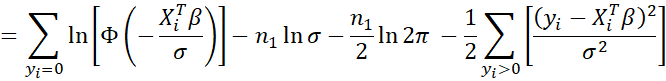Basic Concepts
The Tobit regression model (aka the censored regression model) is designed to model the linear relationship between independent variables (X) and a censored dependent variable (y). Censoring can occur from above (right) or below (left) or both.
For example, suppose we want to be able to predict the dividend of a stock based on the company’s earnings. Since the lowest dividend is zero, even for a company with poor earnings, the dividend will still be zero (censoring from below). Thus, the data for such companies hides useful information for such poor-performing companies.
A test used by the government measures pollutants in drinking water. The measuring device is only capable of measuring amounts up to 100 parts per million. Thus, pollutants above this value will report a value of 100. This is censoring from above.
Using ordinary linear regression will tend to distort the relationship between the variables. Tobit regression is used to provide a better estimate of the relationship.
Model description
Suppose that we have censoring from below at the value 0 (the standard situation). We define a latent variable y* as follows:
y* = XTβ + ε
where for any observations Xi = (xi0, …, xik) with xi0 = 1, yi* is the unobserved (latent) value of y (corresponding to the observed value yi), β = (β0, β1, …, βk) are the regression coefficients, and ε ∼ N(0, σ2). Now define
In a similar way we can have censoring from below (with lower limit a) and above (with upper limit b).
The regression model for y is the censored model and the regression model for y* is the uncensored model.
Assumptions
The Tobit model depends on the following assumptions (for consistency):
- Homogeneity of the variances (if heteroskedasticity)
- Normality of the residuals
Pdf and cdf for y*
The pdf of the distribution for y* is as follows:
where φ(z) = NORM.S.DIST(z, FALSE) is the pdf of the standard normal distribution and Φ(z) = NORM.S.DIST(z, TRUE) is the cdf.
The cdf is
Properties of the basic model
The basic Tobit model uses left censoring at zero.
If you require left censoring at a, then simply subtract a from the y values of your data. If you require right censoring at b, then replace all the y values of your data by b-y.
Property 1:
Expectations
We now present three different ways of looking at the expected value of censored normal data. Which of these is most relevant depends on the particular research being undertaken.
Property 2:
E[y*|X] = XTβ
Property 3:
E[y|y>0, X] = XTβ + σλ
where
Property 4:
Log-likelihood Function
The log-likelihood function for the Tobit model described above is
Our goal is to find the values of β = (β0, β1, …, βk) and σ that maximize LL. These will serve as our estimates of the Tobit regression coefficients. This is done using Newton’s iterative method wherein each iteration improves the estimate starting with a plausible initial guess. Convergence occurs when the difference between iterations yields little improvement. In general, iteration m+1 is obtained from iteration m as follows:
For Tobit regression, X is (β, σ) (and not the data in X which are viewed as constants), and f(β,σ) is LL viewed as a function of (β, σ). Finally, ∇f and H are the gradient and Hessian matrix, respectively, concepts from calculus, which we won’t go into further here. See Tobit Regression Technical Details for more information.
The square root of the elements on the main diagonal of H-1 (after convergence) serve as the standard errors of the regression coefficients.
References
Shanaev, S. (2021) Tobit model explained: censored regression (Excel)
https://www.youtube.com/watch?v=QS3OAYML2nM
Munk-Nielson, A. (2016) The Tobit model
https://www.youtube.com/watch?v=IwsE8Rr6l6E
Demeritt, J. (2024) Tobit model
https://jdemeritt.weebly.com/uploads/2/2/7/7/22771764/tobit1.pdf
Greene, William. 2003. Econometric Analysis. New Jersey: Prentice Hall.
Wikipedia (2024) Tobit model
https://en.wikipedia.org/wiki/Tobit_model
SAS (1999) Computing predicted values for a Tobit model
https://www.sfu.ca/sasdoc/sashtml/stat/chap36/sect24.htm
Olsen, R. J. (1978) Note on the uniqueness of the maximum likelihood estimator for the Tobit model
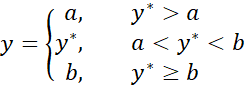
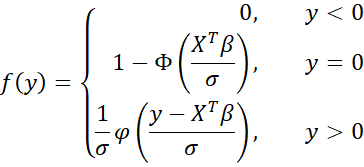
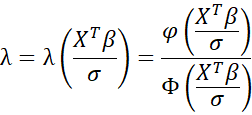
![E[y]](https://real-statistics.com/wp-content/uploads/2024/09/image045.png)