In ordinary regression, each of the variables may take values based on different scales. Sometimes it is useful to make the scales the same. This can be done by standardizing all the variables, or at least all the independent variables. The resulting regression coefficients are called the standardized regression coefficients.
Example
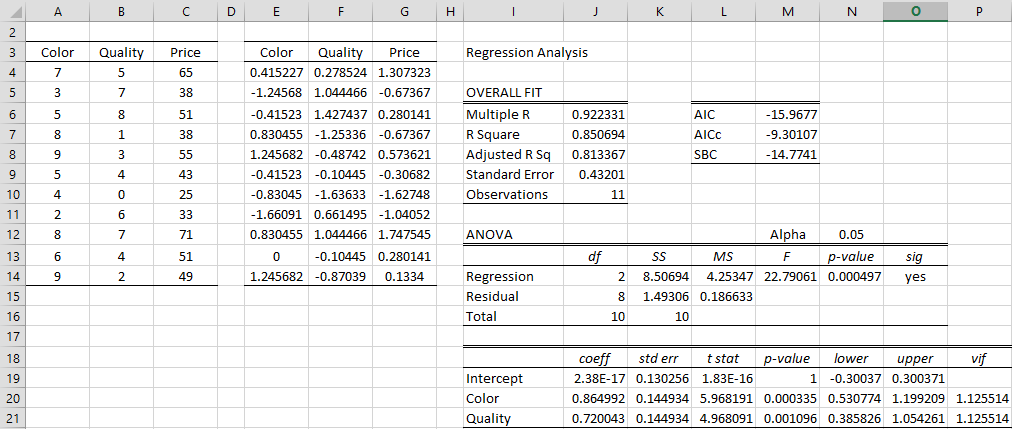
Example 1: Determine the standardized regression coefficients for the data in Example 1 of Multiple Regression in Excel (repeated in range A3:C14 of Figure 1).
Figure 1 – Standardized regression coefficients
We first standardize all the data, column by column, as shown in range E3:G14. E.g. the standardized Color values in range E4:E14 can be calculated by the array formula
=STANDARDIZE(A4:C14,AVERAGE(A4:C14),STDEV.S(A4:C14))
Alternatively, we can calculate all the values in range E4:G14 simultaneously, using the Real Statistics array formula =STDCOL(A4:C14), as defined below.
We now perform multiple linear regression to obtain the standardized regression coefficients shown in range J19:J21. Note that the intercept will always be zero and so we could have used regression without an intercept to obtain the same regression coefficients (although the standard errors will be slightly different). Note that the intercept won’t necessarily be zero if we don’t standardize the y data.
Conversion to unstandardized coefficients
Property 1: Suppose that the standardized regression coefficients are b0, b1, …, bk in the case where we don’t standardize the y data. Then the unstandardized regression coefficients are b′0, b′1, …, b′k where
Proof: Based on the premise, the following is true for all i
Property 2: Suppose that the standardized regression coefficients are b0, b1, …, bk in the case where we do standardize the y data. Then the unstandardized regression coefficients are b*0, b*1, …, b*k where
Proof: By Property 1, it follows that
where the b′j are as described in Property 1. Since the yi have been standardized, b′0 = 0, and so
from which the result follows.
Conclusion
Property 1 and 2 tell us how to calculate the unstandardized regression coefficients when the standardized coefficients are known. It follows from these properties that we can calculate the standardized regression coefficients when the unstandardized coefficients are known. This is summarized in Property 3 and 4.
Conversion to standardized coefficients
Property 3: Suppose that the unstandardized regression coefficients are b0, b1, …, bk in the case where we don’t standardize the y data. Then the standardized regression coefficients are b′0, b′1, …, b′k where
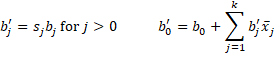 Property 4: Suppose that the unstandardized regression coefficients are b0, b1, …, bk in the case where we do standardize the y data. Then the standardized regression coefficients are b*0, b*1, …, b*k where
Property 4: Suppose that the unstandardized regression coefficients are b0, b1, …, bk in the case where we do standardize the y data. Then the standardized regression coefficients are b*0, b*1, …, b*k where
Observation: Since, by Property 3 of Expectation, Var(ax) = a2Var(x) where a is a constant, it follows that the standard deviation of a constant time x is the constant times the standard deviation of x. Thus, we can also calculate the standard errors of all the non-intercept coefficients described by these four properties. E.g. in the case described by Property 4, we see that the standard error of the standardized regression coefficient b*j for j > 0 is sj/sy times the standard error of bj.
Example
We can use Property 4 to calculate the values of the standardized regression coefficients shown in range J19:J21 and the standard errors in K20:K21 of Figure 1. This calculation is shown in Figure 2.
Figure 2 – Calculating standard regression coefficients directly
Here raw data from Figure 1 is repeated in range A3:C14. The means of each column are shown in row 16 and the standard deviations are shown in row 17. The ordinary regression coefficients and their standard errors, shown in range E3:G6, are copied from Figure 5 of Multiple Regression using Excel.
We can now calculate the standardized regression coefficients and their standard errors, as shown in range E9:G11, using the above formulas. E.g. the standard regression coefficient for Color (cell F10) can be calculated by the formula =F5*A17/C17. The standard error for this coefficient (cell G10) can be calculated by =G5*A17/C17.
Worksheet Functions
Real Statistics Functions: The Real Statistics Resource Pack provides the following functions that simplify the above calculations.
StdCol(R1) – returns an array with the same size and shape as R1, but with each column of data standardized.
StdRegCoeff(Rx, Ry, Rc, ystd) – returns a column array with the standardized regression coefficients for the x data in Rx and y data in the column range Ry based on the regression coefficients in the column range Rc (including an intercept coefficient). If ystd = TRUE (default), then standardized regression coefficients are based on the y data being standardized; otherwise the standardized regression coefficients are based on the y data in Ry not being standardized.
UnStdRegCoeff(Rx, Ry, Rc) – returns a column array with the unstandardized regression coefficients for the x data in Rx and y data in the column range Ry based on the standardized regression coefficients in the column range Rc (including an intercept coefficient). If the # of columns in Rx = the # of rows in Rc (i.e. Rc does not contain an intercept coefficient) then standardized regression coefficients are based on the y data also being standardized; while if Rc contains one more row than the # of columns in Rx the standardized regression coefficients are based on the y data in Ry not being standardized.
Note that Rx and Ry contain unstandardized data.
Referring to Figure 2, note that =StdRegCoeff(A4:B14,C4:C14,F4:F6) yields the results shown in range F9:F11 (except that now cell F9 has the value zero). Also the array formula =UnStdRegCoeff(A4:B14,C4:C14,F10:F11) yields the results shown in range F4:F6.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Stack Exchange (2017) How to convert standardized coefficients to unstandardized coefficients
https://stats.stackexchange.com/questions/30876/how-to-convert-standardized-coefficients-to-unstandardized-coefficients
Stack Exchange (2020) Convert standard coefficients to unstandardized (metric) coefficients for linear regression of a standardized independent variable
https://stats.stackexchange.com/questions/235057/convert-standardized-coefficients-to-unstandardized-metric-coefficients-for-li
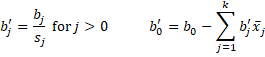



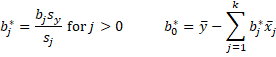


In case we have interaction terms in the equation, do you suggest standardizing by multiplying the standardized variables, or getting the product and then standardizing it?
And how do we de-standardize the coefficient for interaction term?
Priyana,
Generally, this is not necessary.
Charles
What isn’t necessary? Priyana asked multiple questions.
Hello Brandon,
I don’t think that the number of questions is the key criterion.
Charles
Dear Charles,
Are these 4 properties hold for the regression models without intercept term ?
Thank you!
James Li
Hello James,
There are two intercept terms: one for the standardized coefficients and one for the unstandardized coefficients. I haven’t gone through the details, but since these properties are probably only using algebra, the properties likely hold as long as one of the two intercepts doesn’t need to be zero.
Charles