Shapley-Owen Decomposition

Basic Concepts

When creating a multiple regression model, we would sometimes like to determine how much each independent variable contributes to the model. One way to do this is to decompose R-square using the Shapley-Owen Decomposition.

If x1, x2, …, xk represent the independent variable and y is the dependent variable, then the partial R-square for variable xj can be calculated by

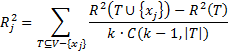
Shapley-Owen

where V = {x1, x2, …, xk} and |T| = the number of elements in some subset T of V. Also R2(T) = the R-square value for the regression of the independent variables in T on y. We assume that R2(Ø) = 0.

To calculate the R_j^2 when k = 16, we need to calculate R2 for 216 = 65,536 regression models. This number goes up to 1,048,576 if k = 20. Thus the approach is practical only when the number of independent variables doesn’t get too large.

Example

Example 1: Find the Shapley-Owen decomposition for the linear regression for the data in range A3:D8 of Figure 1.

Shapley-Owen decomposition

Figure 1 – Shapley-Owen Decomposition – part 1

We first calculate the R2 values of all subsets of {x1, x2, x3} on y, using the Real Statistics RSquare function. These values are shown in range G4:G11. We now apply the formula shown above for calculating R_j^2 for j = 1, 2, 3, as displayed in Figure 2.

Shapley-Owen decomposition 2

Figure 2 – Shapley-Owen Decomposition – part 2

Example Explanation

E.g. to calculate R_1^2, we first note that the subsets of V – {x1} are ø, {x2}, {x3}, {x2,x3}. as shown in range K4:K7). When x1 is included, these become {x1}, {x1,x2}, {x1,x3}, {x1,x2,x3}, as shown in range L4:L7. The R-square values corresponding to these subsets of independent variables are shown in ranges M4:M7 and N4:N7. The pairwise differences between these values are shown in the range O4:O7. The weights in range P4:P7 correspond to the denominator terms in the Shapley-Owen formula, namely k · C(k–1,|T|), where k = 3. Finally, the values in range Q4:Q7 are the pairwise products of the two terms to the left (e.g. Q4 contains the formula =O4*P4) and the value of R_1^2 is then displayed in cell Q8 using the formula =SUM(Q4:Q7).

We see that R_1^2, R_2^2, R_3^2 are .404979, .291195, .28995, which sum to .986125 (cell Q22), which, as we see from cell G11 of Figure 1, is the R-square value of the original regression, thus we have the desired decomposition. We see that variable x1 contributes the most to the R-square value (.404979/.986125 = 41.1%) and x3 contributes the least.

Worksheet Function

Real Statistics Function: The Real Statistics Resource Pack contains the following array function. Here R1 is an n × k  array containing the X sample data and R2 is an n × 1 array containing the Y sample data.

SHAPLEY(R1, R2): outputs an k × 1 column range containing the R_1^2, R_2^2, …, R_k^2 values

For Example 1, the output from the formula SHAPLEY(A4:C8,D4:D8) is shown in range G13:G15 of Figure 1.

Reference

Huettner, F. and Sunder, M. (2012) Stata module for decomposing goodness of fit according to Shapley and Owen values
https://www.stata.com/meeting/uk12/abstracts/materials/uk12_sunder.pdf

20 thoughts on “Shapley-Owen Decomposition”

  1. Hi Charles,

    Thank you for this. I manually replicated the results and completely grasped the concept of Shapley-Owen.

    I wonder if there are similar metrics for Logistic Regression? I know the concept of pseudo R-Squared in Logistic Regression differs from the R-Square in Linear Regression, but are there any metrics to evaluate the importance of each IV and capture their specific impact in Logistic Regression models?

    Reply

  2. Hi Charles,
    Thanks for making this available. However, I am still having problems with the array. I Visited your page for Array Formula and Functions but I did not get it well.
    How did you work the results for cell G8 with the formula “=RSquare(A4:B8, D4:D8). I keep getting an error.

    Reply

  3. Hi Charles, thank you for this. It has been invaluable in my understanding of Shapley-Owen.

    Can you provide a bit of advice? Let’s say I have eight independent variables, which is more than I can do in Excel by hand. How can I make this process more manageable?

    Reply

    • Hello Ralph,
      I don-t know of an easier approach to use when you want to make the calculations by hand. I have provided the Real Statistics function so that you can easily make the necessary calculation.
      Charles

      Reply

  4. Hello Charles,

    I want first to thank you for providing us this kind of statistics.
    As Henry already told you I don’t understand how to do without changing the data to have the results for the 2nd and the 3rd indicators.
    I don’t understand how to use in this case Array Formulas and Functions.
    Can you provide us an example (English is not my mother tong and it can be an explanation of my misunderstanding).

    Regards

    Reply

  5. Super useful, thanks for providing the examples and for creating the handy function. I noticed that the SHAPLEY function provides the Shapley result for the first column in the array (in your example A4:A8) but to get the results for the other columns (B4:B8 and C4:C8) I would need to rearrange the data array so that these columns come first. Is that correct or is there an easier way to indicate which column your referencing?

    Also, is there a max array size that can be used? I am running on an array that is 22 columns by 50 rows of data and it is taking a significant time to return a result.

    Reply

    • Hello Richard,
      The SHAPLEY function is what Excel calls an array function, and so it will return the values for all the columns. You can’t simply press the Enter key, however, when using it. See the following webpage for how to use an array function:
      Array Formulas and Functions
      The max array size is much larger than 20 x 50. I don’t know how long it will take to generate the answer.
      Charles

      Reply

  6. Sorry Charles, one more question – I’m a bit unclear about the weight column in your figure 2 excel example – I wasn’t clear how to translate k · C(k–1,|T|), into excel. From your numbers I noticed that the top/bottom rows were reproducible with 1/k and the middle rows 1/((k-1)*k). This worked for k=3 and k=4 but when I did k=5, the weights added to 1.1 so this does not seem to be the solution.
    Are you able to explain the weight column a bit more?

    Reply

    • Hello Henry,

      First of all, for the case under consideration where k = 3, T can have either 0, 1 or 2 elements. For 0 elements, k · C(k–1,|T|) = 3 · C(2,0) = 3, and so the weight is 1/3. For 1 element, k · C(k–1,|T|) = 3 · C(2,1) = 6 and so the weight is 1/6. For 2 elements, k · C(k–1,|T|) = 3 · C(2,2) = 3 and so the weight is 1/3. There are C(2,0) = 1 case with 0 elements, C(2,1) = 2 cases with 1 element and C(2,2) = 1 case with 2 elements. Thus the sum of the weights is 1(1/3) + 2(1/6) + 1(1/3) = 1.

      Now let’s look at the case where k = 5. T can have 0, 1, 2, 3 or 4 elements. The weights for each of these are the reciprocals of 5 · C(4,0) = 5, 5 · C(4,1) = 20, 5 · C(4,2) = 30, 5 · C(4,3) = 20, 5 · C(4,4) = 5, i.e. 1/5, 1/20, 1/30, 1/20 and 1/5. Assuming that variable 1 is under consideration, there is C(4,0) = 1 value of V with 0 elements, C(4,1) = 4 with 1 elements, C(4,2) =6 with 2 elements, C(4,3) = 4 with 3 elements and C(4,4) = 1 with 4 elements. Thus the sum of the weights = 1(1/5) + 4(1/20) + 6(1/30) + 4(1/20) + 1(1/5) = 1/5 + 1/5 + 1/5 + 1/5 + 1/5 = 1.

      Charles

      Reply

      • Thanks Charles,

        I got that working using this formula for the weight:
        1/(k*(fact(k-1)/(fact(n)*fact(k-1-n))))
        where k is the number of variables and n is the number of items in the w/o column.

        Reply

  7. Hi Charles,
    Thanks very much for making this available.
    I have been putting together a workbook to handle many independent variables and decided it was best to avoid copying the non-contiguous variable combinations due to the number of permutations. I thought it would be possible to use named ranges but I find they give different results.
    eg with your test data above – x1 against x3 R-sq = 0.849617
    but if I create a named range of the x1 and x3 data and use that in the formula I get 0.844964
    Do you know why the named range doesn’t work the same in the formula – is there no way to use that approach?

    Reply

    • Henry,
      The problem is not with using a named range. The problem is that the Real Statistics formula only recognizes a contiguous range. You can use the SelectCols array function to create a contiguous array and then use other Real Statistics functions on the result.
      Charles

      Reply

  8. Hi Charles,
    When I use the SHAPLEY function I recive as output only one number in one cell but not ther full range (in your example, only G13, but not G14 and G15).
    There is something that I do wrong?
    Thanks

    Reply

Leave a Comment