In Method of Least Squares for Multiple Regression, we review how to fit data to a straight line. Sometimes data fits better with a polynomial curve.
On this webpage, we explore how to construct polynomial regression models using standard Excel capabilities. Click here to learn more about Real Statistics capabilities that support polynomial regression.
Basic Concepts
We look at a quadratic model, although it is straightforward to extend this to any higher-order polynomial.
This is equivalent to the usual multiple regression model
studied in Multiple Regression Analysis where .
Quadratic Example
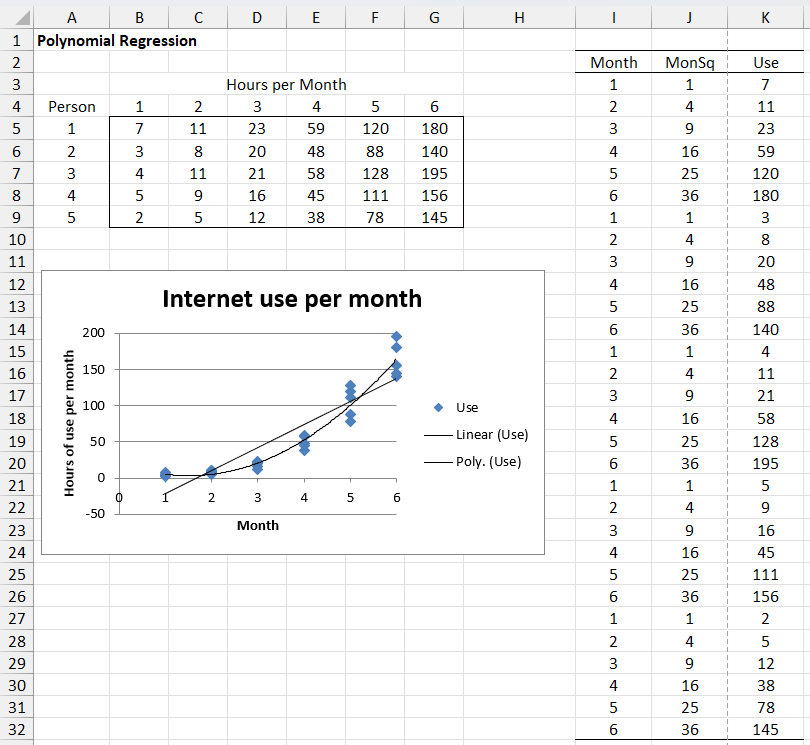
Example 1: A group of senior citizens who have never used the Internet before are given training. A sample of 5 people is chosen at random and the number of hours of Internet use is recorded for 6 months, as shown in the table on the upper left side of Figure 1. Determine whether a quadratic regression line is a good fit for the data.
Figure 1 – Data for polynomial regression in Example 1
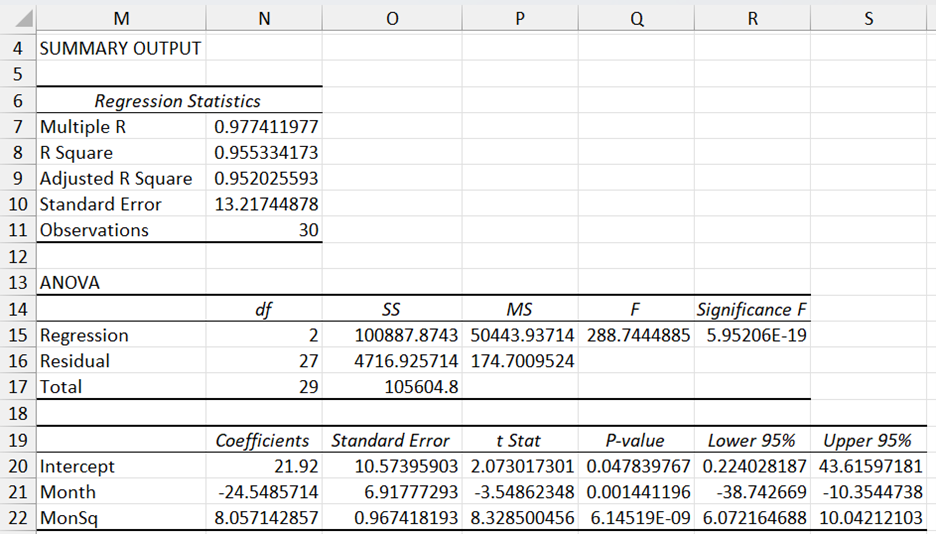
We next create the table on the right in Figure 1 from this data, adding a second independent variable (MonSq) which is equal to the square of the month. We now run the Regression data analysis tool using the table on the right (quadratic model) in columns I, J and K as the input. The results are displayed in Figure 2.
Results
Figure 2 – Quadratic regression output
The Adjusted R Square value of 95% and p-value (Significance F) close to 0 shows that the model is a good fit for the data. The fact that the p-value for the MonSq variable is near 0 also confirms that the quadratic coefficient is significant. This is further confirmed by looking at the scatter diagram in Figure 1, which shows that the quadratic trend line is a better bit for the data than the linear trend line. (To display the quadratic trend line select Layout > Analysis|Trendline and then More Trendline Options… On the display box which appears choose Polynomial trendline of Order 2.)
Figure 2 also shows that the regression quadratic that best fits the data is
Hours of Use = 21.92 – 24.55 * Month + 8.06 * Month2
Thus to predict the number of hours that a particular senior will use the Internet after 3 months, we plug 3 into the model (or use the TREND function) to get 20.8 hours of use.
Comparison with linear model
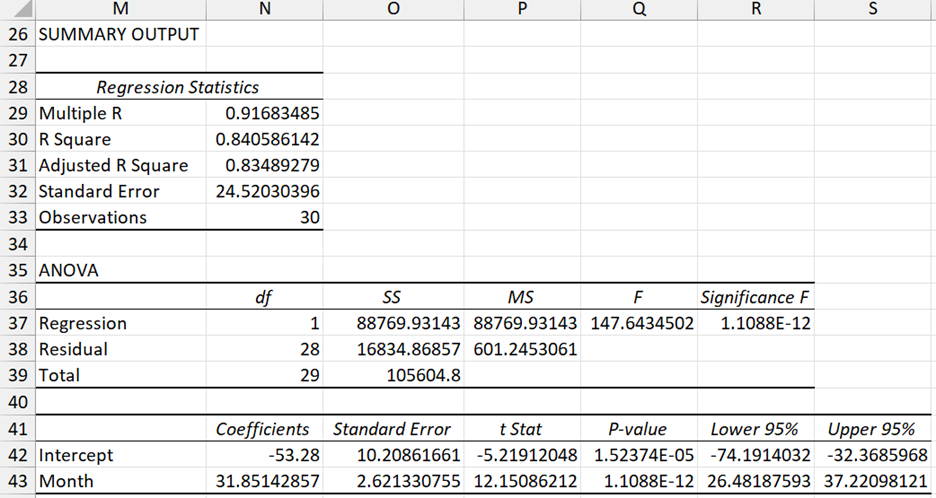
We can also run the Regression data analysis tool on the original data to compare the above results with the linear model studied in Regression Analysis. The linear model is generated by using only columns I and K from Figure 1. The output is shown in Figure 3.
Figure 3 – Linear regression output
That the quadratic model is a better fit for the data is apparent from the fact that the adjusted R-square value is higher (95.2% vs. 83.5%) and the standard error is lower (13.2 vs. 24.5).
Real Statistics Capabilities
Click here to learn more about Real Statistics capabilities that support polynomial regression.
Examples Workbook
Click here to download the Excel workbook with the examples described on this webpage.
References
Penn State (2025) Polynomial regression
https://online.stat.psu.edu/stat462/node/158/
Charles,
Is it possible to fix (or lock) one of the data points that lies on the x-axis, so that the quadratic regression is forced to go through that data point? In other words, force the regression to lie at a specified value on the x-axis (where y=0).
Terence
Hello Terence,
Suppose the specific value on the x-axis is 4 and we are doing linear regression. If you subtract 4 from the x values in your sample (without changing the y values), that seems to move your specific x value to 0. You can now perform linear regression through the origin, as described on the Real Statistics website.
I have to think about this further to see how this would work for quadratic regression.
BTW, do you know how to do quadratic regression through the origin?
Charles
What is the formula in excel to calculate correlation (R2) of quadratic/2nd order polynomial curve? I know y regression. I am searching for direct formula.
The approach described for a 2nd order polynomial regression is essentially linear regression using x^2 as if it were just another independent variable. In this case, the formular for R-square is the same as the formula for R-square for linear regression.
Charles
Firstly I am far from an expert in data analysis or the understanding of quadratic equations, but I successfully use Linest for a single polynomial regression curve to generate the values to be used in an Excel VBA formula.
Where I am completely stumped is whether this method can be used to predict the values from multiple X values?
I have the following table, and need to predict the resulting Y values based on the values in both axis. This needs to be done as a formula in VBA. Is this possible please?
Area
0.025 0.04 0.09 0.16 0.25
Vol 25 1.5
50 2.75 2.1
75 4.1 3.1 2
100 5.5 4.1 2.6 2 1.7
150 8.2 6.1 3.9 3 2.4
200 11 8.1 5.1 3.8 3.1
250 10.1 6.4 4.8 3.9
300 7.9 5.75 4.6
400 10.3 7.6 6.1
500 9.6 7.6
600 12 9.1
700 10.9
800 12.5
Andy,
Sorry, but I don’t understand your question nor your data.
Quadratic regression uses the equation y = ax^2 + bx + c. Are you looking for a regression of form y = ax^2 + bx + cz^2 + dz + e ?
Charles
Apologies Charles, the data all compressed when I hit enter!
Basically this is a small table with Area values along the columns, 0.025, through to 0.25, and volumes down the rows, 50 through to 800. All the other values are the results in the table, based on area and volume. Some of the cells were blank.
I know using Linest for a single set of data I can generate the figures to use in y = ax^2 + bx + c, but where I am lost is how to do the same for results based on two variables.
I hope this is clearer. As I said, this area is not a strength of mine.
Andy,
Are you looking for a regression of form y = ax^2 + bx + cz^2 + dz + e where x and z are the two independent variables?
Charles
Hi Charles,
What if I have 2 independent variables and one dependent variable, say example Q =output, L = Labor, K = Capital. So what formula should I be using and how to work on the excel?
Cher,
Do you want to include L^2, L^3, etc. as well as K^2, K^3, etc. How about L*K, L^2*K, L*K^2, L^2*K^2, etc.? As you can see, this can get pretty complicated, pretty fast. Also, with the addition of each term, you lose one degree of freedom, which may not be very desirable.
Charles
I want to measure purchase intent in response to a particular promotional scheme. For discussion purpose, I test 3 schemes – namely – Cash Discount (CD), Free Sample (FS) and Loyalty Programme (LP) and collected responses on a 5-point Likert scale (5 = Strongly agree (to buy) and 1 = Strongly disagree). How do I analyse this data? Can anyone please help me?
Shyam,
I cannot answer your question based on such a limited amount of information. Can you provide more information about the scenario that you are describing?
Charles
Dear Charles,
When the coefficient of x is significant, the coefficient of x ^ 2 is insignificant, or the coefficient of x is insignificant, the coefficient of x ^ 2 is significant, what kind of interpretation is it correct to make?
Sami,
It is possible for x and x^2 to be significant or neither to be significant. It is also possible that one is significant but not the other. E.g. if x and x^2 are the only independent variables and x^2 is significant and x is not, then x is not adding much to predicting y while x^2 is making a significant contribution.
Charles
Hello Charles,
Hope all is well at your end. A quick question, do you happen to know the formula to calculate the sum of squares for quadratic terms such as A^2, B^2? I am able to manually calulate first order main effects and interaction, but how would you calculate quadratic sum of squares?
The Excel function SUMSQ can be used for this purpose.
Charles
Hi Sir,
I want to do polynomial regression of order 3 and above with two independent variables. Can you help me with the procedure. I used to work on Excel but this software is new for me.
Thank you
Hello Abish,
The procedure is described on this webpage. What sort of questions do you have?
Charles
Hello sir,
Please tell me how to run the polynomial regression in excel if reciprocal of the variables are taken:
E.g; y=a+ b(1/x)+c(1/x^2) +d(1/x^3)
Gowher,
If you set z = 1/x then the equation takes the form y = a + bz + cz^2 + dz^3, which can be addressed by polynomial regression. Here your data comes from the reciprocals of the x data, plus the reciprocals of the x data squared and the x data cubed.
Note that this approach uses linear regression. You can also use non-linear regression as explained for exponential regression.
Charles
Thank you sir,
I have done as you suggest and the model is significant. Now please tell me how to obtain confidence limits of each predicted value that have been obtained from the above polynomial regression model in excel or in SPSS.
Dear Charles,
I am doing a multiple linear regression for four independent variables and one dependent variable. The independent variables are pH (x1), temperature (x2), time (x3), concentration of catalyst (x4), and the dependent variable is the % degradation (y) of the pollutant in water. I used the following second order polynomial to fit the experimental data that I have
y = b0 + b1*x1+b2*x2 + b3*x3 + b4*x4 + b5*x1^2+b6*x2^2 + b7*x3^2+b8*x4^2+ b9*x1x2+b10*x1x3+
b11*x1x4+b12*x2x3+b13*x2x4+b14*x3x4
My question is if this is a correct approach for fitting these experimental data. I used Excel for doing the fitting and my adjusted R square is 0.732 for this regression and the final p-values for all the remaining terms in the final equation are much less than 0.05. They are all statistically significant. Is it possible to give me advice on that?
Best,
Simon Sakhel
Simon,
It all seems reasonable. Does it agree with any previous results or your intuition?
Charles
Dear Charles,
I want to ask you about the experienced advantages and disadvantages of polynomial regression comparing with the linear regression, Especially for hydrologic modeling.
thank you.
Polynomial regression is just a form of linear regression where a power of one or more of the independent variables is added to the model.
I have no experience with hydrologic modeling, and so I can’t say whether this approach is useful.
Charles
Hello,
I have to find out relation between one dependent and four independent variables. I tried it with regression in excel. But I get the linear eqaution (linear regression). I would like to check whether polynomial or logarithmic or exponetial curve fits more correctly? I need this eqaution to predict for next entries. Also I dont want use the approach of using predicting equation and finding coefficient. That will not work out with me, as I have to repeat this procedure for multiple times.
Thank you in advance
Adish,
The procedure for polynomial regression is described on the referenced webpage. Exponential regression is described on the following webpage
Exponential Regression
As far as which approach fits better. One approach is to simply graph the data points and fit them with both an exponential trendline and a polynomial trendline (from Excel’s scatter chart capability) and visually see which one fits better. You can also calculate the SSE for each and see which is lower.
Charles
Hallo Charles,
I did not understand what you mean. I give example of my data,
Weight Height Age eyesight output
1 5 5 22 10
2 5 8 25 14
5 8 8 25 18
10 10 5 28 22
12 12 8 40 28
Now I have find equation fitting to this data so that , I can predict output for next values.
Here I am not sure, that equation will be linear or quadratic, polynomial. If nothing perfect which one gives least error.
Thanks
Adish
Adish,
I believe this is explained on the following webpage
https://real-statistics.com/multiple-regression/polynomial-regression/polynomial-regression-analysis-tool/
Charles
Hello Charles,
Thank you for your reply. But here are considering equatio will have only polynomial nature. I want to have flexibility with exponential or logarithmic curves too. Is it possible with your software?
Thanks
Adish
Adish,
If you want to mix polynomial and exponential factors, you can do it with the Real Statistics software, but you will need to manually format your data properly.
Charles
Hello Charles,
Also this link explains only one independent variable. In my case it is both multivariable and poynomial too?
Adish,
That is all that is covered in the website.
Charles
Hallo Charles,
Thank your for the reply.
I did not understand your comment. Is it possible multivariable and polynomial toghether regression with real statistics?
Adish,
Yes, using multiple linear regression, but you will need to manually transform some of the data.
Charles
Hi Charles,
Could you please explain, how to do multiple linear regression to generate multivariable polynomial regression? I tried but still not succeded.
Adish,
Suppose you have two independent variables x1 and x2 and want to consider polynomials of degree 3 or less, then the multiple linear regression model looks like
y = b0 + b1*x1 + b2*x1^2 + b3*x1^3 + b4*x2 + b5*x2^2 + b6*x2^3 + b7*x1*x2 + b8*x1*x2^2 + b9*x1^2*x2
Charles
Hallo Charles,
Thank you for your help.
So I have to predict equations and then manually enter x^2, x^3… ? right?
And then simple linear regresssion from excel data analysis option ?
Is there any other professional way? or excel built software for curve fiitng?
Thanks
Adish
Adish,
First you enter the data corresponding to the x values. Then you expand the data columns to get the x^2, x^3, etc. values. You can do this manually or by using Real Statistics’ Extracting Columns from a Data Range data analysis tool. Then you perform multiple linear regression — e.g. by using Real Statistics’ Multiple Linear Regression data analysis tool. The combination of these two data analysis tools streamlines the process. You can also use other tools such as SPSS, SAS, etc. to do this.
Charles
Hi where I can download this two analysis tool box from real statistics?
Data range data analysis tool
Multiple linear regression data analysis tool
Adish,
You can download all the data analysis tools from
https://real-statistics.com/free-download/real-statistics-resource-pack/
Charles
Dear Charles, how can I perform a quadratic regression with 3 dependent variables in excel? If yes how?
Thanks Lorenzo
Lorenzo,
The website doesn’t currently support multivariate regression (i.e. more than one dependent variable). This will be added some time in the future.
Charles
Hallo,
Did you add in your software?
Adish,
I don’t understand your question?
Charles
Support for multivariate regression as asked by Lorenzo ?
Hi charles,
I am using the polynomial regression formula to estimate the demand based on prices and demands given. How do I use the formula to find the standard deviation and mean, so I can find probabilities?
Nathan
Nathan,
The standard deviation and mean of what? Are you referring to forecasts or coefficients or something else?
Charles
Dear Charles, can explain to me why the third and fourth degree polynomial equations that I get from excel by changing a linear trend line to a polynomial of third and fourth degree do not match with the trend line and they result in outputs that are outside of the graph? Thanks in advance.
Ashebir,
If you send me an Excel file with your data and chart showing the trend line, I will try to answer your question.
You can find my email address at Contact Us.
Charles
Hi Charles,
The example above shows using a quadratic equation with one independent variable. Is it possible to use a quadratic or cubic equation with 2 or 3 independent variables? In that case how will the equation look?
Bhushan,
It can have many forms. E.g. y = b0 + b1*x1 + b2*x1^2 + b3*x1^3 + b4*x2^2 + b5*v1*x2.
Charles
Charles,
I beleive Bhushan is asking how to carry out this multivariate polynomial regression using your code. Currently the polynomial regression tab only allows for one dependent variable.
Chris,
I understood from his comment that he has multiple independent variables (not dependent variables). E.g. y = b0 + b1*x1 + b2*x1^2 + b3*x1^3 + b4*x2^2 + b5*v1*x2. In these cases you can use multiple linear regression where you treat terms such as x1^2 as a new independent variable y1 (whose value is x1^2).
Charles
Hi Charles,
Thank you for making this easier to understand – with the learnings from my statistics classes already blurred this was an excellent brush up!
I am trying to show if there can be talk of herding behaviour in stock markets. For this I have obtained market return data (r_m,t) to calculate the cross-sectional absolute deviation value. Now, in order for me to identify herding behaviour I have to detect a negative correlation between CSAD and r_m,t, from below formula (with D^event being a dummy for certain days):
CSAD_(m,t)=y_0+γ_1 D^Event |R_(m,t) |+γ_2 (1-D^Event )|R_(m,t) |+γ_3 D^Event R_(m,t)^2+γ_4 (1-D^Event )R_(m,t)^2+e_t
My question is now if you have any advise as to how I estimate these coefficients (y_3 and y_4 in particular) in excel.
Many thanks,
Maja
Sorry Maja, but I don’t understand the formula that you are using.
Charles
Hello Sir,
I want to ask about the application of polynomial regression.
I want to find a correlation between brain activities and enzyme activities during emotional state. So at first, I perform linear correlation/regression but almost all the results gave no significant in correlations (even though some are with large r) and I believe my variables are not correlated.
Then, if I use this polynomial regression to aim for that correlation, is it relevant.? Or what is the polynomial regression are actually aiming if it is not correlation?
Thank you,
Hayati
Hello
What is the p value for the polynomial line?
If I have a data series and I determine that the polynomial line is better fit than linear one and Rsquare is higher, how do I determine the p value for the polynomial line? do I have to change all my values to the square of the original values from the data series, run regression with excel and present the p I get?
Beck,
The referenced webpage describes how to calculate the p-value for the linear and quadratic coefficients of the polynomial regression model. There is one p-value for each coefficient (corresponding to the degree of the polynomial). There is one R-square value for the entire regression model.
Charles
Hey,
I want to do a polynomial model with four independent variables in software R. How can I go on about that?
Thanks
Sorry Varada, but this website is about statistics in Excel, not R. In fact, I don’t use R.
Charles
Thank you for this academic materials. Would you please give a guideline for analysis of third order polynomial regression model?
Regards
Shahadat
It is exactly as in Example 1 of the referenced webpage, except that now you must add another column with the cubes of the x values of the input data.
Charles
Dear Charles
Thank you for your response. Would you please illustrate the meaning of a fitted third order polynomial regression curve/model i.e. how I can explain it.
Regards
Shahadat
A fitted third order curve is one of the form y = ax^3 + bx^2 + cx + d. You are generally looking for the curve of this type that best fits the data. There are various versions of what best fit means. If you want to use linear regression then you are essentially viewing y = ax^3 + bx^2 + cx + d as a multiple linear regression model, where x^3, x^2 and x are the three independent variables. This is the approach used on the referenced webpage to find the best values of a, b, c and d. Here “best” means the smallest value of the sum of squared differences between the observed values of y_i and the values of y_i calculated when x_i is substituted for x in the equation y = ax^3 + bx^2 + cx + d.
You can also use a non-linear model to find the best values of a, b, c and d. This approach is illustrated on the following webpage (using Excel’s Solver):
https://real-statistics.com/regression/exponential-regression-models/exponential-regression-using-solver/
Charles
hie there i jus want to know if a transcendental model function be done in excel
What transcendental model functions are you referring to?
Charles
Hi Charles
I have a set of data (lets call em X and Y). I fit to them a quadratic regression and i get an R^2 = 99.29%. Now my problem is to estimate the error my new values produced by the fitted polynomial. To be more exact I am intersted to the point that the fitted curves crosses the x axis or in other words a*x^2 + b*x + c = 0. What is going to be the variance of this point ?
Hi
I am doing multiple regression and getting compile error in hidden module.
Please help.
Rishav Garg
Rishav,
To try to figure out what is happening, please answer the following questions:
1. What do you see when you enter the formula =VER() in any spreadsheet cell?
2. What do you see when you press Ctrl-m?
3. Which release of Excel and Windows are you using?
Charles
Hi Charles, would you be able to give guidance on a method within excel of applying ± 95% confidence limits to a 3rd order polynomial. The limits would then be used to control a process. Thank you in advance for your reply,
Paul,
For which variable are looking for a 95% confidence interval?
Charles
Hours of use per month, as in your example above.
Paul, I’m not sure that I understand what you mean by applying a ± 95% confidence limit. Generally, you should have more confidence in the accuracy of a statistic when its confidence interval is narrow. In particular if the confidence interval contains zero then the coefficient for that variable is not significantly different from zero, which means that that variable (at least the cube of that variable in this case) is not making a significant contribution to the regression model.
Charles
Hi Charles, Thanks for your response. I was hoping to plot a ±95% confidence interval about the polynomial trend. I understand the function when applying to linear regression, not so easy for polynomial I guess (=t*SYX*SQRT(1/n+(A18-XAVG)^2/SSX).
Paul,
Polynomial Regression is identical to multiple linear regression except that instead of independent variables like x1, x2, …, xn, you use the variables x, x^2, …, x^n. Thus, the formulas for confidence intervals for multiple linear regression also hold for polynomial regression. See the webpage Confidence Intervals for Multiple Regression.
Charles
Is the high collinearity (or correlation) between Month and Month^2 a concern?
Ryan,
The correlation between Month and Month^2 is .9789, which is quite high, but it is also not necessarily at the level of collinearity. If you perform regression with Month and Month^2, the result won’t be very different from the result with just Month^2.
Charles
So in that case, you would probably remove Month from the model and fit a new model using only Month^2 as your explanatory variable? My question is about the worrisome correlation between two independent variables in the model.
Thank you for your work.t
Linus