Regression through Origin in Excel

Excel Capabilities

The following Excel functions, described previously in Multiple Regression Analysis in Excel, can be used for regression without an intercept when the con argument is set to FALSE (con = TRUE is the default).

TREND(R1, R2, R3, con) = array function which predicts the y values corresponding to the x values in R3 based on the regression line based on the x values stored in array R2 and y values stored in array R1. If R3 is omitted it defaults to the range R2.

LINEST(R1, R2, con, TRUE) = array function which outputs a 5 × k range where k = the number of independent variables (plus 1 if con = TRUE), as described Multiple Regression Analysis in Excel.

Excel’s Regression data analysis tool, as described in Multiple Regression Analysis in Excel, you can force the constant term to be zero by checking the Constant is Zero option.

Real Statistics Functions

Real Statistics Functions: The following Real Statistics functions, described in Real Statistics Capabilities for Multiple Regression, can be used for regression without an intercept when the con argument is set to FALSE (con = TRUE is the default).

In the following R1 is an n × k array containing the X sample data and R2 is an n × 1 array containing the y sample data.

SSRes(R1, R2, con) = SSRes dfRes(R1, R2, con) = dfRes MSRes(R1, R2, con) = MSRes
SSReg(R1, R2, con) = SSReg dfReg(R1, R2, con) = dfReg MSReg(R1, R2, con) = MSReg
SSRegTot(R1, R2, con) = SST dfRegTot(R1, R2, con) = dfT MSRegTot(R1, R2, con) = MST
MultipleR(R1, R2, con) = R RSquare(R1, R2, con) = R2  AdjRSquare(R1, R2, con) = Adjusted R2
RegSE(R1, R2, con) = standard error REGF(R1, R2, con) = F-stat RegTEST(R1, R2, con) =  p-value

HAT(R1, con) = n × n  hat matrix

LEVERAGE(R1, con) = column range which contains the diagonal elements of the hat matrix

RegCoeff(R1, R2, con) = k × 2 range consisting of the regression coefficient vector  followed by a vector of standard errors of these coefficients if con = FALSE (the output is a k+1 × 2 range if con = TRUE, to include the intercept coefficient and its standard error)

RegY(R1, R2, con) = n × 1 vector of predicted values for y values in R2

RegE(R1, R2, con) = n × 1 residuals vector  for y values in R2

RegAIC(R1, R2, con, aug) = Akaike’s Information Criterion (AIC)

RegAICc(R1, R2, con, aug) = corrected Akaike’s Information Criterion (AICc)

RegSBC(R1, R2, con, aug) = Schwarz Bayesian Criterion (SBC)

The second argument R2 in the dfRes, dfReg and dfTot are optional (actually, this argument is not used).

Comparison with Regression with Intercept

In the case of regression without an intercept, the values of various statistics such as AIC, AICc, SBC, VIF, Tolerance, Cook’s D, DFFITS, etc. are the same as for multiple linear regression with an intercept, except that the definitions given in Multiple Regression without Intercept of dfRes, SSRes, correlation vector B, hat matrix H, R2, etc. are used and whenever k appears it is replaced by k – 1.

More Real Statistics Capabilities

Real Statistics Data Analysis Tool: The Linear Regression data analysis tool described in Real Statistics Capabilities for Multiple Regression has an option to perform regression without an intercept, as described in the next example.

Example 1: Repeat Example 2 of Multiple Regression Analysis in Excel using a linear regression model without intercept (see Figure 1 for a copy of the data)

Enter Ctrl-m and select Multiple Linear Regression from the Reg tab (or double-click on the Regression option and select Linear Regression if using the original user interface). Next, fill in the dialog box that appears as shown in Figure 2 of Real Statistics Capabilities for Multiple Regression, except that this time you need to uncheck the Include constant (intercept) option. When you click on the OK button the output shown in Figure 1 appears.

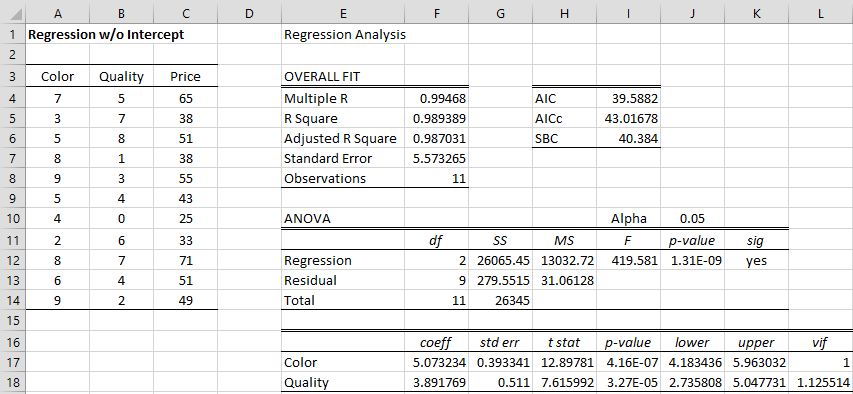
Multiple regression without constant

Figure 1 – Linear regression without an intercept

Note that the range F17:G18 contains the array worksheet formula =RegCoeff(A4:B14,C4:C14,FALSE) and cell F6 contains the formula =1-(1-F5)*F8/(F8-F12), although we could have used the formula =AdjRSquare(A4:B14,C4:C14,FALSE) instead.

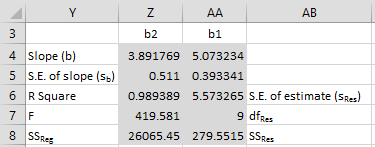
We could also use the array formula =LINEST(C4:C14,A4:B14,FALSE,TRUE) to calculate key values in the linear regression without intercept, as shown in Figure 2 (the labels have been added manually).

LINEST function without intercept

Figure 2 – Use of LINEST function

More Examples

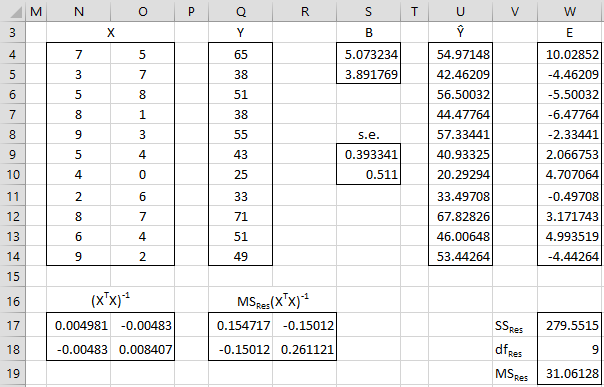
Example 2: Calculate the linear regression coefficients for the data in Example 1 using matrix techniques.

We use the same approach as in Multiple Regression using Matrices, with the modifications described in Multiple Regression without Intercept. The result is shown in Figure 3.

Regression without intercept matrices

Figure 3 – Matrix approach to linear regression without an intercept

Observation

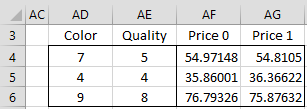
As shown in Figure 3 of Real Statistics Capabilities for Multiple Regression, when we perform linear regression with an intercept on the data in Figure 1, it turns out that the intercept coefficient is not significantly different from zero (p-value = .808). Thus it isn’t too surprising that predictions based on the models with and without an intercept won’t be very different. We can see this in Figure 4.

Regression forecast comparisons

Figure 4 – Comparison of forecasts

Here, the forecasted price using the model with intercept (Price 1) is compared with the forecasted price using the model without intercept (Price 0) for three diamonds. E.g. the price of a diamond with color and quality of 4 is estimated to be 35.86 based on the non-intercept model and 36.37 based on the model with intercept.

Reference

Eisenhauer, J. G. (2003) Regression through the origin. Teaching Statistics. Volume 25, Number 3.
http://web.ist.utl.pt/~ist11038/compute/errtheory/,regression/regrthroughorigin.pdf

16 thoughts on “Regression through Origin in Excel”

  1. Hello Charles,

    is it appropriate to use multiple regression through the origin in this fashion:

    y[t] = b1*x1[t]+b2*x2[t]+b3*x3[t] ..

    where x[t] are index variables and y[t] is their total/or average?

    What would be the interpretation of the coefficients?
    Is it sensible to draw any inference from the results?

    Thanks

    Reply

  2. The expression “with / without intercept” is confusing. Of course there is always an intercept. The intercept is either estimated or stipulated. estimated is the default. When the intercept is stipulated,R2 is computed differently in the graphics than in the analysis pack regression module, without explanation and both have as different meaning than when intercept is estimated. Let y be the indep vbl with mean y*, let y^ be the regression estimate based on x. let SS = sum(yi-y*)^2; SSR = sum(yi^ – y*)^2; SSres = sum(yi-yi^)^2. If the intercept is estimated then SS = SSR + SSres, and R2 = SSR/SS = 1-SSresid/SS. R2 has the clear meaning as % explained variance. If the intercept is stipulated, then SS# = sum(yi^2), SSR# = sum((yi^)^2) and R2 = SSR#/SS#, which may obviously be > 1. In the graphics, R2 = 1-SSres/SS which of course can be negative. To a mathematician this is utter lunacy. And of course no explanation is given.

    My question: if the intercept is stipulated, how is adjR2 calculated?

    Reply

    • Hello Roger,

      I agree with your comments. What specific changes do you suggest that I make to the website and Real Statistics software?

      AdjRSquare = 1 – (1 – RSquare(xarray, yarray, False)) * m / (m – n) where m = # of data elements (i.e. # of rows in xarray), n = # of independent variables (i.e. # of columns in xarray) and RSquare is as calculated by Excel’s LinEst(yarray, xarray, False, True) formula.

      Charles

      Reply

  3. Hello, Charles!
    How to calculate standard error for independant variables? When I used STDEV.S/SQRT(n) formula the number I got was different, than what I see in the table from Real Statistics and what excel calculated on its own. It means that there’s something wrong with the formula I’m using.
    What formula should be to calculate standard error in excel manually (so that it’s the same as in tables I get automatically)

    With appreciations to your site and work,
    Evgeniya

    Reply

    • Hello Evgeniya,
      The formula is STDEV.S(R1)/SQRT(COUNT(R1)) where R1 is the range containing the data.
      But the standard error for regression coefficients is calculated in a different way. What specific standard error are you trying to calculate? How does it pertain to regression through the origin (the subject of this webpage)?
      Charles

      Reply

      • Charles,
        thanks a lot for your quick reply!
        I’m trying to calculate each parametr of a regression manually on my own to create a list with a lot of formulas to make quick analyses all at once when i insert data. So now I’m stuck at calculating coefficients’ errors in a regression model.
        Searching for the answser in the Internet I have found only one formula that I wrote before, that doesn’t work as it turned out to be.
        What is the formula I need for regression coefficients?
        On this webpage you show detailed calculations, but haven’t found what looking for.
        Evgeniya

        Reply

    • I believe that con = TRUE is the real default. Try using the following data:
      x = 0, 1, 2, 3 and y = 5, 6, 7, 8. You’ll see that the regression doesn’t go through the origin.
      Charles

      Reply

  5. Sir,i want to predict diesel engine performance, by using eq.in the form as,Torque,T=(a1R+a2R^2+a3R^3)+(a4R+a5R^2+a6R^3)*Z+(a7R+a8R^2+a9R^3)*Z^2, here i want to find 9 coeff.with 30 data set ofT,Z&R.tnx

    Reply

Leave a Comment