Multiple Regression without Intercept

There are some problems where based on theoretical grounds we expect that the appropriate model is multiple regression without a constant term, i.e.

which is the usual multiple regression model where β₀ = 0. In the case with just one independent variable, this is equivalent to finding the line through the origin which best fits the data.

On this webpage, we explain the theory of this model. See Regression w/o Constant in Excel for a description of various Excel and Real Statistics capabilities for such models.

For the sample {y₁, y₂, …, y_n} of size n for the dependent variable y and samples {x_1j, x_2j, …, x_nj} for each of the independent variables x_j for j = 1, …, k, we let Y be the n × 1 column vector with the entries y₁, …, y_n and X be the n × k matrix [x_ij].

Most of the properties for ordinary multiple regression still hold where the design matrix is replaced by the matrix X = [x_ij], i.e. we don’t add columns consisting of ones. In particular, the regression coefficients for the least-squares model can be expressed by

It also turns out that B = [b_j] is the k × 1 column vector such that

We can use the Y-hat k × 1 column vector with entries

to express the least-squares model as

where H is the n × n  hat matrix

For ordinary multiple regression (including an intercept), we have

As we saw in Multiple Regression in Excel, SS_T = SS_Reg + SS_Res. To see this, first, note that

By taking the sum of both sides of the equation over all values of i and then squaring both sides, we get

The desired result follows since

which follows by substituting β₀ + β₁x₁ + … + β_kx_k for ŷ_i and simplifying.

These results don’t hold in the case where there is no constant term in the regression equation. Instead of fitting a line through the mean values, we need to instead fit the line through the origin. Since

It follows that

But

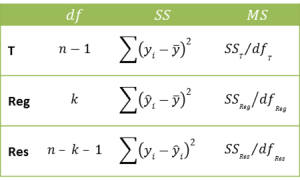
Thus, for regression without a constant term, we still have SS_T = SS_Reg + SS_Res and df_T = df_Reg + df_Res where

Using these new definitions, we define

Another version of R² is

For multiple regression including the constant term, these definitions are equivalent. This is not necessarily the case when the intercept is not included in the model. It is also not necessarily the case that the sum of the squared errors is zero (as for regression that includes a constant).

The adjusted version of R² is

Observation: It is important to note that the R² value for regression with an intercept is not comparable with the R² value for regression without an intercept (i.e. with an intercept whose value is zero). Thus if R² = .95 for regression without an intercept and R² = .80 for regression with an intercept, it doesn’t follow that the model without an intercept is a better fit for the data.

Observation: In general, it is better not to assume that the intercept is zero. In fact, as mentioned earlier, the only time you should use this type of model is when on theoretical grounds you expect that the intercept is zero. Some examples of this are:

• Hubble model for the expansion of the universe: galaxy speed = β ∙ distance from the earth
• Examples from Finance such as Capital asset pricing model (CAPM) and Cobb-Douglas production function

In the Hubble model example, there is no constant term since at time zero, according to the Big Bang Theory, all the matter in the universe is concentrated at a single point in space.

Of course, you can always use a regression model that includes the constant term, and check whether this term is significantly different from zero.

See Regression w/o Constant in Excel for a description of various Excel and Real Statistics functions and data analysis tools for creating multiple regression models without an intercept.